Матрицы и действия над ними. Обратная матрица
Матрицей называется прямоугольная таблица, содержащая  чисел, имеющая чисел, имеющая  строк и строк и  столбцов. Она обозначается столбцов. Она обозначается
 . .
Числа  называются элементами матрицы. Коротко эту матрицу обозначают так: называются элементами матрицы. Коротко эту матрицу обозначают так:  . Здесь . Здесь 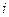 – номер строки, – номер строки,  – номер столбца элемента – номер столбца элемента  . Матрицу иногда обозначают и так: . Матрицу иногда обозначают и так:
 . .
Если столбцы матрицы сделать строками с теми же номерами, то полученная матрица называется транспонированной и обозначается
 . .
Если в матрице число строк и число столбцов совпадают, то матрица называется квадратной:
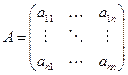 . .
Элементы  образуют главную диагональ матрицы. Число образуют главную диагональ матрицы. Число  называется порядком матрицы. Квадратной матрице можно поставить в соответствие число, называемое определителем матрицы, обозначаемое называется порядком матрицы. Квадратной матрице можно поставить в соответствие число, называемое определителем матрицы, обозначаемое  и равное и равное
 . .
Матрица, у которой все элементы главной диагонали равны 1, а все остальные элементы равны 0, называется единичной и обозначается
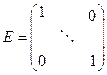 . .
Матрица, состоящая из одной строки, называется строчной и обозначается  . Матрица, состоящая из одного столбца, называется столбцевой, например, . Матрица, состоящая из одного столбца, называется столбцевой, например,
 . .
Пусть даны две матрицы с одинаковым числом строк и столбцов: 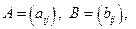 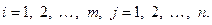 Эти матрицы называются равными друг другу (при этом пишут Эти матрицы называются равными друг другу (при этом пишут  или или  ), если все их соответствующие элементы равны друг другу, т. е. ), если все их соответствующие элементы равны друг другу, т. е.  для всех для всех 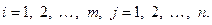
Суммой матриц  и и  называется матрица, обозначаемая называется матрица, обозначаемая  , элементы которой , элементы которой  для всех значений для всех значений  . Это правило можно записать так: . Это правило можно записать так:  . Аналогично вводится понятие разности двух матриц. . Аналогично вводится понятие разности двух матриц.
Произведением матрицы  на число l называется матрица, обозначаемая на число l называется матрица, обозначаемая  , элементы которой равны произведениям числа l на соответствующие элементы матрицы , элементы которой равны произведениям числа l на соответствующие элементы матрицы  , т. е. , т. е. 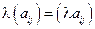 . Иначе говоря, чтобы умножить матрицу на число l, нужно умножить на это число каждый её элемент (для сравнения заметим, что для умножения определителя на число нужно умножить на это число все элементы какого-либо ряда). . Иначе говоря, чтобы умножить матрицу на число l, нужно умножить на это число каждый её элемент (для сравнения заметим, что для умножения определителя на число нужно умножить на это число все элементы какого-либо ряда).
Умножение матриц. Даны матрица  , имеющая , имеющая  строк и строк и  столбцов, и матрица столбцов, и матрица  , имеющая , имеющая  строк и строк и  столбцов. Произведением этих матриц называется матрица, обозначаемая столбцов. Произведением этих матриц называется матрица, обозначаемая  ( ( – первая матрица), элементы – первая матрица), элементы  которой определяются формулой которой определяются формулой
 , ,  , ,  . (6) . (6)
Изобразим схематично эти матрицы и их произведение:
 . .
В формуле (6) первые индексы означают номера строки элемента матрицы, вторые – номера столбца элемента. Формула (6) показывает, что элемент  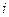 -й строки и -й строки и  -го столбца матрицы -го столбца матрицы  равен сумме произведений элементов равен сумме произведений элементов 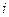 -й строки первой матрицы -й строки первой матрицы  на соответствующие элементы на соответствующие элементы  -го столбца второй матрицы -го столбца второй матрицы  . Следовательно, чтобы получить элементы . Следовательно, чтобы получить элементы  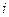 -й строки матрицы -й строки матрицы  , нужно элементы , нужно элементы 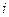 -й строки -й строки  умножить на соответствующие элементы первого столбца умножить на соответствующие элементы первого столбца  , и, сложив, найти , и, сложив, найти 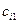 . Умножив элементы . Умножив элементы 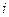 -й строки -й строки  на соответствующие элементы второго столбца на соответствующие элементы второго столбца  и сложив, получим и сложив, получим  и т. д. Умножив элементы и т. д. Умножив элементы 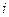 -й строки -й строки  на соответствующие элементы на соответствующие элементы  -го столбца -го столбца  и сложив, получим и сложив, получим  . .
Таким образом, элементы  -й строки матрицы С получаются с помощью -й строки матрицы С получаются с помощью 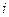 -й строки первой матрицы -й строки первой матрицы  . Это относится к любой строке матрицы С. Поэтому ясно, что число строк С равно числу строк . Это относится к любой строке матрицы С. Поэтому ясно, что число строк С равно числу строк  , а число столбцов , а число столбцов  равно числу столбцов матрицы В, так как номер столбца равно числу столбцов матрицы В, так как номер столбца  элемента элемента  совпадает с номером столбца совпадает с номером столбца  матрицы матрицы  . .
Аналогично найдём  , если число столбцов матрицы , если число столбцов матрицы  равно числу строк матрицы равно числу строк матрицы  . Если это не так, то произведения . Если это не так, то произведения  не существует. Если даже не существует. Если даже  и и  существуют, то легко проверить на примерах, что, вообще говоря, существуют, то легко проверить на примерах, что, вообще говоря,  . .
Свойства умножения матриц. Пусть даны три матрицы  , ,  и и  . Тогда: . Тогда:
·  ; ;
·  . .
Пусть  – квадратная матрица, а – квадратная матрица, а  – единичная матрица того же порядка, что и – единичная матрица того же порядка, что и  . Нетрудно проверить, что . Нетрудно проверить, что  . .
Обратная матрица. Пусть дана квадратная матрица
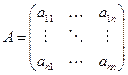
Определитель этой матрицы есть число
 . .
Пусть этот определитель не равен нулю и  – алгебраическое дополнение для элемента – алгебраическое дополнение для элемента  . .
Обратной к данной матрице  называется матрица, обозначаемая называется матрица, обозначаемая  и определяемая условиями и определяемая условиями  Если Если  то то 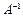 есть матрица вида есть матрица вида
 . .
Отсюда видно, что для построения обратной матрицы  для матрицы для матрицы  нужно: нужно:
· элементы матрицы  заменить на их алгебраические дополнения; заменить на их алгебраические дополнения;
· все эти дополнения поделить на  – определитель матрицы – определитель матрицы  ; ;
· полученную матрицу транспонировать.
Из приведенного определения видно, что для нахождения  нужно вычислить определитель матрицы нужно вычислить определитель матрицы  и все алгебраические дополнения для всех ее элементов. и все алгебраические дополнения для всех ее элементов.
§4. Системы  линейных алгебраических уравнений линейных алгебраических уравнений
с  неизвестными. Матричный метод решения неизвестными. Матричный метод решения
Дана система уравнений
 , (7) , (7)
где 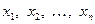 – искомые неизвестные, – искомые неизвестные,  – заданные числа, называемые коэффициентами уравнений системы, – заданные числа, называемые коэффициентами уравнений системы,  – заданные числа, называемые свободными членами системы уравнений. Нужно найти – заданные числа, называемые свободными членами системы уравнений. Нужно найти 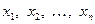 . .
Введём три матрицы
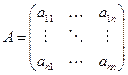 , (8) , (8)
 , (9) , (9)
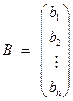 . (10) . (10)
 называется матрицей коэффициентов системы (7), называется матрицей коэффициентов системы (7),  – матрицей неизвестных, – матрицей неизвестных,  – матрицей свободных членов. Определитель матрицы – матрицей свободных членов. Определитель матрицы  называется определителем системы и обозначается называется определителем системы и обозначается  . Итак, определитель системы (7) равен . Итак, определитель системы (7) равен
 . (11) . (11)
Возьмём произведение  матриц (8) и (9). Так как матриц (8) и (9). Так как  – столбцевая матрица, то это произведение также представляет собой столбцевую матрицу – столбцевая матрица, то это произведение также представляет собой столбцевую матрицу
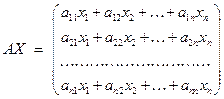 . .
Элементы этого произведения равны согласно системе (7) свободным членам соответствующих уравнений этой системы, т. е. соответствующим элементам матрицы  . Следовательно, эти две матрицы равны друг другу. Таким образом, . Следовательно, эти две матрицы равны друг другу. Таким образом,
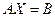 . (12) . (12)
Это есть матричная запись системы (7).
Пусть определитель системы (7), т. е. определитель (11), отличен от нуля. Тогда по известной матрице (8) коэффициентов системы (7) найдём для неё обратную матрицу  . На эту матрицу (все элементы которой известны) умножим обе части (12), считая матрицу . На эту матрицу (все элементы которой известны) умножим обе части (12), считая матрицу  первой матрицей в произведениях, и получим первой матрицей в произведениях, и получим
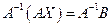 . (13) . (13)
Согласно первому свойству умножения матриц, левая часть формулы (13) равна  , но так как , но так как 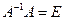 , ,  , то левая часть формулы (13) равна , то левая часть формулы (13) равна  . Таким образом, . Таким образом,
 . (14) . (14)
Правая часть формулы содержит известные матрицы. Найдём произведение  . Это будет столбцевая матрица с известными элементами, но эта матрица по формуле (14) равна матрице неизвестных . Это будет столбцевая матрица с известными элементами, но эта матрица по формуле (14) равна матрице неизвестных  . Поэтому их соответствующие элементы равны друг другу. Приравняв эти элементы, найдём неизвестные . Поэтому их соответствующие элементы равны друг другу. Приравняв эти элементы, найдём неизвестные 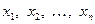 . .
Формулы Крамера
Покажем, что решение системы (7) определяется формулами Крамера
 (15) (15)
Здесь  – определитель системы (7) (считается, что – определитель системы (7) (считается, что  ). ).  – определители, получаемые из определителя D заменой соответственно первого, второго, … – определители, получаемые из определителя D заменой соответственно первого, второго, …  -го его столбца на столбец свободных членов системы (7), т. е. -го его столбца на столбец свободных членов системы (7), т. е.
 , ,  , ,
…….
 . .
Запишем разложение определителя (11) системы (7) по элементам первого столбца:
 (16) (16)
В этой формуле элементы первого столбца  заменим соответственно на заменим соответственно на  – свободные члены системы (7). Тогда – свободные члены системы (7). Тогда
 . (17) . (17)
Получили разложение определителя  по элементам первого столбца. Аналогично запишем разложение определителя по элементам первого столбца. Аналогично запишем разложение определителя  по элементам второго столбца по элементам второго столбца
 (18) (18)
и т. д. Наконец, получим разложение определителя  по элементам последнего столбца: по элементам последнего столбца:
 . (19) . (19)
По формуле (14) будем иметь
 . .
В правой части матрицы перемножим и получим столбцевую матрицу. Теперь последнюю формулу запишем так:
 . .
Согласно (17) – (19) в последней формуле суммы, стоящие в числителях матрицы правой части, равны соответственно  . Следовательно, эту формулу можно записать в виде . Следовательно, эту формулу можно записать в виде
 . .
В этом соотношении матрицы слева и справа равны друг другу, следовательно, их соответствующие элементы равны, т. е. получаем соотношение (15). Из формул Крамера вытекает следующая
Теорема. Если определитель системы (7) не равен нулю, то эта система имеет единственное решение (которое можно найти, например, по формулам Крамера).
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




