Симплекс-метод решения задачи линейного программирования
Задание 3. Решить симплексным методом задачу линейного программирования (ЗЛП).
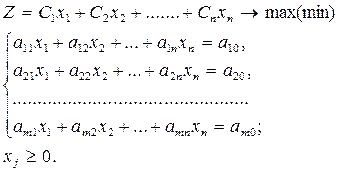
1. Прежде чем решать задачу симплексным методом, надо
проверить, что правые части системы ограничений неотрицательны, т.е.  . Если это не так, то в соответствующем ограничении меняем знак. . Если это не так, то в соответствующем ограничении меняем знак.
2. Далее исходную задачу надо записать в канонической форме,
если она не имеет такой формы записи. Для этого каждое ограничение - неравенство вида « » надо превратить в равенство добавлением дополнительной неотрицательной (балансовой) переменной, а каждое ограничение - неравенство вида « » надо превратить в равенство добавлением дополнительной неотрицательной (балансовой) переменной, а каждое ограничение - неравенство вида «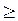 » превратить в равенство вычитанием балансовой переменной. Таким образом, все ограничения в задаче будут уравнения с неотрицательными правыми частями. » превратить в равенство вычитанием балансовой переменной. Таким образом, все ограничения в задаче будут уравнения с неотрицательными правыми частями.
3. Далее систему уравнений при помощи симплексных
преобразований надо привести к единичному базису, т.е. найти исходное опорное решение  . .
4. Для того чтобы проверить, будет ли это решение
оптимальным, надо составить оценочную строку (Z-строку) по следующему правилу:  , ,
где  - искомый элемент Z-строки; - искомый элемент Z-строки;
 - столбец коэффициентов целевой функции при базисных переменных; - столбец коэффициентов целевой функции при базисных переменных;
 - столбец коэффициентов при неизвестном - столбец коэффициентов при неизвестном  ; ;
 - столбец свободных членов; - столбец свободных членов;
 - скалярное произведение указанных столбцов – векторов; - скалярное произведение указанных столбцов – векторов;
 - коэффициент целевой функции при неизвестном - коэффициент целевой функции при неизвестном  . .
5. Для задачи на максимум.
Если в Z-строке все элементы положительные,  , то найдено , то найдено
оптимальное решение  . Если же в Z-строке есть хотя бы один отрицательный элемент, то найденное решение не оптимально. Есть возможность его улучшения. Для этого среди отрицательных элементов Z-строки находим минимальный (например . Если же в Z-строке есть хотя бы один отрицательный элемент, то найденное решение не оптимально. Есть возможность его улучшения. Для этого среди отрицательных элементов Z-строки находим минимальный (например  ). Столбец с номером p становится разрешающим. Разрешающую строку выбираем по симплексным преобразованиям (для этого в симплексной таблице заводится последний столбец). В столбце с номером p в качестве разрешающего элемента берется положительный элемент, если он один. Если в этом столбце положительных элементов несколько, то берется тот из них, для которого отношение свободных членов к этим положительным элементам будет наименьшее. Если в столбце с номером p вообще нет положительных элементов, то задача не имеет оптимального решения и ). Столбец с номером p становится разрешающим. Разрешающую строку выбираем по симплексным преобразованиям (для этого в симплексной таблице заводится последний столбец). В столбце с номером p в качестве разрешающего элемента берется положительный элемент, если он один. Если в этом столбце положительных элементов несколько, то берется тот из них, для которого отношение свободных членов к этим положительным элементам будет наименьшее. Если в столбце с номером p вообще нет положительных элементов, то задача не имеет оптимального решения и  . После того как разрешающий элемент найден, производим расчеты по методу Гаусса, включая и элементы Z-строки. Получаем новое опорное решение. После этого возвращаемся к началу пункта 5. . После того как разрешающий элемент найден, производим расчеты по методу Гаусса, включая и элементы Z-строки. Получаем новое опорное решение. После этого возвращаемся к началу пункта 5.
6. Для задачи на минимум. Если в Z-строке все элементы  , ,
то найдено оптимальное решение  . Если же в Z- строке есть хотя бы один положительный элемент, то найденное решение не оптимально. Для улучшения решения среди положительных элементов Z-строки находим максимальный (например . Если же в Z- строке есть хотя бы один положительный элемент, то найденное решение не оптимально. Для улучшения решения среди положительных элементов Z-строки находим максимальный (например  ). Столбец с номером q становится разрешающим. Разрешающую строку ищем по симплексным преобразованиям (смотреть задачу на максимум). Если в столбце с номером q нет положительных элементов, то задача не имеет оптимального решения и ). Столбец с номером q становится разрешающим. Разрешающую строку ищем по симплексным преобразованиям (смотреть задачу на максимум). Если в столбце с номером q нет положительных элементов, то задача не имеет оптимального решения и  . После того, как разрешающий элемент выбран, выполняем расчеты по методу Гаусса, включая и элементы Z-строки, и получаем новое опорное решение. Переходим к началу пункта 6. Процесс продолжается до тех пор, пока не будет найдено оптимальное решение или мы не убедимся, что его нет. . После того, как разрешающий элемент выбран, выполняем расчеты по методу Гаусса, включая и элементы Z-строки, и получаем новое опорное решение. Переходим к началу пункта 6. Процесс продолжается до тех пор, пока не будет найдено оптимальное решение или мы не убедимся, что его нет.
Пример. Решить задачу линейного программирования симплексным методом
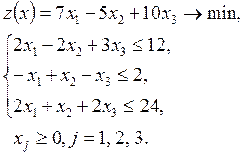
Решение. Приведем задачу к каноническому виду. Для этого в левую часть каждого неравенства типа « » добавляем новые дополнительные переменные » добавляем новые дополнительные переменные  , ,  , ,  (новые балансовые переменные). Таким образом, задача примет вид (новые балансовые переменные). Таким образом, задача примет вид
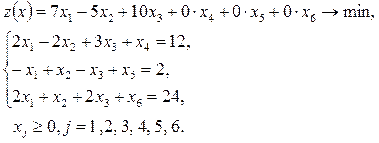
Составляем симплекс-таблицу.

| базис
|
|
| -5
|
|
|
|
| 
| 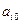
| 
| 
| 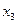
| 
| 
| 
| |
| 
|
|
| -2
|
|
|
|
| –
| |
| 
|
| -1
|  1 1
| -1
|
|
|
| 2:1=2 – min
| |
| 
|
|
|
|
|
|
|
| 24:1=24
| |
| 
|
| -7
| 5
| -10
|
|
|
|
| |
| 
|
|
|
|
|
|
|
|
| |
| 
|
| -1
|
| -1
|
|
|
|
| |
| 
|
|
|
|
|
| -1
|
|
| |
| 
| -10
| -2
|
| -5
|
| -5
|
|
|
Так как есть исходное опорное решение, то составляем оценочную
Z-строку по следующему правилу:  . .
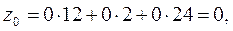
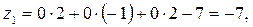
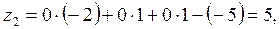
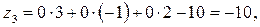
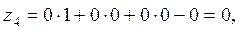
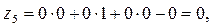
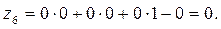
Так как среди  есть одно положительное число, то столбик, в котором содержится этот элемент, выбираем в качестве разрешающего. Разрешающий элемент выбираем по методу минимального элемента ( есть одно положительное число, то столбик, в котором содержится этот элемент, выбираем в качестве разрешающего. Разрешающий элемент выбираем по методу минимального элемента ( ). Далее вычисления производим по методу Жордана–Гаусса. ). Далее вычисления производим по методу Жордана–Гаусса.
Находим, что все  , значит найденное решение оптимально, при этом , значит найденное решение оптимально, при этом  , ,  . Исходная задача имела три переменных, поэтому в ответе в оптимальном решении последние три дополнительные переменные не записываем. . Исходная задача имела три переменных, поэтому в ответе в оптимальном решении последние три дополнительные переменные не записываем.
Ответ:  , ,  . .
Транспортная задача
Задание 4. Решить транспортную задачу.
Транспортная задача - это задача о перевозке некоторого груза от m поставщиков к n потребителям. Обычно условия транспортной задачи задаются в таблице.
| А\В
|  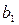
| 
| 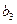
| ……
| 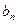
| 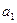
| 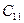
| 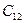
| 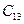
| ……..
| 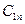
| 
| 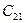
| 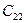
| 
| …….
| 
| | ……
| …….
| …….
| …….
| …….
| …….
| 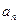
| 
| 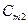
| 
| …….
| 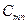
| В этой таблице:
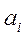 - запас груза у поставщика - запас груза у поставщика 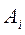 , где i=1, 2,…, m; , где i=1, 2,…, m;
 - потребность в грузе у потребителя - потребность в грузе у потребителя 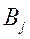 , где j=1, 2,…, n; , где j=1, 2,…, n;
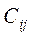 - стоимость перевозки единицы груза от i- гопоставщика к j -му - стоимость перевозки единицы груза от i- гопоставщика к j -му
потребителю (тариф перевозки).
Если суммарный запас равен суммарным потребностям, т.е. 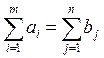 , то имеем закрытую модель транспортной задачи. Если нет, то открытую модель. , то имеем закрытую модель транспортной задачи. Если нет, то открытую модель.
Рассмотрим решение закрытой модели транспортной задачи.
1. Как и при решении ЗЛП симплексным методом, определение оптимального плана транспортной задачи начинают с нахождения исходного опорного плана. Этот план наиболее рационально находить методом минимального элемента (существуют и другие методы его нахождения). Для этого в таблице тарифов выбираем минимальный (например  ) и в клетку, которая ему соответствует, помещаем наименьшее из чисел ) и в клетку, которая ему соответствует, помещаем наименьшее из чисел 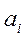 и и 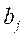 . Затем из рассмотрения исключаем либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены. Так на каждом шаге исключается либо один поставщик, либо один потребитель. При этом если клетка подлежит заполнению, но запасы равны нулю, то на этом шаге в соответствующую клетку заносится базисный нуль (0*). Из оставшейся части таблицы снова выбираем минимальный тариф и т.д. до тех пор, пока все запасы не будут распределены, а потребители удовлетворены. Если минимальных элементов несколько, то выбираем ту клетку, которой соответствует наибольшая перевозка. Таким образом, находим исходный опорный план. Этот опорный план должен содержать . Затем из рассмотрения исключаем либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены. Так на каждом шаге исключается либо один поставщик, либо один потребитель. При этом если клетка подлежит заполнению, но запасы равны нулю, то на этом шаге в соответствующую клетку заносится базисный нуль (0*). Из оставшейся части таблицы снова выбираем минимальный тариф и т.д. до тех пор, пока все запасы не будут распределены, а потребители удовлетворены. Если минимальных элементов несколько, то выбираем ту клетку, которой соответствует наибольшая перевозка. Таким образом, находим исходный опорный план. Этот опорный план должен содержать 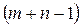 занятую клетку. занятую клетку.
2. Для проверки найденного плана на оптимальность используется метод потенциалов.
2.1 Для «заняты х» клеток составляем систему уравнений
 , где , где  - потенциалы поставщиков, - потенциалы поставщиков,  - потенциалы потребителей. Получаем - потенциалы потребителей. Получаем  линейных уравнений с линейных уравнений с 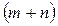 неизвестными. Такая система имеет множество решений. Чтобы найти любое из них, надо одной из переменных дать произвольное значение (например неизвестными. Такая система имеет множество решений. Чтобы найти любое из них, надо одной из переменных дать произвольное значение (например 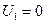 ). Находим значения остальных потенциалов. ). Находим значения остальных потенциалов.
2.2 Для «свободных» клеток находим числа  . .
Если все 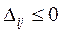 , то найденный опорный план будет оптимальным. Если есть хотя бы один , то найденный опорный план будет оптимальным. Если есть хотя бы один 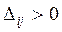 , то найденное решение не оптимально. Среди всех положительных , то найденное решение не оптимально. Среди всех положительных  находим одно максимальное (например находим одно максимальное (например  ) и делаем перераспределение поставок груза относительно свободной клетки ) и делаем перераспределение поставок груза относительно свободной клетки 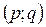 . Если среди всех положительных . Если среди всех положительных  имеется несколько одинаковых максимальных, то выбираем любое. имеется несколько одинаковых максимальных, то выбираем любое.
Перераспределение поставок в таблице условий транспортной задачи производится по циклу.
Цикл – это цепь, многоугольник, все вершины которого находятся в занятых клетках, углы прямые, число вершин четное. После того как цикл пересчета построен, в вершинах цикла, начиная со свободной клетки  , ставим поочередно «+» и «–». Далее в «–» клетках находим минимальный груз , ставим поочередно «+» и «–». Далее в «–» клетках находим минимальный груз 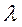 , который прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Таким образом, свободная клетка , который прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Таким образом, свободная клетка 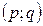 становится занятой с грузом, а одна занятая клетка освобождается. Общее число занятых клеток в новом опорном плане должно сохраняться, т.е. становится занятой с грузом, а одна занятая клетка освобождается. Общее число занятых клеток в новом опорном плане должно сохраняться, т.е. 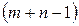 . .
Этот новый план распределения поставок проверяем на оптимальность (переходим к пункту 2). Процесс продолжаем до тех пор, пока не получим, что все 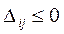 . После того как оптимальный план перевозок будет найден, выписываем опорный план и находим минимальную стоимость перевозок. . После того как оптимальный план перевозок будет найден, выписываем опорный план и находим минимальную стоимость перевозок.
Пример. Имеются четыре пункта поставки однородного груза  , , 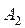 , , 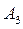 , ,  , в каждом из которых находится груз соответственно в количестве , в каждом из которых находится груз соответственно в количестве 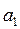 , , 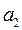 , ,  , ,  тонн и пять пунктов потребления этого груза тонн и пять пунктов потребления этого груза 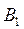 , ,  , , 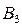 , ,  , ,  . В пункты . В пункты 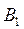 , ,  , , 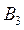 , , 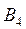 , , 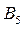 требуется доставить соответственно требуется доставить соответственно  , , 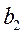 , ,  , , 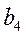 , ,  тонн груза. Транспортные расходы при перевозке единицы груза из пункта тонн груза. Транспортные расходы при перевозке единицы груза из пункта 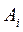 в пункт в пункт 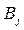 равны равны 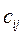 , где i= 1, 2, 3, 4, j= 1, 2, 3, 4, 5. Найти такой план закрепления потребителей за поставщиками, чтобы затраты по перевозкам были минимальными, при условии: , где i= 1, 2, 3, 4, j= 1, 2, 3, 4, 5. Найти такой план закрепления потребителей за поставщиками, чтобы затраты по перевозкам были минимальными, при условии:  – пункты поставки груза, – пункты поставки груза,
 – пункты потребления, – пункты потребления,
 – тарифы. – тарифы.
Решение. По условию задачи составим таблицу:
1. Найдем суммарный запас и суммарные потребности:
 , ,  . .
Так как суммарный запас равен суммарным потребностям, т.е.  , то имеем закрытую модель транспортной задачи. , то имеем закрытую модель транспортной задачи.
2. Находим исходный опорный план методом минимального элемента. Число занятых клеток должно равняться:  . .
 

| 
| 
| 
| 
| 
|
| 
|   6 6
|
|  20 20
|  17 17
|
|  12 12
| 
|    1 1
|  25 25
|    3 3
|  18 18
|   17 17
|
| 
|     9 9
|
|
 5 5
|
|
|  18 18
|  
|
|   15 15
|
|  3 3
|  28 28
|
| 
|
|
|  12 12
|
|
|
| Среди всех тарифов перевозки  находим наименьший. В нашей задаче находим наименьший. В нашей задаче  , в клетку , в клетку  пишем наименьшее из чисел: запас поставщика пишем наименьшее из чисел: запас поставщика  или потребности потребителя или потребности потребителя  , т.е. , т.е.  . Так как потребность первого потребителя . Так как потребность первого потребителя  полностью удовлетворили, то его исключаем из дальнейшего рассмотрения, а запас у поставщика полностью удовлетворили, то его исключаем из дальнейшего рассмотрения, а запас у поставщика 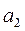 остался равным остался равным  . Далее из оставшейся части таблицы снова выбираем наименьший тариф перевозки, и т.д. до тех пор, пока все запасы не будут распределены, потребители удовлетворены. . Далее из оставшейся части таблицы снова выбираем наименьший тариф перевозки, и т.д. до тех пор, пока все запасы не будут распределены, потребители удовлетворены.
3. Проверяем найденный план на оптимальность методом потенциалов:
3.1 Для «занятых» клеток составляем уравнения  : :
 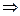 
3.2 Для «свободных» клеток находим  : :

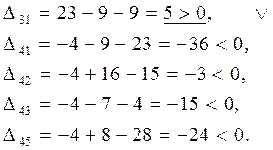
Строим в таблице цикл пересчета относительно клетки (3, 1). Он пойдет следующим образом (3, 1)  (2, 1) (2, 1)  (2, 3) (2, 3)  (3, 3). (3, 3).
Расставляем знаки «+» и «–» в вершинах цикла, начиная с клетки (3, 1). В «–» клетках ищем минимальный груз  .Этот груз .Этот груз  прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок: прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок:
4. Проверяем найденный план на оптимальность методом потенциалов.
4.1 Для «занятых» клеток:
 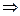 
4.2 Для «свободных» клеток:
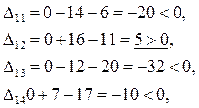
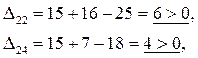
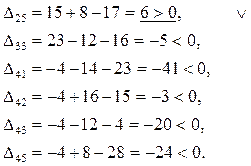
Строим в таблице цикл пересчета относительно клетки (2, 5). Он пойдет следующим образом (2, 5)  (2, 1) (2, 1)  (3, 1) (3, 1)  (3, 5). (3, 5).
Расставляем знаки «+» и «–» в вершинах цикла, начиная с клетки (2, 5). В «–» клетках ищем минимальный груз  .Этот груз .Этот груз  прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок: прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок:
5. Проверяем найденный план на оптимальность.
5.1 Для «занятых» клеток:
 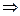 
5.2 Для «свободных» клеток:
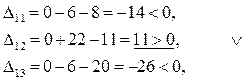

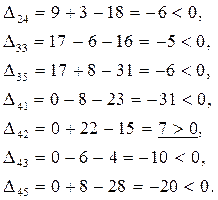
Строим в таблице цикл пересчета относительно клетки (1, 2). Он пойдет следующим образом (1, 2)  (1, 5) (1, 5)  (2, 5) (2, 5)  (2, 1) (2, 1)  (3, 1) (3, 1)  (3, 2). (3, 2).
Расставляем знаки «+» и «–» в вершинах цикла, начиная с клетки (1, 2). В «–» клетках ищем минимальный груз  . Этот груз . Этот груз  прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок: прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок:
6. Проверяем найденный план на оптимальность.
6.1 Для «занятых» клеток:
 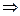 
6.2 Для «свободных» клеток:
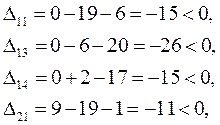
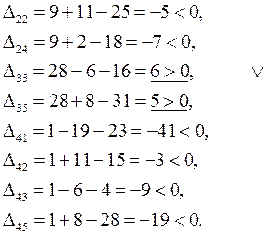
Строим в таблице цикл пересчета относительно клетки (3, 3). Он пойдет следующим образом (3, 3)  (2, 3) (2, 3)  (2, 5) (2, 5)  (1, 5) (1, 5)  (1, 2) (1, 2)  (3, 2). (3, 2).
Расставляем знаки «+» и «–» в вершинах цикла, начиная с клетки (3, 3). В «–» клетках ищем минимальный груз  .Этот груз .Этот груз  прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок: прибавляем к грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый план перевозок:
7. Проверяем найденный план на оптимальность.
7.1 Для «занятых» клеток:
 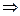 
7.2 Для «свободных» клеток:
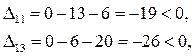

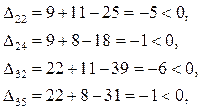
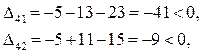

Так как все  , найденный план является оптимальным. , найденный план является оптимальным.

8. Найдем минимальную стоимость перевозок:

Ответ: 
Задания к контрольной работе
Вариант 1
Задание 1
Вероятности землетрясения в каждом из трех городов соответственно равны 0,1; 0,8 и 0,6. Найти вероятность того, что землетрясение произойдет хотя бы в одном городе.
Задание 2
В корзине три сорта яблок: 20 – первого, 15 – второго и 25 – третьего. Вероятность высокого содержания сахара в каждом из них соответственно равна 0,5, 0,6, 0,7. Наудачу взятое яблоко оказалось с высоким содержанием сахара. Найти, что это яблоко 1 сорта.
Задание 3
Дано статистическое распределение выборки: в первой строке указаны выборочные варианты  , а во второй строке – соответственные частоты , а во второй строке – соответственные частоты  количественного признака количественного признака  . Требуется найти: . Требуется найти:
1) выборочную среднюю;
2) выборочное среднее квадратическое отклонение;
3) моду и медиану.
Задание 4
Решить методом Жордана–Гаусса систему линейных уравнений:
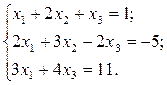
Задание 5
Решить графически задачу линейного программирования:
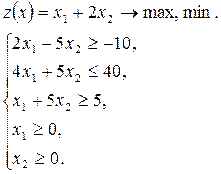
Задание 6
Решить симплексным методом следующую задачу линейного программирования:
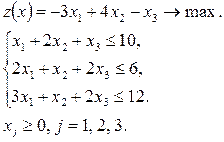
Задание 7
Решить транспортную задачу. Имеются четыре пункта поставки однородного груза  , , 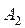 , , 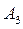 , ,  , в каждом из которых находится груз соответственно в количестве , в каждом из которых находится груз соответственно в количестве 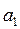 , , 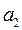 , ,  , ,  тонн и пять пунктов потребления этого груза тонн и пять пунктов потребления этого груза 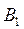 , ,  , , 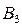 , ,  , ,  . В пункты . В пункты 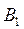 , ,  , , 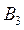 , , 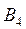 , , 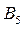 требуется доставить соответственно требуется доставить соответственно  , , 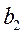 , ,  , , 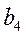 , ,  тонн груза. Транспортные расходы при перевозке единицы груза из пункта тонн груза. Транспортные расходы при перевозке единицы груза из пункта 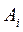 в пункт в пункт 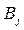 равны равны 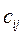 , где i= 1, 2, 3, 4, j= 1, 2, 3, 4, 5. Найти такой план закрепления потребителей за поставщиками, чтобы затраты по перевозкам были минимальными, учитывая: , где i= 1, 2, 3, 4, j= 1, 2, 3, 4, 5. Найти такой план закрепления потребителей за поставщиками, чтобы затраты по перевозкам были минимальными, учитывая:  , ,
 , ,
 . .
Вариант 2
Задание 1
Вероятности выполнить норму для каждого из трех спортсменов соответственно равны 0,7; 0,8 и 0,9. Найти вероятность того, что ее выполнит только один из них.
Задание 2
В библиотеке 90 учебников по математике разных лет издания: 25 – 1972 г., 35 – 1983 г. и 30 – 1995 г. Вероятности того, что учебники удовлетворяют программе, соответственно равны 0,6, 0,7, 0,8. Наудачу взятый учебник соответствует про
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




