Пределение усилий в стержнях фермы

Из довольно большого числа способов определения уси­лий в стержнях ферм чаще всего применяются на практике три способа:

1. Способ вырезания узлов;

2. Метод Риттера – метод сечений;

3. Графический метод - построение диаграммы Максвелла-Кремоны.

Способ вырезания узлов заключается в том, что для опре­деления усилий во всех стержнях фермы необходимо вырезать последовательно узлы фермы и, рассматривая равновесие уз­лов, определить усилия в стержнях, сходящихся в рассматри­ваемом узле. При этом нужно начинать вырезать узел, в кото­ром сходятся только два стержня, а далее последовательно вырезаются узлы, в которых сходятся не более двух стержней с неизвестными усилиями.

Метод Риттера заключается в том, что ферма мысленно рассекается на две части. Рассматривая условия равновесия какой-либо отсеченной части и составляя соответствующие уравнения, мы можем оп­ределить неизвестные усилия во всех перерезанных стержнях, если их число равно трем (по числу уравнений равновесия, ко­торые можно составить для плоской системы сил). Эти урав­нения желательно составить таким образом, чтобы в каждое из них входило только одно неизвестное усилие в стержне. Та­ким уравнением оказывается в различных случаях либо урав­нение моментов относительно определенной точки (способ «моментной точки»), либо уравнение проекции на какую-либо ось («способ проекций»).

Способ проекций, как правило, применяется при расчете ферм с параллельными поясами.

Способ моментной точки применяется главным образом в тех случаях, когда удается рассечь ферму на две части так, чтобы при этом перерезанными оказались три ее стержня, на­правления осей которых не пересекаются в одной точке.

Для определения усилия в каком-либо стержне необходи­мо разрезать ферму так, чтобы в разрез, кроме данного стер­жня, попали еще два других (оси которых не сходятся с ним в общей точке), после чего из уравнения моментов относитель­но точки пересечения осей этих двух стержней можно легко определить усилия в данном стержне.

Точка пересечения осей двух стержней, относительно которой составляется уравнений моментов, называется момент­ной..

В начале расчета фермы иногда удается сразу отметить стержни, усилия в которых при данной нагрузке равны нулю. Такие стержни называются нулевыми.

Признаков нулевых стержней два:

1). Если в узле сходятся два стержня, не лежащих на одной прямой (рис. 5.6.), и внешних сил к узлу не приложено, то усилия в обоих стержнях будут равны нулю.

Рис. 5.6. Первый признак нулевого стержня

2). Если в узле сходятся три стержня, два из которых лежат на одной прямой, а третий примыкает к ним под некоторым углом (рис. 5.7.), а внешних сил к узлу не приложено, то усилие в примы­кающем третьем стержне равно нулю.

Рис. 5.7. Второй признак нулевого стержня

Частный случай второго признака:

Если в узле сходятся три стержня, два из которых лежат на одной прямой, а третий примыкает к ним под некоторым углом, и по направлению третьего стержня к узлу приложена сила (рис. 5.8.), то усилие в примыкающем третьем стержне равно при­ложенной к узлу силе.

Рис. 5.8. Частный случай второго признака

Графический метод определения усилий в стержнях фермы – построение диаграммы Максвелла-Кремоны.

Сущность графического метода определения усилий в стер­жнях фермы состоит в построении силового многоугольника для каждого из узлов ферм.

При этом силовых многоугольников будет столько, сколько узлов в ферме. Этот метод довольно трудоемок, т.к. требует большое количество графических построений. Целесообразно строить все многоугольники сил не отдельно для каждого узла, а вместе, что позволяет диаграмма Максвелла-Кремоны.

Порядок определения усилий в ферме графическим способом с помощью построения диаграммы Максвелла-Кремоны:

1. Вычерчиваем ферму в строгом соответствии с масштабом длин.

2. Определяем величину и направление опорных реакций ана­литическим или графическим способом.

3. Нумеруем поля расчетной схемы: - внешние поля - заглав­ными буквами латинского алфавита; внутренние поля - араб­скими цифрами.

4. Строим в масштабе сил многоугольник внешних сил, дей­ствующих на ферму, обходя ферму по часовой стрелке. Сипы обозначаем соответствующими полями, примыкающими к данной силе.

5. Строим диаграмму усилий для стержней фермы, для чего:

а) обходим по часовой стрелке узел, в котором сходится два стержня и строим силовой многоугольник для этого узла. Усилия в стержнях нумеруем соответствующими полями. Построение следует начинать с известных сил и наносить все силы в том порядке, в каком они встречаются при обхо­де данного узла по ходу части стрелки.

б) переходим к следующему узлу, в котором сходится не более 2-х стержней с неизвестными усилиями и повторяем предыдущее построение, и т.д.

6. Контролем правильности построения является параллельность последнего стержня на ферме последнему соответ­ствующему отрезку на диаграмме.

7. Определяем усилие в стержнях фермы. Для этого измеря­ем отрезки, соответствующие стержням фермы на диаграм­ме и в соответствии с масштабом сил вычисляем величину усилия.

8. Определяем знаки усилий в стержнях фермы. При опреде­лении знака усилия читаем наименование стержня, обходя узел по часовой стрелке (1-2).

В такой же последовательности (допустим 1-2) читаем наи­менование усилия на диаграмме усилий. Направление чтения определит направление действующего

усилия: к узлу (–), от узла (+).

9. Все полученные данные о величине и знаке усилия в стерж­нях сводятся в таблицу.

10. Производим сравнение результатов аналитического и гра­фического расчетов и вычисляем погрешность производи­мых расчетов.

Пример расчета 5.1.

Определить усилия в отмеченных стержнях фермы аналитическим и

графическим способом.

Для определения усилий необходимо вычертить схему фермы с указанием конкретных геометричес­ких размеров и нагрузок.

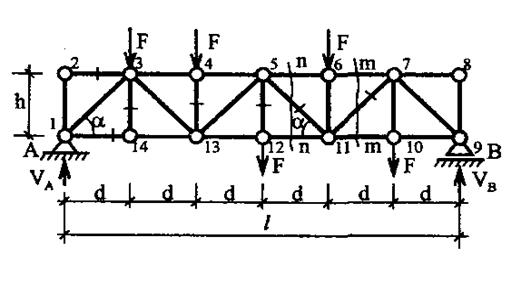
Рис. 5.9.Расчетная схема фермы

Аналитический расчет фермы

1. Определение опорных реакций

На рис. 5.9. представлена ферма, условия опирания которой такие же, как у простой балки. Такая ферма называется ба­лочной. Как и у простых балок, в балочных фермах при дей­ствии вертикальных нагрузок возникают только вертикальные опорные реакции. Их определение производится так же, как и в простых балках.

Вертикальные опорные реакции можно определить, пользу­ясь только 2-мяуравнениями статики:

1) Σ М_А = 0; 2) Σ М_В= 0,

где Σ М_А - сумма моментов всех сил относительно точки А;

Σ М_В - сумма моментов всех сил относительно точки В.

Раскрыв значение Σ М_А и Σ М_В, получим:

Vв·l - F· 5d - F· 4d - F· 3d - F· 2d - F· d = 0

V_A·l - F· 5d - F· 4d - F· 3d - F· 2d - F· d = 0

Из первого уравнения определим величину опорной реакции V_В:

Vв = 25 кН

Из второго уравнения определим величину вертикальной реакции V_A:

V_A = 25 кН.

После вычисления опорных реакций следует убедиться в правильности их определений, т.к. ошибка в определении их приведет к ошибкам и в определении внутренних усилий в стер­жнях фермы.

Для проверки правильности полученных результатов реко­мендуется составить третье уравнение равновесия, которое не использовалось при определении опорных реакций.

Если вертикальные опорные реакции определены верно, то сумма проекций всех сил на вертикальную ось должна быть тождественно равна нулю, т.е.

ΣFу = 0;

V_A + V_B-5F =25 +25 -5·10 = 0.

Результаты проверки свидетельствуют о том, что верти­кальные опорные реакции определены верно.

2. Определение усилий в стержнях фермы методом вырезания узлов.

В рассматриваемом примере (рис. 5.9.) нулевыми стержня­ми фермы являются стержни 2-3 (из рассмотрения узла 2) и 8-7 (из рассмотрения узла 8) по первому признаку нулевых стержней.

Стержень 3-14 также нулевой по второму признаку нуле­вых стержней (из рассмотрения узла 14 рис. 5.10.).

Рис. 5.10. Равновесие узла 14

Пользуясь частным случаем второго признака нулевых стержней, можно определить без вычисления усилия в стер­жнях 4—13, 5—12. Усилия в стержне 4-13 равно— F, т.е. N_4-13= —F; знак (—) указывает на то, что стержень сжат. И действи­тельно, рассматривая узел 4, мы можем убедиться в том (рис. 5.11.).

Рис. 5.11. Равновесие узла 4

Вырезав узел, показываем направление усилий от узла, т.е. предполагаем, что все стержни растянуты.

Выбираем оси ко­ординат таким образом, чтобы одна из осей (ось х)совпала с направлением усилий N_4-13 и N_4-13

Составляем уравнение равновесия всех сил, сходящихся в одной точке.

Это уравнение должно включить в себя только одно неизвестное усилие N_4-13. Для этого спроектируем все силы на вертикальную ось у:

-F- N_4-13 =0; N_4-13 = - F = -10 кН.

Рассуждая таким же образом, определяем усилие в стер­жне 5—12.

N_5-12 = F.

Усилие в стержне 1-14 определяем способом вырезания узла. Вырезаем узел 1 и рассматриваем его равновесие. В данном узле сходятся 3 стержня, но неизвестных усилий только два (N_1-3 и N_1-14). Усилие N_1-2 = 0 (по первому признаку нуле­вых стержней, рассматривая узел 2).

Выбираем оси координат так, чтобы одна из осей (ось х) совпала с направлением «ненужного» нам усилия (N_1-3).

Проектируем все силы на ось У и составляем уравнение:

Рис. 5.12. Равновесие узла 1

ΣFу = 0;

V_A·cosα - N_1-14·sinα = 0 N_1-14 = V_A·cosα / sinα = V_A ·ctgα

сtgα = 4 / 4 = 1 из геометрических размеров фермы.

N_1-14 = 25 кН.

3. Метод сечений.

Усилия в стержнях 5-6,5-11,7-11,10-11 определяем спосо­бом рассечения (метод Риттера). Для определения усилий в стержнях 5-6 и 5-11 рассекаем ферму сечением n- n (рис. 5.13.).

Рассматриваем равновесие одной отсеченной части фермы. Лучше рассматривать правую от сечения часть, так как на нее действует меньше сил.

Действие левой отброшенной части фермы на правую за­меним усилиями в рассеченных стержнях. Усилия направляем от узлов, предполагая стержни растянутыми. Усилие в стерж­не 5-6 определяем способом моментной точки. Этой точкой является узел 11.

Составляем уравнение моментов всех сил, действующих на данную часть фермы относительно точки 11.

Рис. 5.13. Равновесие правой части фермы (сечение n- n)

∑M₁₁=0

N_5-6·h - F·d + V_B ·2d = 0

N_5-6 = (F·d - V_B ·2d) / h = (10·4 – 25· 2 ·4) = - 40 кН.

Знак минус указывает на то, что стержень 5-6 - сжат.

Усилие в стержне 5-11 способом моментной точки опреде­лить нельзя, т.к. положение ее неизвестно (точка пересечения стержней 5-6 и 11-12 находится в бесконечности). Поэтому для определения усилия N_5-11 используем способ проекций.

Спроектируем все силы, действующие на правую часть фермы, на вертикальную ось. Составим уравнение равнове­сия:

ΣFу = 0;

N_5-11·sinα - F- F + V_B = 0

N_5-11 = (2 F - V_B) / sinα₁

sin α₁ = tg α₁ / (√ 1 + tg² α₁) = 1 / 1,41

N_5-11 = - 7,05 кН (стержень 5-11 сжат).

Для определения усилий в стержнях 7-11 и 10-11 рассечем ферму сечением m-m и рассмотрим равновесие правой отсе­ченной части (рис.5.14.).

Рис. 5.14. Равновесие правой части фермы (сечение m- m).

Для определения усилия в стержне 10-11 используем спо­соб моментной точки. Такой точкой является узел 7. Со­ставляем уравнение моментов относительно точки 7.

∑M₇ = 0

N_10-11 ·h - V_B ·d = 0

N_10-11 = V_B ·d / h = 25· 4 / 4 = 25 кН (растянут)

Для определения усилий в стержне 7-11 используем способ проекций. Спроектируем все силы на вертикальную ось и со­ставим уравнение:

ΣFу=0;

Проектируя на вертикальную ось все силы, тем самым ис­ключаем из уравнения проекций два усилия N_6-7 и N_10-11, и в уравнение входит только одно неизвестное усилие:

N_7-11 ·cosβ – F + V_B = 0

N_7-11 = (F - V_B) / cosβ

cosβ = 0,707

N_7-11 = (25 – 10) / 0,707 = 21,15 кН (стержень 7-11 растянут).

ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала...

ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры...

Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? - задался я вопросом...

ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между...

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: