|
|
Сборник задач по курсу КСЕ (ч.1. Физика)Раздел 1. Механика 1.1. Сколько времени займет перелет Земля-Альфа Центавра на звездолете со скоростью 0,9с при условии разгона до этой скорости с ускорением 2q. (c = 300000 км/с; q = 10м/с2, L = 4,3 световых года). Решение. З L0 α - Центавра
t0 =
1 год = 31,5 · 106с. 1 св.год = 31, 5 · 106 · 3 · 105 км = 1013км ║ t0 = Tобщ. = t0 + 2tp = 4,4 + 0,83 ≈ 5,2 г. 1.2. Каков «выигрыш» во времени в звездолете? (использовать данные задачи 1.1). Решение. Если ∆t3 = 4,4 г. = t0,то ∆ tp = 4,4 · 0,43 = 1,9 г. «Выигрыш» = 4,4 – 1,9 = 2,5 года. Если в «оба» конца, то по часам ракеты пройдет: (10 мес. + 1,9) · 2 = 5,5 лет, а по часам землян: 5,2 · 2 = 10,4 г., т.е. на 5 лет больше. 1.3. Какова может быть мощность звездолета? (Масса звездолета около 10 тыс.тонн, конечная скорость Vp = 0,9 c, время разгона до этой скорости определяется с учетом ускорения 2 q). Решение. 1) Зная конечную скорость V p = 0,9 c при условии a = 2 q, находим по формуле Vp = atp, tp = 0,9 c/2 q = 0,9 · 3 · 10 8/20 = 1,35 · 107c. 2) По формуле P = E/tp, где E = mv2/ 2, находим: P = 1.4. Какова мощность всех источников энергии на Земле? Соотнести ее с мощностью звездолета. Решение. Известно, что годовое выделение энергии на всех ГЭС, ТЭЦ, АЭС и т.п. составляло в 2000 г около 100 млрд. тонн условного топлива (q = 7000 ккал/кг, т.е. 7 ∙ 103 ∙ 4200 дж/кг ≈ 3 ∙ 107дж/кг). Общее количество энергии составляет: 3 ∙ 107 · 1014 = 3 · 1021дж. Мощность равна 3 · 1021/31,5 · 106 = 1014вт = 1011Квт. Полагая, что мощность звездолета 300 · 1011 Квт, видно, что она в 300 раз больше. Таким образом, создание звездолета пока нереально. 1.5. Как часто Земля «встречается» с другими звездами? (Период обращения Солнца вокруг центра нашей Галактики около 250 млн. лет; расстояние от Солнца до центра Галактики около 30 тыс. световых лет; среднее расстояние между звездами в Галактике около 10 парсек; 1 парсек = 3,26 световых года). Решение. 1) Оценка орбитальной скорости Солнца Тогда Vc = 2) Зная Vc, определим время τ, необходимое для преодоления расстояния в 10 парсек. Таким образом, за время существования цивилизации (5 – 10 тыс. лет) этого не происходило. С момента появления человека (около 2 млн. лет назад) мимо Земли могли «пролететь» не более 50 звезд. 1.6. Сколько людей возможно будет на Земле через 1000 лет? (В 1700 г. землян было 500 млн., в 1900 г. – 1,6 млрд., в 2000 г. – 6 млрд.). Решение. «Коэффициент размножения» в период с 1700 по 1900 гг (200 лет) равен 1,6 за 100 лет, а в период с 1900 по 2000 гг – 6/1,6 ≈ 3,75, т.е. в среднем за 300 лет: (3,75 + 1,6): 2 ≈ 2,7. Предположим, что этот коэффициент q = 2. Тогда, используя формулу для членов геометрической прогрессии an = a1qn-1, где а1 - первый член, равный 6 млрд., n – число столетий (1000 лет = 10 столетий). В результате получаем: a (3000 г) = 6 ∙ 29 = 6 ∙ (23)3 = 6 ∙ 83 = 6 ∙ 8 ∙ 64 ≈ 3 ∙ 1012. Таким образом, число людей может возрасти в 3 ∙ 1012/ 6 ∙ 109 = 500 раз. Замечание. Если считать, что каждую секунду на Земле умирает 2 чел., а рождается 3,5 чел., то прирост составляет в год: 1,5 ∙31,5 ∙ 106 ≈50 млн., а за 1000 лет составит 50 млрд., т.е. увеличится не более чем в 10 раз. (Ресурсы планеты смогут «прокормить» не более 20 млрд. чел.). Поэтому придется лететь в другие миры. 1.7. Каково гравитационное воздействие планет на человека? (Массы планет по отношению к Земле равны: Меркурия – 0,06; Венеры – 0,95; Марса – 0,64; Юпитера – 318; Сатурна – 95; Урана – 15; Нептун – 17,3. Масса Земли равна 6 ∙ 1021 тонн). Решение. Пользуясь формулой Если взять данные для самой крупной планеты Юпитера, то при m ≈ 70 кг получаем:
Для деформации атома водорода в молекуле воды (человек на 65% состоит из воды, а мозг – на 80%) потребуется энергия E0 = F ∙ ∆ℓ‚ где ∆ℓ ~ 10-10м (диметр атома водорода). Получаем, что E0 = 2,2 · 10-5·10-10 = 2 · 10-15дж. Энергия связи электронов в водороде равна 5 эв = 5 ·1,6 ·10-19дж.= 8 ∙ 10-19дж. Таким образом, Юпитер сможет «сдвинуть» в человеке около 2 · 10-15/8 · 10-19 ≈ 2500 атомов (в человеке молекул воды около 15 ∙ 1026!). 1.8. Каково воздействие Луны на человека? (Масса Луны в 81 раз меньше массы Земли, а расстояние до Луны – 384 тыс. км). Решение. По закону всемирного тяготения получаем, что
Сравнивая результат с задачей 1.7 видим, что Fл / Fю ≈ 100 раз, т.е. «сдвинется» около ¼ млн. атомов водорода. 1.9. Каково воздействие Луны на земную кору? (БСЭ, т.9, с.476-494 – статья о Земле: Мк = 2,8 ∙ 1022кг; М3 = 6 ∙ 1021т, Rз-л = 384000 км; R3 = 6370 км). Решение 1) Оценить массу земной коры, зная ее толщину (≈70 км), плотность (≈3т/м3), можно по формуле MK= ρк ∙ VK, где VK = 4πR
Видно: MK = 12π ∙ 1034 π · (6370 · 103)2 · 70 · 103 = 37,6 · 7 · 40,6 · 1019 ≈ 1023кг.
2) 3)По 2-му закону Ньютона:
За 20 сек. земная кора поднимется на
Почему за 20 сек.? Это то время, за которое проекция Луны «проходит» по поверхности Земли около 9 км, что приблизительно совпадает с дальностью горизонта, определяемой по ф-ле:
1.10. Каково гравитационное воздействие на человека Солнца? (Мс = 2 · 1030 кг; R = 1 а.е.). Решение. Если считать массу «стандартного» человека равной 70 кг, то
1.11. Каково гравитационное воздействие на человека одной из звезд зодиакальных созвездий? (Ближе всех β Близнецов – 10,7 пс; ее масса больше солнечной в 32 раза; Мс = 2 · 1027т). Решение.
1.12. Какова величина 1-й и 2-й космической скорости для планет Солнечной системы? (Массы планет приведены в задаче 1.7). Решение. Известно, что Найдем VI и VII для Земли.
VII = 11км/с. 1.13. Вычислить ускорение силы тяжести для Луны и других планет Солнечной системы (их массы см. в задачах 1.7). Решение. Из соотношения 1.14. Провести анализ данных о НЛО, сбитом над пустыней Калахари в ЮАР в 1990 г. (см. газету «Комсомольская правда» от 22.03.90). Решение. 1) Скорость объекта составляла по данным радаров 5746 морских миль в час. Так как 1 мор.м. = 1,8 км, то V0 = 5746 ∙ 1,8 км/ч = 10343 км/ч = 2,9 км/сек., т.е. скорость «космическая». 2) После обстрела лазерной пушкой объект стал падать и за tп = 1мин. потерял 3000 футов высоты. 1фут.= 0,3м. Тогда ∆h = 3000 · 0,3 = 900м. Ускорение падения 3) Затем объект упал. С какой высоты? Допустим, что с высоты около Н = 10 км. К моменту падения его скорость была равна V1 = V0 – antп = 2,9 км/с – 0,5 · 60 м/с = 2,9 – 30 · 10-3км/с = 2,9 – 0,03 ≈ 2,8 км/с. Время свободного падения:
Скорость падения в конце составила VK = V1 + qt0 = 2,8 4) Оценим энергию удара (масса объекта была оценена в 50 тонн).
5) Оценим силу удара, считая, что объект погрузился в почву за τ0 = 10 сек. Ускорение «торможения» при ударе
6) Оценим температуру нагрева объекта, считая, что 40% энергии объекта при ударе превратилось в теплоту. Q = 0,4 EK = mc ΔT, где m = 50т, c – удельная теплоемкость самого тугоплавкого материала (типа титана или вольфрама) составляет с ≈ 500 дж∕кг ∙ град. Тогда: При такой температуре относительное удлинение деталей объекта (дверей, которые потом, якобы открылись) составит:
Общий вывод: живые существа, которые, якобы вышли из НЛО, не смогли выдержать таких перегрузок при ударе и температуру.
Раздел 2. Элементы астрометрии 2.1. Установить основные элементы небесной сферы. Рассмотрим определения основных элементов небесной сферы (см. учебники по астрономии для школы или вуза). 1. Небесной сферой называют сферу произвольного радиуса с центром в точке наблюдения, на которую проецируются (мысленно) небесные объекты.
Небесный меридиан Z (зенит)
(южный Z′ (надир) полюс)
Рис.1. Элементы небесной сферы. 2. Линия, проходящая через точку наблюдения и совпадающая с линией отвеса, называется отвесной линией ZZ′. Точка пересечения отвесной линии со сферой, что над наблюдателем, называется зенитом, а противоположная ей – надиром. 3. Плоскость, перпендикулярная отвесной линии ZZ′, называется плоскостью математического горизонта, а линия пересечений ее со сферой – линией математического горизонта. Она проходит через точки горизонта: юга (S′), севера (N), запада (W) и востока (О). 4. Линия, соединяющая точки севера и юга (NS), называется полуденной линией (определяется в момент истинного полдня по наикратчайшей тени от гномона – шеста высотой h, если длина тени в этот момент равна ℓ, то высота Солнца (в угловой мере) равна arctq h/ℓ. 5. Линия, вокруг которой происходит видимое вращение небесной сферы с востока на запад (обусловлено вращением Земли в обратном направлении), называется осью мира (РР′), а точки ее пересечения со сферой – полюсами мира (Р – северный полюс, «совпадающий» с Полярной звездой (α Малой Медведицы). Под северным полюсом мира находится точка севера N. Ось мира наклонена к плоскости горизонта под углом, равным широте пункта наблюдения φ, т.е. углом PON = φ. Это видно из рисунка 2. Здесь: ЭЭ′ - экватор Земли, относительно которого отсчитывается широта φ; NS - линия горизонта на широте φ; ZZ′- отвесная линия; ПсПю – ось Земли (линия, соединяющая северный – Пс и южный – Пю географические полюса; РР′ - ось мира, которая всегда параллельна Земной оси; О – точка наблюдения; О1 – центр Земли; ОО1 – радиус Земли).
6. Плоскость, проходящую через три точки – P, Z и O, называют плоскостью небесного меридиана (он аналогичен земному меридиану, проходящему через географические полюса и пункт наблюдения с долготой λ). 7. Круг, проходящий через точки ZPNS, называется небесным меридианом. 8. Линия QQ PP′ называется небесным экватором (его плоскость параллельна плоскости земного экватора). 9. Светило, проходящее через небесный меридиан над точкой S, считается в верхней кульминации, а над точкой N – в нижней. 11. Высоты светил в моменты кульминаций определяются величиной дуг небесного меридиана: hS и hN. Их положение указывается точками М1 и М1′, М2 и М2′ и т.д. Линии типа М М′ - небесные параллели (они аналогичны земным параллелям на разных широтах). Общий рисунок выглядит так:
δ3 hN – дуга M2′N
M1′ Q′ ′ P′ M3′ Z′
Рис.3. Модель небесной сферы. [БСЭ, т.17.с.388-390] 11. Дуга QМ1 - склонение объекта М1 (δ >0), дуга QМ3 – для объекта М3 (δ3 < 0). 12. Дуга М1Z - зенитное расстояние для М1 и т.п. 2.2. Определить высоту светила в моменты кульминаций на известной широте φ. Склонение δ (δ>0 и δ<0). Решение. Из рис. 3 следует: hS (M1) = (90 - φ) + δ1 (1); hS (M3) = (90 - φ) – δ3 (2) hN (M2) = δ2 - (90 - φ) (3). 2.3. Установить условия наблюдения светил в зените, как незаходящие и не- восходящие. Решение. Из рис.3 следует: - если Z = 0, то φ = δ, (4) т.е. в зените кульминируют те светила, склонение которых численно равно широте пункта наблюдения (еще один способ определения φ) - если hN ≥ 0 (незаходящее светило), то δ > 90 – φ, (5) - если hS < 0 (невосходящее), то │δ│ > 90 - φ (6) (склонение < 0). 2.4. Определить максимальную высоту Солнца на широте г.Ижевска в дни равноденствий (20.03 или 21.03 и 23.09) и солнцестояний (22.06 и 21.12 или 22.12) (склонение Солнца в эти дни равны 0, + 230,5 и – 230,5; φИжевска = 56050′ ≈ 570). Решение. Используя формулу (1) из задачи 2.2, находим: - для 21.03 и 22.09, когда δ = 0 hS = 900 – 570 = 330 - для 22.06, когда δ = + 230,5 hS = 330 + 230,5 = 560,0 - для 22.12, когда δ = - 230,5 по ф-ле (2) hS = 330 – 230,5 = 90,5 ≈ 100. 2.5. На каких широтах начинаются «белые ночи»? Решение. Считается, что если в нижней кульминации глубина погружения Солнца менее 6050′, то ночи «белые». Из ф-лы (3) следует: δС - (90 -φ) ≥ 70 φ ≥ 830- δС (7) 22.06. δС = 230,5 и в этот день «белые ночи» наступают на всех широтах севернее 830 – 230,5 = 590,5, т.е. севернее Ленинграда (СПб). 21.03. и 22.09., когда δС = 0 – на широтах ≥ 830. В другие дни года они всегда бывают севернее 600 [см. ф-лу (7)]. 2.6.На каких широтах наступает «полярный день», т.е. Солнце не заходит? Решение. Для «полярного дня» hN ≈ -10 (за счет рефракции). Тогда из формулы (3) получаем δС - (90 -φ) ≥ - 10, т.е. δС + φ ≥ 89 (8). 22.06., когда δС = + 230,5 φ ≥ 890 – 230,5 ≥ 660,5, т.е. за северным полярным кругом. На северном полюсе (φ = 90): δС ≥ - 10, т.е. более полугода. 2.7. Каковы условия наступления «полярной ночи», когда Солнце не восходит? Решение. Из рисунка 3 видно, что если hS ≤ - 10 (за счет рефракции), то Солнце не видно. Из формулы (2) следует: (90 - φ) - |δС| ≤ - 10 |δС| ≥ 910 – φ; φ ≥ 910 - |δС| (9) 22.12, когда δС = - 230,5, для φ ≥ 670,5. Для северного полюса (φ = 900) |δС| ≥ 10, т.е. чуть меньше полугода будет ночь.
2.8. Как определить продолжительность «белых ночей» на широте φ? Решение. Из формулы (7) следует, что должно выполняться условие δС ≥ 830 - φ (10). Если φ = 600 (СПб), то δС ≥ 230. |δС│max = 230,5. Солнце в среднем за 3 месяца (с 21.03. по 22.06.) увеличивает свое склонение на 230,5, т.е. за 1 день на 15′, а на 10 – за 4 дня. Однако вблизи точек солнцестояний изменение склонения Солнца меньше 15′ и составляет около 5′. Поэтому интервал значений δС от 230 до 23 0,5 (перед солнцестоянием) и от 230,5 до 230 (после 22.06) общей дуги в 10 Солнце проходит около 2 недель. Поэтому в СПб белые ночи начинаются за неделю до 22.06 и длятся потом еще с неделю. Для широты, например, северного полярного круга (660,5) из условия (10) получаем: δС ≥ 830 – 660,5 ≥ 160,5. По астрономическому ежегоднику следует определить, начиная с какой даты склонение Солнца превысит величину + 160,5 и когда после 22.06 оно станет меньше + 160,5. Если считать, что ∆δС ≈ 15′⁄день, то δС = + 160,5 наступит спустя 2 месяца после 21.03, т.е. продолжительность «белых ночей» составит около 4 месяцев. 2.9. Как определить продолжительность «полярного дня» на широте φ? Решение. Из формулы (8) следует, что должно выполняться условие: δС ≥ 890 - φ, причем, δС всегда меньше 230,5. Решая неравенство 230,5 ≥ δС ≥ 890 - φ получаем, что это возможно только на широтах > 660,5. Например, для Мурманска (φ = 680,5) получаем: δС ≥ 890 – 680,5 ≥ 200,5. Склонение Солнца от 200,5 до 230,5 и от 2305 до 200,5 будет изменяться около месяца (в общей сложности), а даты можно определить по астрономическому ежегоднику (за любой год), где приводятся значения δС на каждый день. 2.10. Как определить продолжительность «полярной ночи» на широте φ? Решение. Из условия (9) следует, что 230,5 ≥ |δС| ≥ 910- φ, т.е. это возможно для φ ≥ 67,50. Если рассмотреть г. Мурманск, то δС ≥ 910 – 680,5 ≥ 220,5. Видно, что полярная ночь будет короче полярного дня на целую неделю. Примечание. Для более точного решения задач типа 2.8, 2.9 и 2.10 необходимо воспользоваться астрономическим ежегодником (для любого года), в которых приведены значения склонения Солнца (δС) для каждого дня года. В таких ежегодниках приводятся условия наблюдения планет, солнечных и лунных затмений, комет, звездных дождей и др. В астрономических справочниках (постоянная часть) приводятся сведения (склонения) большинства звезд всех 88-и созвездий, ряда Галактик и др. астрономические сведения. 2.11. Какое время показывают наши часы? Ответ. В России – декретное (+1 час) время N –го часового пояса (Tд). Поясное время (Tп) N –го пояса равно мировому (T0 – время нулевого меридиана вблизи Гринвича под Лондоном) + номер пояса: Tп = T0 + Nч (I). Время 2 –го пояса + 1ч называется московским. Поясное время – среднее солнечное время, единое в пределах часового пояса (всего 24 часовых пояса шириной в 150, т.е. 3600: 24 = 150). 2.12. Когда наступает истинный полдень? Решение. Расчетная формула имеет вид: Тд = (12ч + ε) + (Nч – λч) + 1ч декр., (II) где ε - уравнение времени, учитывающее разность между истинным или средним солнечным временем [БСЭ, т.27,с.53], Nч - номер часового пояса (в часах), λч - долгота пункта (в часах: 150 = 1ч,10 = 4м, 1′ = 4с). Если наблюдение летом, то добавляется еще 1 час (летнее время). Приведем некоторые значения ε: 16.04, 14.06, 01.09 и 25.12 ε = 0, εmax = + 14м (12.02); εmin = - 16м (04.11). ε01.01 = + 4м (график зависимости ε от дат года приведен в БСЭ, т.27.с.53). Пример 1. Долгота Ижевска 530 10′ = 3ч32м40с ≈ 3ч33м. (λУдмуртии Є [510 10′; 540 26′]; φЄ [550 10′; 580 38′]) Nч = 3ч. (Nч - λч + 1ч) = 3ч – 3ч33м +1ч = 27м. Итак, часы показывают в истинный полдень на долготе Ижевска (12ч27м + ε) (III) Если ε = 0, то зимой около 12ч30м, а летом – около 13ч30м. 2.13. Когда наступает истинный Новый год? Решение для Ижевска, где Nч - λч + 1ч = 27м. ε (01.01) = + 4м. По формуле (II) получаем: Тд = 24ч + 4м + 27м = 0ч31м. Если λ другая, то вместо формулы (II) использовать формулу Тд = 1ч 4м + (Nч - λч) (III). Если, например, Nч = λч, то Тд около часа ночи. Примечание. Формулу типа (II) можно использовать для определения долготы пункта наблюдения (λ), если известна величина ε (в день наблюдения) и номер часового пояса в момент истинного полдня (тень от шеста – гномона совпадает с полуденной линией). 2.14. Какую линейную скорость имеет г. Ижевск? (φИж = 56050′; cos φ = 0,55; R3 = 6370 км) Решение. Из рис.3 следует, что V = ωr, где r - радиус вращения г. Ижевска (и любого пункта на Земле) на широте φ, который равен r = R3 · cosφ, где R3 - радиус Земли. Т.к. ω =
Рис.3 |

|
На экваторе ЭЭ′ получаем: VЭ = Vu/cosφ = 464 м/с.
Поэтому в зоне экватора выгодней запускать ИСЗ, т.к. «выигрыш» может составить до 200 м/с (для Байконура).
Раздел 3. Электричество и магнетизм
3.1. А.Чумак утверждает, что выступая по телевидению, он сможет «заряжать» воду в сосуде перед экраном телевизора. Возможно ли это?
Ответ (аргументированный). Частота телевизионного канала в метровом диапазоне 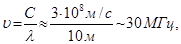 а частота звука (речи человека) не более 20 Кгц (средняя около 1 Кгц), т.е. в несколько тысяч раз меньше и поэтому речь человека не может модулировать электромагнитные волны (в любом диапазоне). Кстати, видеокамере все равно кто перед ней находится: телеведущий или экстрасенс. Процесс трансляции одинаков.
а частота звука (речи человека) не более 20 Кгц (средняя около 1 Кгц), т.е. в несколько тысяч раз меньше и поэтому речь человека не может модулировать электромагнитные волны (в любом диапазоне). Кстати, видеокамере все равно кто перед ней находится: телеведущий или экстрасенс. Процесс трансляции одинаков.
Термин «заряжать воду» означает, что в ней появились дополнительные заряды (ионы или электроны), что возможно только при ионизации молекул Н2О. А.Чумак утверждает, что он может изменить проводимость воды на 10 микроампер, даже находясь на своей даче, а вода – за несколько километров. В прессе были сообщения о его последователях, которые, якобы, изменяли проводимость воды на 7200 микроампер! Возможно ли такое?
Известно, что электрический ток – это направленное движение зарядов и 1 мкА = 10-6А, а 1А = 1 Кул/сек. Заряд в 1 Кулон создают 1/1,6 ∙ 10-19 = 6,2 ∙ 1018 электронов, заряд одного из них и равен 1,6 ∙ 10-19К. Таким образом, для увеличения проводимости на 10 мкА необходимо ежесекундно генерировать 6 ∙ 1013 = 60 триллионов электронов! А для величины в 7200 мкА – 7,2 ∙ 10-3 ∙ 6,2 ∙ 1018 = 450 ∙ 1014 = 45000 триллионов!
Для освобождения из молекулы воды одного электрона требуется энергия 4,77 Эв (энергия связи электрона в атоме водорода) и чтобы создать 4,5 ∙ 1016 электронов нужно воде сообщить энергию 4,5∙1016 ∙ 4,77 ∙1,6 ∙ 10-19дж=3,4∙10-2дж/с, т.е. иметь мощность около 0,03 вт = 30 мвт, что соизмеримо с мощностью радиотелефонов. Если эту энергию выделяет мозг человека (А.Чумака или его учеников), то за год работы (31,5 млн. сек) он выделяет энергию в 3,4 ∙ 10-2 ∙ 31,5 ∙ 106 ≈ 106 дж, что хватило бы для нагревания его мозга (80% массы мозга – это вода; масса мозга человека около 1,5 кг; воды в нем около 1,2 кг; удельная теплоемкость воды 4200 дж/кг) на ∆Т = Q/с ∙ m = 106/4200 · 1,2 ≈ 2000 (!), а за неделю его работы – на ≈ 40, что было бы заметно!
Таким образом, по законам биологии и на основании расчетов «феномена Чумака» нет! Световое же излучение экрана не способно ионизировать воду и тем более изменять структуру мазей в тюбиках, куда свет и не проникает. Легко показать, что энергия световых лучей (средняя длина их около (3900 + 7500): 2 = 5700 А (ангстрем) = 5,7 ·103 · 10-10м = 5,7 · 10-7м, а средняя частота  = 3 · 108/5,7 ∙ 10-7· 5 ·1014Гц. Тогда средняя энергия равна:
= 3 · 108/5,7 ∙ 10-7· 5 ·1014Гц. Тогда средняя энергия равна:  - h v = 6,62 · 10-34 · 5 ·1014 ≈ 3 ·10-19дж = 3 · 10-19/1,6 · 10-19 ≈ 2 эв, а энергия связи электронов около 5 эв, т.е. фотоэффект невозможен.
- h v = 6,62 · 10-34 · 5 ·1014 ≈ 3 ·10-19дж = 3 · 10-19/1,6 · 10-19 ≈ 2 эв, а энергия связи электронов около 5 эв, т.е. фотоэффект невозможен.
«Мягкое» рентгеновское излучение, возникающее в телевизионной трубке (ускоряющая разность потенциалов между катодом и анодом в цветном телевизоре около 20 кэв и электроны приобретают энергию E = q ∆U ≈ 1,6 ∙ 10-19 ∙ 20 · 103 ≈ 3 ∙ 10-15 дж = 3 ∙ 10-15/1,6 ∙ 10-19 ≈ 2000 эв; λ = с/ν = hc/Е = 6,6 ∙ 10-34 ∙ 3 ∙ 108/3 ∙ 10-15 ≈ 6,6 ∙ 10-11м = 0,7 Ангстрема) легко поглощается стеклом экрана и воздухом.
Для сравнения – энергия излучения медицинского рентгена около 200 Кэв,
т.е. в 200 раз больше (см. также задачу 4).
3.2. Насколько реален «гроб Магомета»? (гробом Магомета называют металлический гроб, висящий в воздухе).
Решение. Если по гробу длиной ℓ пропускать ток в I A в поле с индукцией B, то возникает сила Ампер величиной F = L ∙ ℓ ∙ B sin α, (1) где α – угол между векторами I и B (будем считать, что α = 900). Сила Ампера должна уравновесить вес гроба P = mq (2). Из равенства соотношений (1) и (2) следует: IB = mq/ℓ(3).
Если положить, что ℓ = 2 м, а m = 100 кг, то I B = 500 А ∙ Тл (4).
Допустим, что по гробу идет ток I = 100 A. Тогда в зазоре Δh = 2 м (высота пещеры, где, якобы, висел гроб Магомета), точнее на расстоянии х = 1м (от пола или потолка) необходимо создать индукцию В = 5,0 Тл (Тесла).
Если гроб поместить под соленоидом радиуса R = 0,5 м (1 м – ширина гроба), то при пропускании через него тока IC на расстоянии х от его торца возникает индукция  (5)
(5)
Здесь: μо = 4П ∙ 10-7гн/м; R = 0,5 м, х = 1 м.
Тогда  (6)
(6)
Из (6) следует: 10-7LC · μотн = 5,0. Тогда LC μотн = 5 · 107. (7)
Если LC = 100 A, то μотн должно быть не менее 0,5 · 106.
Это возможно, если гроб будет сделан из супермаллоя (5 % молибдена, 79% - никеля, остальное – чистое железо; для такого сплава μотн ≈ 106).
Таким образом, в наше время создать такой эксперимент технически возможно, но вряд ли это было сделано 1000 лет назад.
3.3. Во сколько раз «куловские силы» больше гравитационных?
Решение. Сопоставим эти силы, возникающие в атоме водорода (заряд ядра и электрона q = 1,6 ∙ 10-19К; масса электрона me = 9 ∙ 10-31кг, протона – в 1836 раз больше; радиус атома
r = 10-10м; γ = 6,67 · 10-11м3/кг · сек2; εо = 8,85 · 10-12 ф/м).
Сравнивая выражения  и
и 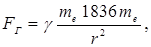 получаем:
получаем: 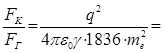

 (!)
(!)
3.4. Каково отталкивание двух шаров, заряженных по 1 Кулону на расстоянии в 1 м?
Решение. 
3.5. Какая энергия может быть заключена в грозовом облаке?
Решение. Будем считать, что система «облако – поверхность Земли» образуют обкладки плоского конденсатора площадью S с зазором в h (высота тучи), а разряд молнии длится τ ≈ 0,001 с. Задаваясь значениями S ≈ 10км х10км = 108м2 и h ≈ 1000 м, по ф-ле С = εε0 S/h (ε0 = 8?85 · 10-12 ф/м) находим, что С = 8,85 · 10-12 · 108/103 ≈ 10-6 ф. (ε = 1 для воздуха; 8,85 ≈ 10).
Зная пробивное напряжение воздуха, равное 30 Кв/см, находим, что «предпробивное» напряжение между тучей и землей составляет Uпр = 3 ∙ 106 ∙ 103 ≈ 3 ∙ 109 в. Величина тока в канале молнии составляет IM = Q/τ, где Q можно найти по ф-ле С = Q/ Uпр. Получаем. Что Q = С · Uпр = 10-6 · 3 · 109 ≈ 3000 Кулон.
Тогда IM = 3 ∙ 103/10-3 ≈ 3 ∙ 106 A. Мощность P = IMUм = 3 ∙ 106 ∙ 3 ∙ 109 ≈ 10,0 ∙ 1012 Квт = 10 триллионов киловатт! (На Земле ежегодно происходят десятки тысяч гроз).
Примечание. Если считать, что разряд молнии растекается и «уходит» в землю в радиусе 10 м, то поверхностная плотность тока составит величину I/πR2 ≈ 3 ∙ 106/300 ≈ 104 A/м2. Если площадь ступней человека (25 х 8) ∙ 2 см2 = 400 см2, то через них пройдет ток ~ 104 ∙ 400 ∙ 10-4 ≈ 400 А, что является смертельной величиной. Даже в радиусе 100 м от места удара молнии он будет ≈ 4 А, что также опасно для жизни.
Раздел 4. Ядерная физика
Известно, что источником энергии звезд, в т.ч. и Солнца, являются термоядерные реакции слияния легких ядер, например, водорода в гелий и т.д.
4.1. Каковы запасы энергии в водах мирового океана? (Общая масса воды на Земле составляет М = 1,5 ∙ 1015 т.; выделенные из стакана воды ядра дейтерия при их слиянии выделяют столько же энергии, что и при сжигании бочки бензина, теплотворная способность которого 11000 ккал/кг).
Решение. 1) Бочка бензина (200 л) при сгорании даст Фо = 200 ∙ 0,8 ∙ 11000 ∙ 4200 = 1,6 ∙11 ∙ 4,2 ∙ 108 дж = 74∙ 108 дж (здесь учтено, что плотность бензина 0,8 кг/л).
2) Кол-во стаканов воды в мировом океане составляет 1,5 ∙1018/0,2 = 75 ∙1017 (1 стакан – 200 г).
3) Общее кол-во энергии может составить:75 ∙ 1017 ∙ 74 ∙ 108 = 5,5 ∙ 1028 дж.
Если считать, что энергопотребление на Земле каждые 100 лет удваивается, то через n ∙ 100 лет оно составит: Qn = Qo 2n-1, где Qo = 3 ∙ 1021дж (см.задачу 1.6).
Задаваясь значением Q = 5,5 ∙ 1028, определим n – число столетий.
5,5 ∙ 1028 = 3 ∙ 1021 ∙ 2 n-1 ; 2 n-1 ≈ 2 ∙ 107. Отсюда n = 8, т.е. запасов энергии в водах мирового океана хватит как минимум на 1000 лет, а энерговооруженность планеты возрастет в 10 млн. раз! Если n – число тысячелетий, то запасов энергии хватит на 8 – 10 тыс. лет.
4.2. За сколько лет интенсивность излучения Солнца уменьшится на 10 %? (Постоянная солнечной радиации в современную эпоху составляет 2 кал/см2.мин – это на границе земной атмосферы; расстояние от Земли до Солнца около 150 млн. км; современное значение массы Солнца около 2 ∙ 1027тонн).
Решение. 1) Значение постоянной солнечной радиации в системе СИ равно: 2 ∙ 4,2/10-4 ∙ 60 = 1400 дж/м2сек.
2) Площадь сферы с радиусом «Земля - Солнце» равна:
S = 4π ∙ (150∙ 109)2м2 = 4π ∙ 225 ∙ 1020 = 2,8 ∙ 1023м2.
3) Общий поток энергии составляет (в сек.):
2,8 ∙ 1023 ∙ 1400 ≈ 2,8 ∙ 1,4 ∙ 1026 ≈ 4 ∙ 1026 дж/с.
4) По ф-ле Е = шс2 найдем «потерю» массы Солнца (в 1 сек.):
Δm = 4 · 1026/(3 ∙ 108)2 = 4,4 ∙ 109кг/с = 4,4 ∙ млн.т/сек.
5) Потеря 10 % нынешней массы Солнца произойдет за 

Если учесть, что возраст Солнца оценивается около 10 млрд.лет, то его еще «хватит» 1000 таких циклов.
4.3.Определить годовой расход U–235 на 1-й в мире АЭС (P=5000 квт, к.п.д.=17 %, при распаде одного ядра U–235 выделяется 200 мэв:1 эв =1,6·10-19 дж
Решение. Выделяемая энергия в реакторе АЭС составляет (Р/к.п.д.) · Т, где Т = 31,5 · 106сек (это год).
Получаем:  Для ее получения должно распадаться 9,3 · 1014/200 · 106 · 1,6 · 10-19 = 2,9 · 1025 ядер U – 235. Известно, что 1 г-атом U – 235, содержащий число Авагардо атомов (6 · 1023), имеет массу 235
Для ее получения должно распадаться 9,3 · 1014/200 · 106 · 1,6 · 10-19 = 2,9 · 1025 ядер U – 235. Известно, что 1 г-атом U – 235, содержащий число Авагардо атомов (6 · 1023), имеет массу 235


Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...

Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все...

ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между...

Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: