|
|
Физические и логические принципы работы компьютера. Базовые логические операции. Принцип выполнения программ.Люди, далекие от техники, часто смотрят на ЭВМ и др. цифровые электронные устройства, как на нечто таинственное и непостижимое. Тем не менее, все эти устройства работают в строгом соответствии с четкими логическими законами. Знание и понимание этих законов помогает в общении с компьютером. В основе всех выводов компьютера лежат три основные операции: «И», «ИЛИ», «НЕ». Иногда эти операции называют «тремя китами машинной логики». При записи логических выражений используется специальный язык, который принят в машинной логике. Основоположником мат. Логики является великий немецкий математик Готфрид Вильгельм Лейбниц. Он сделал попытку построить универсальный язык, с помощью которого споры между людьми можно было бы разрешать посредством вычислений. На заложенном Лейбницем фундаменте ирландский математик Джордж Буль построил здание новой науки – математической логики (Алгебры логики), которая в отличие от обычной алгебры оперирует не числами, а высказываниями. В честь Д. Буля логические переменные в языке программирования Паскаль в последствии назвали булевскими. Высказывание - это любое утверждение, относительно которого можно сказать истинно оно или ложно, т.е. соответствует оно действительности или нет. Таким образом, по своей сути высказывания фактически являются двоичными объектами и поэтому часто истинному значению высказывания ставят в соответствие 1,а ложному - 0. Например, запись А=1 означает, что высказывание А - истинно. Высказывания могут быть простыми и сложными. Простые -соответствуют алгебраическим переменным, а сложные являются аналогом алгебраических функций. Функции могут получаться путем объединения перемещенных с помощью логических действий. Самой простой логической операцией является операция «НЕ» (по другому её часто называют отрицанием, дополнением или инверсией и обозначают NOT X). Результат отрицания всегда противоположен значению аргумента. Логическая операция «НЕ» является унарной, т.е. имеет всего один операнд. В отличие от «НЕ», операции «И» (AND) и «ИЛИ» (OR) являются бинарными, т.к. представляют собой результат действий над двумя логическими величинами. Логическое «И» ещё часто называют конъюнкцией, или логическим умножением, а «ИЛИ» – дизъюнкцией, или логическим сложением. Часто в ВТ используют дополнительную логическую операцию “исключающее ИЛИ”(X XOR Y), которая отличается от «ИЛИ» только при X=1, Y=1.
Операция «И» имеет результат “истина” только в том случае, если оба операнда истинны. Операция «ИЛИ» “менее привередлива” к исходным данным. Она дает “истину” если значение “истина” имеет хотя бы один из операндов. В случае, когда справедливы оба аргумента одновременно, результат также истинный. В таблицах истинности указаны все возможные комбинации логических переменных Х и У, а также соответствующие им результаты операций. Таблица истинности может рассматриваться в качестве одного из способов задания логической функции. Операции «И», «ИЛИ», «НЕ» образуют полную систему логических операций, из которых можно построить сколь угодно сложное логическое выражение. Обработка информации в ЭВМ происходит путём последовательного выполнения элементарных операций. К ним относятся: установка - запись в операционный элемент(например, регистр) двоичного кода: прием- передача (перезапись) кода из одного элемента в другой; сдвиг- изменение положения кода относительно исходного; преобразование- перекодирование; сложение- арифметическое сложение или целых двоичных чисел- некоторые другие. Для выполнения каждой из этих операций сконструированы электронные узлы, являющиеся основными узлами цифровых вычислительных машин- регистры, счетчики, сумматоры, преобразователи кодов и т.д. В основе каждой из элементарных операций лежит некоторая последовательность логических действий. Например, операция сложения двух чисел: 3+6. Имеем: +110
На каждом элементарном шаге двум двоичным цифрам сопоставляется двоичное число (одно или двухзначное) по правилам: (0;0) Рассмотрим условные обозначения базовых логических элементов.
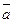 a a + b a a + b
« И » « ИЛИ» «НЕ» «X ИЛИ»
Простейшие логические элементы можно реализовать аппаратно. Это означает, что можно создать электронные устройства на транзисторах, резисторах и т.п, каждая из которых имеет один или два входа для подачи управляющих напряжений и один выход, напряжение на котором определяется таблицей истинности. На практике логическому ”да” (”истина”, или цифра 1) соответствует наличие напряжения, логическому “нет” (”ложь”, или цифра 0) – его отсутствие. В качестве примера применения логических элементов в ВТ возьмем устройство, называющееся сумматором. Его назначение - нахождение суммы двух двоичных чисел. Рассмотрим простейшее устройство, являющееся звеном сумматора – полусумматор - реализующий сложение двух одноразрядных двоичных чисел, которые обозначим А и В. В результате получается двухразрядное двоичное число. Его младшую цифру обозначаем S, а старшую, которая при сложении многоразрядных чисел будет перенесена в старший разряд, через Со (от английского Carry out-”выходной перенос”). Обе цифры можно получить по следующим логическим формулам: S= ( Черта над символом обозначает операцию NOT. Это легко проверить перебором всех четырех возможных случаев сочетания значений А и В, по таблице. Таблица истинности для полусумматора.
Мысленно объединим столбцы А, В и Со. Полученная таблица напоминает базовый элемент «И». Аналогично сравнив первые три столбца A, B и S с таблицей истинности для рассмотренных логических элементов, обнаружением подходящий для наших целей элемент «исключающее ИЛИ”. Таким образом, для реализации полусумматора достаточно соединить параллельно входы двух логических элементов.
Логическая схема полусумматора.

 A A  + +  B = S B = S
     B B
Co
А) с использованием лишь базовых логических элементов.
Б) с использованием “исключающего ИЛИ”.
При построении функциональных узлов КС используются элементы, которые реализуют базовую систему логических функций. Одним из таких базовых наборов является набор из трех функций: дизъюнкции (логическое ИЛИ), конъюнкции (логическое И) и отрицание (логическое НЕ). На рис. 2.1.2. показаны условные обозначения и значения выходного сигнала в зависимости от входных сигналов. Ноль изображается на диаграммах низким значением сигнала, а единица – высоким. Используя эти базовые элементы, строятся все функциональные узлы ЦВМ.

«логическое ИЛИ» «логическое И» «логическое НЕ»
Рис. 2.1.2. Базовая система логических элементов цифровых устройств   Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор...  Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем...  Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...  ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|