Похідна функції комплексної змінної
Похідною однозначної функції комплексної змінної  називається границя відношення називається границя відношення  , якщо , якщо  будь-яким способом наближається до нуля. Таким чином, будь-яким способом наближається до нуля. Таким чином,  . .
Функція, яка має похідну при даному значенні z, називається диференційовною при цьому значеннні z.
Функція  називається аналітичною в точці називається аналітичною в точці  , якщо вона має похідну в точці , якщо вона має похідну в точці  , а також в деякому околі цієї точки. Функція , а також в деякому околі цієї точки. Функція  називається аналітичною в області D, якщо вона має похідну в кожній точці цієї області. називається аналітичною в області D, якщо вона має похідну в кожній точці цієї області.
Якщо функція  диференційована в точці диференційована в точці  , то в цій точці існують частинні похідні , то в цій точці існують частинні похідні  , ,  , ,  , ,  , що відповідають умовам , що відповідають умовам  , ,  , які називаються умовами Коші-Рімана. , які називаються умовами Коші-Рімана.
Умови Коші-Рімана є необхідними та достатніми умовами диферен-ційовності функції  в точці в точці  . .
Похідна функції  виражається через частинні похідні функцій виражається через частинні похідні функцій  і і  за допомогою формул за допомогою формул
 . .
Похідні елементарних функцій  , ,  , cosz, sinz, lnz, arcsinz, arctgz, shz, chz знаходять за допомогою формул, що правильні для дійсного аргумента: , cosz, sinz, lnz, arcsinz, arctgz, shz, chz знаходять за допомогою формул, що правильні для дійсного аргумента:
 , ,  , ,
 , ,  , ,
 , ,  , ,
 , ,  , ,
 , ,  . .
Інтеграл від функцій комплексної змінної
Нехай однозначна функція  визначена і неперервна в області D, а С – кусково-гладка крива, яка лежить в області D. визначена і неперервна в області D, а С – кусково-гладка крива, яка лежить в області D.
Нехай  . Тоді . Тоді
 . .
Нехай С – кусково-гладка лінія, яка складається із гладких частин  ; тоді інтеграл по цій лінії можна визначити за допомогою рівності ; тоді інтеграл по цій лінії можна визначити за допомогою рівності  . .
Називатимемо область D однозв'язною, якщо будь-який контур, який лежить всередині області D, можна стягнути в точку, не виходячи за межі області D.
Якщо  – аналітична функція в однозв'язній області D, яка обмежена замкненим контуром С, а також в точках цього контуру, то – аналітична функція в однозв'язній області D, яка обмежена замкненим контуром С, а також в точках цього контуру, то  – теорема Коші для однозв'язної області. – теорема Коші для однозв'язної області.
Якщо  – аналітична функція в однозв'язній області D, то інтеграл не залежить від шляху інтегрування. – аналітична функція в однозв'язній області D, то інтеграл не залежить від шляху інтегрування.
Якщо  – аналітична функція в однозв'язній області D, яка містить точки – аналітична функція в однозв'язній області D, яка містить точки  і і  , то має місце формула Ньютона-Лейбніца , то має місце формула Ньютона-Лейбніца  , де , де  – будь-яка первісна для функцїі – будь-яка первісна для функцїі  , тобто , тобто  в області D. в області D.
Для знаходження первісної функції по відношенню до аналітичної функції  застосовуються звичайні формули інтегрування. застосовуються звичайні формули інтегрування.
Так, наприклад, формула інтегрування частинами має вигляд
 . .
Якщо крива С задана параметричними рівняннями  , ,  , причому початкова та кінцева точки точки кривої С відповідають значенням параметра , причому початкова та кінцева точки точки кривої С відповідають значенням параметра  , то , то  , де , де  . .
Розглянемо n +1 замкнених кусково-гладких ліній  , таких, що кожна із ліній , таких, що кожна із ліній  лежить поза решти інших і всі вони розміщені в середині лежить поза решти інших і всі вони розміщені в середині  . .
Множина точок, які лежать одночасно в середині  і поза і поза  , являє собою (n +1) – зв'язну область D, межа якої складається з ліній , являє собою (n +1) – зв'язну область D, межа якої складається з ліній  . .
Нехай  – аналітична функція в області D, а також на контурах – аналітична функція в області D, а також на контурах  . Тоді має місце рівність . Тоді має місце рівність
 – теорема Коші для багатозв'язної області (при цьому напрям обходу усіх контурів однаковий). – теорема Коші для багатозв'язної області (при цьому напрям обходу усіх контурів однаковий).
Якщо  – аналітична функція в області D, обмеженій кусково-гладким замкненим контуром – аналітична функція в області D, обмеженій кусково-гладким замкненим контуром  , ,  , то має місце рівність , то має місце рівність  — інтегральна формула Коші. — інтегральна формула Коші.
Ряди в комплексній області
 – степеневий ряд у комплексній області. – степеневий ряд у комплексній області.
Теорема Абеля. Якщо степеневий ряд  збігається при деякому значенні збігається при деякому значенні  , то він збігається абсолютно при всіх значеннях z, для яких , то він збігається абсолютно при всіх значеннях z, для яких  . Якщо ряд . Якщо ряд  є розбіжним при є розбіжним при  ,то він є розбіжним також при будь-якому значенні z, для якого ,то він є розбіжним також при будь-якому значенні z, для якого  . .
Область збіжності ряду  є кругом з центром у точці є кругом з центром у точці  , тобто ряд , тобто ряд  збігається при збігається при  , де , де  – радіус збіжності. Радіус збіжності можна також знаходити за формулою – радіус збіжності. Радіус збіжності можна також знаходити за формулою  . .  – ряд в комплексній області з від'ємними степенями. Такий ряд збігається в області – ряд в комплексній області з від'ємними степенями. Такий ряд збігається в області  , де , де  . .
Ряд Тейлора
Функцію  , однозначну і аналітичну в точці , однозначну і аналітичну в точці  ,можна розвинути в околі цієї точки в степеневий ряд Тейлора ,можна розвинути в околі цієї точки в степеневий ряд Тейлора  , коефіцієнти якого можуть бути знайдені за формулами , коефіцієнти якого можуть бути знайдені за формулами  , де , де  – коло з центром в точці – коло з центром в точці  , яке повністю лежить в околі точки , яке повністю лежить в околі точки  , в якому функція , в якому функція  аналітична. аналітична.
Найбільш важливі розкладання аналітичних функцій у ряд Тейлора в околі точки  : :
  ; ;
  ; ;
  ; ;
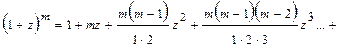
  ; ;
  . .
Ряд Лорана
Функцію  , однозначну і аналітичну в кільці , однозначну і аналітичну в кільці  , можна розвинути в цьому кільці в ряд Лорана , можна розвинути в цьому кільці в ряд Лорана
 , ,
коефіцієнти якого можуть бути знайдені за формулами 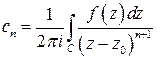 , де , де  – коло з центром в точці – коло з центром в точці  , яке повністю лежить всередині даного кільця. , яке повністю лежить всередині даного кільця.
Ряд  називається головною частиною ряду Лорана, ряд називається головною частиною ряду Лорана, ряд  називається правильною частиною ряду Лорана. називається правильною частиною ряду Лорана.
Нулі аналітичної функції
Нехай функція  є аналітичною в точці є аналітичною в точці  . Точка . Точка  називається нулем функції порядку n, якщо виконуються умови називається нулем функції порядку n, якщо виконуються умови  . .
Точка  тоді і тільки тоді є нулем функції порядку n функції тоді і тільки тоді є нулем функції порядку n функції  , коли в деякому околі цієї точки має місце рівність , коли в деякому околі цієї точки має місце рівність  , де функція , де функція  аналітична в точці аналітична в точці  і і  . .
Ізольовані особливі точки
Точка  називається ізольованою особливою точкою функції називається ізольованою особливою точкою функції  , якщо існує такий окіл цієї точки, в якому , якщо існує такий окіл цієї точки, в якому  є аналітичною всюди, окрім самої точки є аналітичною всюди, окрім самої точки  . .
Точка  називаєтьсяуcувною особливою точкою функції називаєтьсяуcувною особливою точкою функції  , якщо існує скінченна границя функції , якщо існує скінченна границя функції  в точці в точці  . .
Точка  називаєтьсяполюсом, якщо називаєтьсяполюсом, якщо  . .
Для того щоб точка  була полюсом функції була полюсом функції  , необхідно і достатньо, щоб ця точка була нулем для функції , необхідно і достатньо, щоб ця точка була нулем для функції  . .
Точка  називається полюсом порядку називається полюсом порядку  функції функції  , якщо ця точка є нулем порядку n для функції , якщо ця точка є нулем порядку n для функції  . У випадку n =1 полюс називається простим. . У випадку n =1 полюс називається простим.
Для того щоб точка  була полюсом порядку була полюсом порядку  функції функції  , необхідно і достатньо, щоб функцію , необхідно і достатньо, щоб функцію  можна було зобразити у вигляді можна було зобразити у вигляді  , де функція , де функція  аналітична в точці аналітична в точці  і і  . .
Точка  називається істотно особливою точкою функції називається істотно особливою точкою функції  , якщо в точці , якщо в точці  не існує границі. не існує границі.
Лишки функцій
Нехай точка  є ізольованою особливою точкою функції є ізольованою особливою точкою функції  . Лишком функції . Лишком функції  в точці в точці  називається число, яке позначається символом називається число, яке позначається символом 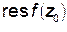 (або (або  ) і визначається таким чином ) і визначається таким чином  , де С – коло з центром в точці , де С – коло з центром в точці  достатньо малого радіуса такого, щоб коло не виходило за межі області аналітичності функції достатньо малого радіуса такого, щоб коло не виходило за межі області аналітичності функції  і не містило всередині інших особливих точок функції і не містило всередині інших особливих точок функції  . .
Лишок функції  дорівнює коефіцієнту при мінус першого степеня в лоранівському розвиненні дорівнює коефіцієнту при мінус першого степеня в лоранівському розвиненні  в околі точки в околі точки  : :
 . .
Лишок вуcувній особливій точці дорівнює нулю.
Якщо точка  є полюсом n -го порядку функції є полюсом n -го порядку функції  , то , то
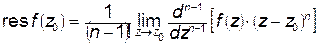 . .
У випадку простого полюса (n=1) лишок дорівнює
 . .
Якщо функція  в околі точки в околі точки  може бути зображена як частка двох аналітичних функцій може бути зображена як частка двох аналітичних функцій  , то , то  , ,
де  , тобто , тобто  —простий полюс функції —простий полюс функції  . .
Якщо точка  є істотно особливою точкою функції є істотно особливою точкою функції  , то для знаходження , то для знаходження 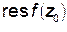 необхідно знайти коефіцієнт необхідно знайти коефіцієнт  у лоранівському розвиненні функції у лоранівському розвиненні функції  в околі точки в околі точки  ; це і буде ; це і буде 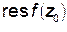 . .
Теорема Коші про лишки
Нехай функція  аналітична вобласті D, за винятком скінченного числа особливих точок аналітична вобласті D, за винятком скінченного числа особливих точок  , і аналітична на С – замкненій межі області D. Тоді має місце формула , і аналітична на С – замкненій межі області D. Тоді має місце формула  , денапрям обходу контуру Сдодатний (теорема Коші про лишки). , денапрям обходу контуру Сдодатний (теорема Коші про лишки).
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




