|
|
МетодЫ решения оптимизационной задачиСтр 1 из 5Следующая ⇒ МетодЫ решения оптимизационной задачи Курсовая работа включает в себя подавляющее большинство методов оптимизации, прочитанных в курсах «Методы оптимизации» и «Теория принятия решений». Каждый метод представлен в виде отдельной функции-члена класса. Все однотипные методы (в плане необходимых сведений для поиска) имеют одинаковое число аргументов. В большинстве своём - это начальная точка, погрешность максимальное количество шагов. В этом разделе представлены краткие описание методов оптимизации и применяемых математических формул. Сначала идут описания одномерных методов поиска, а затем многомерных.
Методы одномерной минимизации Метод Свенна - 1
Метод Свенна организует начальную локализацию минимума унимодальной функции, т.е. простой одномерный поиск с удвоением шага, критерием окончания которого является появление признака возрастания функции. Начальный этап. (1) задать произвольную начальную точку x0ÎRn (2) выбрать начальный шаг h=Dx=0,01 Основной этап Шаг 1. Установить направление убывания функции. Для этого взять x2=x1+h. Если f(x1) <f(x2), то поменять направление движения: h1=-h1 и взять x2=x1+h1. Шаг 2. Вычислить fk в точках xk+1=xk+hk, где k=2,3,4,…,m-1; hk=2hk-1 – движение с удвоением шага, до тех пор, пока не придём в точку xm такую, что f(xm)<f(xm-1). Шаг 3. Установить начальный интервал локализации минимума a1=xm-2 b1=xm
double swanna(double &h,double &x1,double &x2) { x2=x1+h; if (f(x2)>f(x1)) { h=-h; x2=x1+h; } while(f(x2)<f(x1)) { x1=x2; x2=x1+h; h=h*2; } return (x2); } Метод Свенна - 2
if (x1!=0) h=0.01*x1; else h=0.01;
if (proiz_f(x1)>0) h=-h; x2=x1+h; while (proiz_f(x2)*proiz_f(x1)>0) { x1=x2; x2+=h; h=2*h; } a=x1; b=x2; if (b<a) { x2=a; a=b; b=x2; } Метод Свенна - 3
Метод золотого сечения
Метод золотого сечения – это процедура одномерного поиска минимума на интервале [a1,b1] или [0,1]. На каждом шаге пробная точка lk или mk внутри текущего интервала локализации [ak,bk] делит его в отношении, постоянном для всех интервалов
Алгоритм ЗС-1 Начальный этап (1) Выбрать погрешность расчёта e=10-3¸10-7. Получить начальный интервал методом Свенна. (2) Вычислить стартовые точки l1=a1+0,382L1, m1=a1+0,618L1 (следует отметить, что золотые числа следует вычислять точно) (3) Принять k=1 – счётчик числа итераций Основной этап Шаг 1.Сократить ТИЛ рассмотрением 2-х ситуаций: (1) Если f(l)<f(m),то ak+1=ak bk+1=mk mk+1=lk lk=ak+1+0,382Lk+1 иначе ak+1=lk bk+1=bk lk+1=mk mk=ak+1+0,618Lk+1 (2) Положить k=k+1, Lk+1=|bk+1-ak+1| Шаг 2. Проверить критерий окончания поиска: если |ak+1-bk+1|£e - остановиться – минимум найден. Точнее фиксируем аппроксимирующий минимум как
double GSS(double a, double b) // golden section search - 1 { double tau1, tau2, lyambda, sigma, eps = 0.001; tau1 = (sqrt(5.0) - 1) / 2; // золотые числа tau2 = pow(tau1,2); lyambda = a + tau2 * abs(b - a); // начальные точки sigma = a + tau1 * abs(b - a); while (abs(b - a) > eps) // пока не достигнется нужная точность { if (f(lyambda) < f(sigma)) // определение направления сокращения { b = sigma; // сокращение интервала sigma = lyambda; lyambda = a + tau2 * abs(b - a); } else { a = lyambda; lyambda = sigma; sigma = a + tau1 * abs(b - a); } } return (lyambda + sigma) / 2; // середина интервала - аппроксимирующий минимум } Алгоритм ЗС-2 Начальный этап (4) Выбрать погрешность расчёта e=10-3¸10-7. Получить начальный интервал методом Свенна. (5) Вычислить стартовые точки l1=a1+0,382L1, m1=a1+0,618L1 (следует отметить, что золотые числа следует вычислять точно) (6) Принять k=1 – счётчик числа итераций Основной этап Шаг 1. Взять очередную пробную точку x2=ak+bk-x1, симметричную исходной и сократить ТИЛ рассмотрением 4-х возможных ситуаций: (1) Если (x1<x2) и (f(x1)<f(x2)) то b=x2; (2) Если (x1<x2) и (f(x1)>=f(x2)) то a=x1; (3) Если (x1>x2) и (f(x1)<f(x2)) a=x2; (4) Если (x1>x2) и (f(x1)>=f(x2)) b=x1; Увеличить счётчик числа итераций k=k+1 Шаг 2. Проверить критерий окончания поиска: если |ak+1-bk+1|£e - остановиться – минимум найден. Точнее фиксируем аппроксимирующий минимум как
double zoloto2(double a,double b) { double tau1,tau2,eps=0.0001,x1,x2; tau1 = (sqrt(5.0) - 1) / 2; // золотые числа tau2 = pow(tau1,2); x1=a+tau1*(abs(b-a)); x2=a+b-x1;
while (abs(b-a)>eps) { if ((x1<x2) && (f(x1)<f(x2))) b=x2; if ((x1<x2) && (f(x1)>=f(x2))) { a=x1; x1=x2; } if ((x1>x2) && (f(x1)<f(x2))) a=x2; if ((x1>x2) && (f(x1)>=f(x2))) { b=x1; x1=x2; } x2=a+b-x1; } return (x1); }
Метод Фибоначчи
Метод Фибоначчи является процедурой линейного поиска минимума унимодальной функции f(x) на замкнутом интервале [a, b], отличающейся от процедуры золотого сечения тем, что очередная пробная точка делит интервал локализации в отношении двух последовательных чисел Фибоначчи. Последовательность чисел Фибоначчи задаётся условиями F0 = F1 = 1, Fk+1 = Fk + Fk-1, k = 1,2,... Начальными членами последовательности будут 1, 1, 2, 3, 5, 8, 13,... Стратегия поиска Фибоначчи требует заранее указать n - число вычислений минимизируемой функции и e - константу различимости двух значений f(x). Рассмотрим один из возможных вариантов метода.
int Fib(int n) // n-ое число Фибоначчи { if (n > 1) return Fib(n-1)+Fib(n-2); else return 1; } Алгоритм Фибоначчи-1
Начальный этап (1) Задать константу e, начальный интервал [a1, b1], длину конечного интервала Ln и определить число n так, чтобы выполнялось условие Fn > (b1 - a1)/Ln. (2) Взять две пробные точки l1 = a1 + (Fn-2/Fn)(b1 - a1) и m1 = a1 + (Fn-1/Fn)(b1-a1). Положить k = 1. Основной этап Шаг 1. Сократить текущий интервал локализации: (1) Если f(lk) < f(mk), то положить ak+1 = ak, bk+1 = mk,mk+1 =lk и вычислить новую точку lk+1 = ak+1 + (Fn-k-2/Fn-k)Lk+1, где Lk+1 = bk+1 - ak+1; перейти на шаг 2. (2) Если f(lk)>> f(mk),то положить ak+1 =lk, bk+1 = bk, lk+1 = mk и вычислить mk+1 = ak+1 + (Fn-k-1/Fn-k) Lk+1. Шаг 2. Проверить критерий окончания поиска: (1) Заменить k на k+1. (2) Если k = n - 1, перейти на шаг 3, иначе - на шаг 1. Шаг 3. Найти аппроксимирующий минимум х(*): (1) Положить mk = lk + e. (2) Если f(lk) > f(mk), то x(*) = (lk + bk)/2. В противном случае - x(*) = (ak + mk)/2.
double Fibonacci(double a, double b, int &kFib) // Fibonacci - 1 { double lyambda, mu, eps = 0.0001, Ln = eps * 0.01; int n = 0; while (Fib(n) < (b - a) / Ln) // вычисление числа n n++; lyambda = a + (Fib(n - 2)*(b - a)) / Fib(n); // начальные точки mu = a + (Fib(n - 1)*(b - a)) / Fib(n); while (kFib < n - 1) // КОП: k = n - 1 { if (f(lyambda) < f(mu)) // определение направления сокращения { b = mu; // сокращение интервала mu = lyambda; lyambda = a + (Fib(n - kFib - 2)*(b - a)) / Fib(n - kFib); } else { a = lyambda; lyambda = mu; mu = a + (Fib(n - kFib - 1)*(b - a)) / Fib(n - kFib); } kFib++; } if (f(lyambda) > f(mu)) // определение конечного интервала return (lyambda + b) / 2; // середина интервала - аппроксимирующий минимум else return (a + mu) / 2; } Алгоритм Фибоначчи-2
Начальный этап (1) Задать константу e, начальный интервал [a1, b1], длину конечного интервала Ln и определить число n так, чтобы выполнялось условие Fn > (b1 - a1)/Ln. (2) Выбрать одну пробную точку k = 1. Основной этап Шаг 1. Проверить критерий окончания поиска: если k=n, то остановиться и положить x*=x2. Шаг 2. Сократить текущий интервал локализации рассмотрением 4-х ситуаций, аналогично методу золотого сечения-2.
double fibonachchi2(double a,double b,int n) { double x1,x2,eps=0.0001; x1=a+(Fib(n-1)/Fib(n))*(abs(a-b));//+ (pow(-1,n))*eps/Fib(n); int k = 1; x2=a+b-x1;
while (k!=n) { if ((x1<x2) && (f(x1)<f(x2))) b=x2; if ((x1<x2) && (f(x1)>=f(x2))) { a=x1; x1=x2; } if ((x1>x2) && (f(x1)<f(x2))) a=x2; if ((x1>x2) && (f(x1)>=f(x2))) { b=x1; x1=x2; } x2=a+b-x1; k++; } return x1; } С плавающими координатами double Bolzano(double a, double b) { double x1, a0, eps = 0.001; a0 = a; // расстояние от настоящего 0 до минимума b = b - a; a = 0; // смещение начала координат x1 = (a + b) / 2; while ((abs(proiz_f(x1))>eps) && (abs(b - a)>eps)) // КОП { if (proiz_f(x1) > 0) b = x1; // (b = x1 - a0)??? else { a0 = a0 + x1; b = b - x1; } x1 = (a + b) / 2; } x1 = x1 + a0; // вычисление координаты минимума от настоящего нуля return (x1); } Метод Пауэлла Метод Пауэлла является одним из самых популярных методов. Эффективен как и рассмотренный ранее алгоритм квадратичной интерполяции – экстраполяции, если начальная точка x1Îd(x*). Начальный этап 1. Выбрать ε1, ε2, h. 2. Взять 3 точки a, b, c на равных на равных интервалах. Предполагается, что сработал метод Свенна и получен интервал [a, b]. a=a; c=b; b=(a+c)/2; Основной этап 1. Найти аппроксимирующий минимум на 1-й итерации по формуле:
на последующих итерациях по формуле:
2. Проверить критерии близости двух точек:
Если он выполняется, принять Если не выполняется, то из 2-х точек b и d выбрать «лучшую» - в которой наименьшее значение функции, обозначить её как b, а 2 соседние с ней – a и c. Далее рассмотреть 4 ситуации аналогично ЗС-2. 3. Положить k=k+1 и вернуться на шаг 1. double Pauell(/*double alpha_a,double alpha_b*/) { double alpha_a,alpha_b, alpha_x; methodSwann(&alpha_a,&alpha_b); double alpha_c = alpha_b; alpha_b = (alpha_c + alpha_a)/2; double alpha_d=0.5*(f(alpha_a)*(alpha_b*alpha_b-alpha_c*alpha_c) + f(alpha_b)*(alpha_c*alpha_c-alpha_a*alpha_a) + f(alpha_c)*(alpha_a*alpha_a-alpha_b*alpha_b))/(f(alpha_a)*(alpha_b-alpha_c)+f(alpha_b)*(alpha_c-alpha_a)+f(alpha_c)*(alpha_a-alpha_b));
//while ((abs((alpha_b-alpha_d)/alpha_b)>eps) || (abs((f(alpha_b)-f(alpha_d))/f(alpha_b))>eps)) while (1) { if(f(alpha_b) >= f(alpha_d)) { if(alpha_b >= alpha_d) { alpha_c = alpha_b; }
else { alpha_a = alpha_b; } alpha_b = alpha_d; } else { if(alpha_b >= alpha_d) { alpha_a = alpha_d; } else { //alpha_b = alpha_d; alpha_c = alpha_d; }
} alpha_d = (alpha_a+alpha_b)/2 + 0.5 * (((f(alpha_a) - f(alpha_b))*(f(alpha_a) - f(alpha_b))*(alpha_b - alpha_c)*(alpha_c - alpha_a))/(f(alpha_a)*(alpha_b - alpha_c) + f(alpha_b)*(alpha_c - alpha_a) + f(alpha_c)*(alpha_a - alpha_b))); (k)++; if((fabs((alpha_b-alpha_d)/alpha_b) <= eps) || (fabs((f(alpha_b)-f(alpha_d)) / f(alpha_b)) <= eps)) break; if(k > 20) break; }
alpha_x = (alpha_b+alpha_d)/2; return alpha_x; }
Метод Давидона Начальный этап 1. Выбрать ε, x0, p, α1 2. Предполагается, что сработал метод Свенна и получен интервал [a, b]. Основной этап 1. Найти аппроксимирующий минимум, т.е. точку d по формулам:
2. Проверить КОП: если y`r≤ ε, то остановиться, х=a+αrp. Иначе: сократить ТИЛ: если y`r <0, то [r,b], если y`r >0, то [a,r]. Положить k=k+1 и вернуться на шаг 1.
double david(double a, double b) { double eps = 0.0001, gam, w, z, d, k = 0;
while (1) { z = df(a) + df(b) + (3 * (f(a) - f(b))) / (b - a); w = sqrt(z*z - df(a)*df(b)); gam = (z - df(a) + w) / ((df(b) - df(a) + 2 * w))*(b - a); d = a + gam; k++; //cout<<"\n---------DEVID NOW RUNNING k: "<<k<<"-------\n";
if (df(d) <= eps) { cout << "DAVID k: " << k << "\n"; cout << "DAVID gam: " << gam << "\n\n"; return (gam); } else { if (df(gam)<0) b = gam; else a = gam; } } } Метод Коши
Метод Коши относится к группе методов градиентного спуска. Градиентные методы – это методы, где на каждом шаге выбирается антиградиентное направление спуска. Начальный этап Выбрать x1, e, k. Основной этап Шаг 1
Шаг 2 (1) Найти L как результат минимизации функции по направлению p. (2) Шаг 3 (1) Вычислить новое значение градиента (2) Проверить КОП: если void KOSHI() { double eps = 0.0001, alfa; double xx1 = x0[0], xx2 = x0[1]; int k = 1;
//napr(); //swann(); //zs_2(a, b); //alfa=david(a, b);
//x1=x1+alfa*p1; //x2=x2+alfa*p2;
do { x0[0] = xx1; x0[1] = xx2; napr(); swann(); alfa = zs_2(a, b); //alfa=david(a, b);
xx1 = x0[0] + alfa*p1; xx2 = x0[1] + alfa*p2;
k++;
} while ((norm(xx1, xx2)>eps) || (fabs(f(0) - f(alfa))>eps)); }
Метод Гаусса-Зейделя Начальный этап Выбрать х1, ε = 10-4 – 10-8 установить k = 1; Основной этап: Шаг 1. Выполнить серию одномерных поисков вдоль координатных орт
Шаг 2. Вычислить ускоряющее направление и проверить КОП: Иначе: 1. Выполнить ускоряющий шаг в новую точку хn+2 2. Обозначить последнюю точку как начальную и вернуться на шаг 1.
Метод комплексов Бокса
Комплекс-метод предназначен для отыскания условного экстремума непрерывной целевой функции (1) в выпуклой допустимой области. При использовании метода принимаются следующие предположения: 1. Задача поиска экстремума функционала (1) решается при наличии ограничений 1-го и 2-го рода. 2. Значения целевой функции и функций ограничений могут быть вычислены в любой точке допустимой области изменения независимых переменных. 3. Допустимая область выпукла. 4. Значения целевой функции и функций ограничений вычисляются без ошибок. Идея комплекс метода заключается в последовательной замене точек некоторой конфигурации, удаленных от экстремума, на более близкие к нему. В отличие от симплексного метода, в комплексе-методе используется случайный набор N точек – Комплекс, а число точек Комплекса определяется по правилу:
  
где n – число независимых переменных. Вычислительная последовательность (алгоритм) комплекс-метода включает в себя следующие этапы. 1) Формируется исходный комплекс. Координаты вершин исходного Комплекса хij вычисляются последовательно с помощью равномерно распределенных на интервале (0;1) псевдослучайных чисел rij:
В каждой вершине с номером j проверяется выполнение ограничений 2-го рода (ограничения 1-го рода выполняются автоматически). Точка фиксируется как вершина Комплекса, если в ней удовлетворяются все ограничения. Если же ни в одной из точек ограничения не выполнены, то формуле (6) вычисляются координаты новых точек, в которых вновь проверяется ограничения. Пусть число точек, удовлетворяющих ограничениям 2-го рода Р (Р≥1), тогда (N–P) – число точек, в которых ограничения нарушены. Далее для каждой из еще незафиксированных вершин выполняется операция по ее смещению к центру Р вершин Комплекса, при этом новые координаты точки х*ij вычисляются по формуле
 , i=1, 2,…, n, j=P+1, P+2,…,N. , i=1, 2,…, n, j=P+1, P+2,…,N.
Процесс смещения j -й точки продолжается до тех пор, пока для нее не будут выполнены все ограничения. Такой момент обязательно наступит, поскольку допустимая область выпукла. Точка фиксируется как новая вершина Комплекса (Р увеличивается на единицу), после чего операция смещения повторяется для очередной вершины.
Fj=F(xj),
R=FG; S=FD. где G – номер самой «хорошей»; а D – самой «плохой» вершины. 4) Определяются координаты Ci центра Комплекса с отброшенной «наихудшей» вершиной:
 , i=1, 2,…,n. , i=1, 2,…,n.
5) Проверяется условие окончания поиска. Для этого вычисляется величина В:
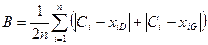 . .
Если В<ε (ε – заданная точность вычисления), т.е. среднее расстояние от центра Комплекса до худшей (D) и лучшей (G) вершин меньше ε, то поиск заканчивают, считая экстремум найденным. В противном случае вычисления продолжаются:
xi0=2,3Ci – 1,3xiD, i=1, 2,…,n. В этой новой точке проверяется выполнение ограничений 1-го рода. В случае, если ограничения нарушаются, xi0 принимает значения gi+ε или hi–ε в зависимости от того, в какую сторону i-е ограничение нарушено;
Процесс смещения продолжают до тех пор, пока все ограничения 2-го рода не будут соблюдены. 8) В новой точке вычисляют значения целевой функции F0:
  . .
Затем вновь вычисляют значение целевой функции F0 и сравнивают его с S. Смещением к лучшей вершине по формуле (15) продолжают до тех пор, пока F0 не станет лучше S. За счет этой процедуры происходит последовательное сжатие комплекса к лучшей вершине. 10) Если вычисленное в новой точке х0 значение F0 лучше S, то в Комплексе на месте наихудшей точки хD фиксируется точка х0 и значение S заменяется на F0. Затем вычисления повторяются, начиная с п. 3, и продолжаются до тех пор пока не будет выполнено условие остановки, т.е. не будет найден с заданной точностью экстремум целевой функции. Метод Ньютона
Если f(x) является дважды дифференцируемой в Rn, то эффективность процесса поиска точки х* ее минимума можно повысить, используя информацию не только о градиенте этой функции, но и о ее матрице Гecce H(x). Алгоритмы такого поиска обычно относят к методу Ньютона. В простейшем варианте алгоритма на каждой k-й итерации целевая функция аппроксимируется в окрестности точки xk-1 (на первой итерации в окрестности начальной точки х0) квадратичной функцией
Начальный этап: Выбрать x0, e, k=1. Основной этап Шаг 1 (1) Строится Ньютоновское направление: (2) Найти (3) (4) Шаг 3 Проверить КОП: если Метод Зангвилла Начальный этап Выбрать константу остановки Основной этап Шаг 1. Взять в качестве Шаг 2. Положить Шаг 3. Если Шаг 4. Положить
Флетчера-Ривса Метод сопряжённых направлений основан на свойствах векторов сопряженных относительно некоторой квадратной матрицы. Различие в способах построения системы сопряженных векторов, определяющих сопряжённые направления спуска, порождает несколько алгоритмов этого метода. В качестве матрицы сопряжений берётся матрица Гессе. Особенность алгоритмов метода сопряженных направлений состоит в том, что систему сопряженных векторов строят последовательно в процессе выполнения итераций, причем найденный на очередной, k-й итерации вектор pk определяет на этой итерации направление спуска. Для не квадратичных функций получаемые направления, в конце концов, перестают быть взаимносопряженными поэтому, как и в ДФП через n шагов вектор направления делают равным антиградиенту. Начальный этап Выбрать x1, e, k=1. Основной этап Шаг 1. Построить вектор pk:
Шаг 2. Найти новую точку Шаг 3. Проверить КОП:
Расчетное соотношение Флетчера-Ривса
Метод Пауэлла
Метод достаточно прост в реализации и обладает квадратичной сходимостью вблизи минимума. Стратегия метода базируется на свойстве квадратичных функций параллельного подпространства: если x1 минимум квадратичной функции по вектору p, а x2 минимум этой же функции по вектору параллельному предыдущему, то Первый вариант алгоритма метода Пауэлла Начальный этап (1) Выбрать x1, e, k=1. (2) Положить Основной этап: Шаг 1. (1) Выполнить n переходов по векторам базиса (2) Определить новое направление и спуститься вдоль него:
Шаг 2. Проверить КОП: если Шаг 3. Построить новую поисковую систему: из предыдущей системы удаляется первый вектор, а в конец добавляется вектор d. Таким образом изменение системы поиска выглядит так:
Второй вариант алгоритма метода Пауэлла Отличается от первого варианта тем, что изначально строится поисковая система где первый и последний вектор параллельны:
Изменение поисковой системы выглядит так:
double dichot(double a,double b) { double alpha,myu,eps=0.0001,del=0.1*eps; alpha=(a+b-del)/2; myu=(a+b+del)/2; while (abs(b-a)>eps) { if (f(alpha)<f(myu)) b=myu; else a=alpha; alpha=(a+b-del)/2; myu=(a+b+del)/2; } return ((a+b)/2); }
void main() { setlocale(0,"RUS");
double x2,x1=0,a,b,eps=0.0001,h; if (x1!=0) h=0.01*x1; else h=0.01; b=swanna(h,x1,x2); a=b-h; cout<<"f(x)= -exp(-x)*log(x)"<<endl; cout<<"Метод Свенна: a="<<a<<",b="<<b<<endl; //Метод Больцано x1=bolzan(a,b); cout<<"Метод Больцано: x="<<x1<<endl; //Метод дихотомии x1=dichot(a,b); cout<<"Метод Дихотомии: x="<<x1<<endl; //Метод золотого сечения 1 x1=zoloto(a,b); cout<<"Метод Золотого сечения 1: x="<<x1<<endl; //Метод золотого сечения 2 x1=zoloto2(a,b); cout<<"Метод Золотого сечения 2: x="<<x1<<endl; int n=0; while (Fib(n) < (abs(a-b)/eps)) n++; x1=fibonachchi1(a,b,n); cout<<"Метод Фибоначчи1: x="<<x1<<endl; x1=fibonachchi2(a,b,n); cout<<"Метод Фибоначчи2: x="<<x1<<endl; system("pause"); } МетодЫ решения оптимизационной задачи Курсовая работа включает в себя подавляющее большинство методов оптимизации, прочитанных в курсах «Методы оптимизации» и «Теория принятия решений». Каждый метод представлен в виде отдельной функции-члена класса. Все однотипные методы (в плане необходимых сведений для поиска) имеют одинаковое число аргументов. В большинстве своём - это начальная точка, погрешность максимальное количество шагов. В этом разделе представлены краткие описание методов оптимизации и применяемых математических формул. Сначала идут описания одномерных методов поиска, а затем многомерных.
  ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования...  ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры...  Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор...  ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|