Побудова мінімальних перевіряючих тестів (МПТ) та

Мінімальних тестів пошуку несправностей (МТПН)

Побудова мінімальних перевіряючих тестів (МПТ)

Мінімальний перевіряючий тест будується в два етапа:

1. будується усічена ТФН, в яку входять тільки рядки, які відповідають перевіркам вихідних елементів;

2. в МПТ включається мінімальна кількість перевірок вихідних елементів ОД, рядки яких спільно покривають нулями всі стовпчики несправних станів ОД.

В прикладі, що розглядається вихідними є елементи 4 і 5.

Усічена ТФН для них має такий вигляд (таблиця 2.2):

Таблиця 1.2

Перевірка π₅ покриває нулями всі стовпці несправних станів ОД, тому в МПТ входить тільки ця перевірка.

Це означає, що для визначення справного чи несправного стану ОД достатньо виконати тільки одну перевірку π₅.

Побудова мінімального тесту пошуку несправностей (МТПН)

Побудова мінімального тесту пошуку несправностей (МТПН) будується в чотири етапи:

1. визначення множини обов’язкових перевірок;

2. побудова усіченої ТФН для множини обов’язкових перевірок;

3. побудова таблиці перекриттів;

4. визначення множини додаткових перевірок.

1. Визначення множини обов’язкових перевірок.

В склад обов’язкових перевірок включаються:

– Перевірки вихідних елементів, які увійшли в МПТ;

– Перевірки інших елементів, які визначаються наступним чином. Якщо в ЛМ ОД є два елементи i та j та вихід елемента i з’єднаний тільки з входом елемента j, то перевірка π_і включається в число обов’язкових, в протилежному випадку перевірка π_і в число обов’язкових не включається.

Для прикладу, що розглядається в МПТ включається перевірка тільки одного вихідного елемента, перевірка π₅, яка повинна бути включена в множину обов’язкових перевірок Поб.

З перевірок елементів ОД які не є вихідними, в число обов’язкових включаються перевірки π_1,2 та π₃, так як вихід елемента 1₂ з’єднаний тільки з входом елемента 3, а вихід елемента 3 – тільки з входом елемента 5. Перевірки елементів 1₁ та 2 не включаються в число обов’язкових, тому що виходи цих елементів з’єднані з входами двох елементів. Таким чином,

.

2. Побудова усіченої ТФН.

Наступним етапом побудови МТПН є побудова усіченої ТФН, в яку включаються тільки рядки обов’язкових перевірок (табл. 2.3)

Таблиця 1.3

З аналізу таблиці 2.3 випливає, що в усіченій ТФН для множини Поб існують дві пари нерозрізнених стани:

3.1 Побудова таблиці покриттів.

Для розрізнення пар нерозрізнених станів будується таблиця покриттів і визначається множина додаткових перевірок Пдод.

Таблиця покриттів це прямокутна матриця (див. табл. 2.4), число стовпців якої дорівнює числу пар нерозрізнених станів, а число рядків дорівнює числу перевірок які не увійшли в число обов’язкових. В клітинах таблиці записується символ 1, якщо перевірки π_і розрізнюють стани, які увійшли в ту чи іншу пару станів, і символ 0 – в протилежному випадку.

Таблиця 1.4

3.2 Визначення множини додаткових перевірок.

В множину додаткових включається мінімальна сукупність перевірок елементів, які не увійшли в число обов’язкових і які спільно покривають одиницями всі стовпці таблиці покриттів.

Для прикладу, що розглядається можливі дві додаткові перевірки:

Якщо в усіченій ТФН є декілька однакових стовпців несправних станів s_і, s_j та s_k то стовпці таблиці покриттів позначуються всіма можливими сполученнями пар станів, тобто парами станів .

4 Визначення МТПН.

Мінімальний тест пошуку несправностей визначається шляхом об’єднання множини обов’язкових і додаткових перевірок МТПН П_об і П_дод. Для прикладу, що розглядається, можливі дві множини додаткових перевірок, тому існують два МТПН:

Побудова раціональних умовних алгоритмів

Пошуку несправностей

При умовних алгоритмах пошуку несправностей (АПН) вибір кожної наступної перевірки виконується із врахуванням результату попередньої перевірки. Найбільш зручною і наочною формою представлення умовних АПН є направлений граф, вершини якого відповідають станам процесу пошуку несправностей, а дуги показують, в якому стані в залежності від результатів перевірок здійснюється перехід на даному кроці процесу пошуку.

Для одного ОД існує багато умовних АПН, серед яких існує оптимальний, який забезпечує в середньому мінімальний час пошуку несправностей. Однак для побудови оптимального умовного АПН необхідний перебір великої кількості можливих АПН. Тому на практиці використовуються так звані раціональні умовні алгоритми АПН, які дозволяють отримати результати, що близькі до оптимальних. Раціональні умовні алгоритми пошуку несправностей (РУАПН) засновані на правилі (критерії), за допомогою якого вибирається наступна перевірка на кожному кроці процесу пошуку несправностей.

Критерії вибору перевірок, що використовуються в РУАПН можуть бути різними в залежності від особливостей ОД чи від повноти інформації об ОД. Звичайно вважається, що при побудові РУАПН існує наступна інформація об ОД:

- логічна модель чи ТФН ОД;

- множина перевірок П={ π_і }, що є тестом пошуку несправностей ОД

(не обов’язково мінімальним);

- множина Т={ t_і } значення затрат часу на виконування кожної з перевірок π_іÎП;

- множина Q ={ q_і }значень ймовірностей несправних станів елементів ОД.

В якості критеріїв вибору перевірок РУАПН використовуються наступні критерії:

1. Якщо відомі значення ймовірностей несправних станів елементів ОД, використовується критерій:

(1)

де: - множина станів ОД в яких він може знаходитися при негативному результаті перевірки p_і;

- множина станів ОД, в яких він може знаходитися при позитивному результаті перевірки p_і.

Цей критерій забезпечує побудову РУАПН в середньому за мінімальну кількість кроків (перевірок).

Для того щоб забезпечити мінімальний середній час відшукання несправності використовуємо критерій виду:

(2)

де t_і – середня тривалість перевірки p_і.

Якщо припустити, що ймовірності несправних станів елементів ОД однакові чи інформація про ці ймовірності відсутня, можна використати критерій:

(3)

чи

(4)

де - кількість станів, в яких може знаходитися ОД при негативному результаті перевірки p_і;

- кількість станів, в яких може знаходитися об’єкт при позитивному результаті перевірки p_і.

3. Приклад побудови раціонального умовного алгоритму

Пошуку несправностей

Нехай для прикладу, що розглядається вище дані наступні значення ймовірностей несправних станів: q₁=0.4, q₂=0.15, q₃=0.1, q₄=0.2, q₅=0.15, а також наступні значення затрат часу на виконання перевірок елементів ОД: t₁=20 хв, t₂=30 хв, t₃=40 хв, t₄=50 хв, t₅=60 хв.

У якості тесту пошуку несправностей виберемо раніше отриманий

, з якого виключимо перевірку p₅, так як думаємо, що пошук несправності буде здійснюватися тільки після перевірки справності (чи перевірки працездатності) ОД.

РУАПН будується в наступній послідовності:

1. Побудувати усічену ТФН для множини перевірок, що є тестом пошуку несправностей. В якості такого тесту вибираємо тест та будуємо усічену ТФН (див. табл. 3.1), в яку не включаємо стовпець справного стану ОД.

Таблиця 3.1

2. Побудуємо таблицю розрахунку РУАПН (див. табл. 3.2), в першому стовпці якої записуємо множину всіх несправних станів ОД.

3. Використовуя ЗТФН (табл. 3.1) визначити множину перевірок, придатних до множини S.

Придатними до множини S називаються перевірки π_і, які виділяють на множині S непусті підмножини та , де - множина станів, в якому знаходиться ОД при негативному, а - при позитивному результаті перевірки π_і.

Наприклад, перевіркою π_1,2 на множині виділяються підмножини та .

Всі придатні перевірки записують в стовпці 2 таблиці 3.1, а підмножини в стовпцях 3 і 4.

4. Для кожної з перевірок розрахувати значення критерію , у відповідності з одним з виразів (1), (2), (3) чи (4) та записати в стовпці 5. Якщо придатна перевірка – одна, то значення критерію не розраховуються, а перевірка приймається в якості оптимальної і записується в стовпці 6.

Вважаємо що і розрахуємо значення за формулою:

.

Для перевірки π_1,2 отримаємо:

.

Для перевірки π₂ маємо:

Для перевірки π₃ отримаємо:

Таблиця 3.2

Множина (підмножина) станів ОД.	Придатні перевірки πі	Виділені підмножини
				-
				-

В якості оптимальної вибирається перевірка, для якої значення розрахованого критерію мінімально. Такою перевіркою є перевірка , тому що =0. Символ перевірки записується в стовпчик 6 таб. 3.2.

5. Відповідні оптимальній перевірці виділенні нею підмножини та , які мають два та більше елементів, записують одне під одним в стовпчику 1 таб. 3.2, тобто підмножини =S та =S.

6. Якщо в стовпчику 1 табл. 3.2 є підмножини, для яких оптимальні перевірки не визначені, прийняти цю підмножину в якості множини S і для кожної з цих підмножин виконати п.п. 3...5 даного алгоритму. В противному випадку перейти до виконання наступного пункту.

Виконаємо п.п. 3...5 алгоритму для підмножини

Для цієї підмножини по ЗТФН (таб.3.1) визначимо придатні перевірки та , які записуються в стовпчику2 табл. 3.2, а виділені цими перевірками підмножини відповідно та для та і для перевірки , записуємо в стовпчиках 3 і 4 табл.3.2.

Розрахуємо значення критерію для цих перевірок:

Для перевірки :

Для перевірки :

В якості оптимальної вибираємо перевірку , так як Ця перевірка виділяє на множині підмножину, яка має один елемент і підмножину, яка має два елемента . Ця підмножина записується в стовпчику 1 табл. 3.2 (після раніше виділеного перевіркою підмножини ). Підмножина в таблицю не записується, так як воно включає тільки один елемент.

Використання для підмножин та пунктів 3...5 алгоритму дає наступні результати.

У відповідності з п.3 алгоритму визначаємо придатні перевірки для цих підмножин. Для кожної з зазначених підмножин існує єдина придатна перевірка . У зв’язку з тим, що зазначена перевірка в обох випадках являється єдиною, розрахунок значення критерію вибору перевірок не проводиться, і перевірка двічі обирається в якості оптимальної.

В результаті виконання перевірки для розрізнення станів множин і отримані одноелементні підмножини і , в стовпчику 1 таблиці 3.2. ніяких нових множин не записано, тому виконується п.7 алгоритму.

7. Побудувати граф отриманого РУАПН, який має вигляд, приведений на рисунку 3.

Аналогічним чином виконується побудова РУАПН, якщо для розрахунку критерію вибору перевірок використовуються формули (2), (3) і (4).

Рисунок 3

4. Вироджене покриття

Одержимо вироджене покриття і d-куби, наприклад логічної функції трьох аргументів .

Перевести десяткове число 206 в двійкову систему числення:

.

Навести таблицю істинності функції в наступному вигляді:

Таблиця 4.1

а в с

Одержати мінімальну диз’юктивну нормальну форму заданої функції та її інверсії .

Використовуючи діаграму Дейча маємо:

Рисунок 4. Діаграми Дейча функцій і .

Записати одиничні та нульові куби виродженого покриття, виходячі з мінімальної ДНФ функцій і :

Таблиця 4.2

Аргументи функції а в с	Значення функції	Куби
1 х 0 0 0 х		Одиничні куби
1 х 1 0 1 х		Нульові куби

Одержати d-куби функції шляхом порозрядного перетину одиничних та нульових кубів виродженого покриття:

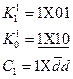
Привести умовне графічне позначення логічного елемента, який реалізує функцію , виходячи з мінімальної ДНФ:

Рисунок 5. Функціональна схема та умовне графічне

позначення елемента

5. Визначення вхідного набору

1. Вивчити сутність операції просування вектору стану схеми ДП до входів і виходів [1], стор.32-36.

2. Вивчити алгоритм визначення вхідного тестового набору, який виявляє задану несправність [1], підрозділ 4.2.

3. Розв’язати задачу 5 згідно заданому варіанту.

4. Розглянемо методику розв’язання задачі 5 на прикладі схеми дискретного пристрою, наведеної на наступному рисунку.

Рисунок 6. Функціональна схема дискретного пристрою

Послідовність розв’язування задачі наступна:

1. Виконати ранжування елементів схеми, тобто пронумерувати елементи схеми наступним чином:

- входам ДП присвоїти молодші номери 1, 2 і 3 (цифри в дужках на рисунку), а виходам логічних елементів (ЛЕ) присвоїти наступні номери – 4, 5,...,9.

2. Визначити d-куб заданої несправності , тобто константа 1 на виході четвертого елемента. З цією метою визначити вхідний набір елемента, який виявляє задану несправність. Кращім з наборів елемента 2И 00, 01, 10 є набір 00.

Виконати перетин цього набору при умові, що несправність має місце з тестовим набором справного елементу. Одержимо наступний d-куб заданої несправності:

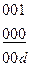
3. Побудувати таблицю для визначення тестового набору (таблиця 5.1). Записати в таблицю d-покриття схеми, яке являє собою сукупність d-кубів елементів схеми (рядки 1...13 таблиці).

Таблиця 5.1

№ рядка

Входи ДП

Логічні елементи

Позна-чення

Пояснення

Актив-ність

d-розгалу-ження

d

d

d

d

d

d

d

d

d

d

d

d

d – куби

d

d

елементів 4...9

d

d

d

d

d

d

d

d

d

d

d

d

C

d

C

C

C

C

C

d-куб несправності

{4}

{6,7}

C

C

d

C

d

C

C

C

C

m

C

d

C

C

C

C

d

C

C

C

C

{4,6}

{8,9}

C

C

C

d

C

C

C

C

Y

C

C

C

d

C

d

C

C

C

C

l

C

C

C

C

d

C

C

C

C

Y

C

C

C

C

d

C

d

C

C

C

Y

C

C

C

C

d

C

d

C

C

C

m

C

d

C

C

C

d

C

d

C

C

{4,7}

{9}

C

d

C

d

C

C

C

{4,6}

{8,9}

C

C

C

C

C

d

C

d

C

C

d

C

l

C

d

C

C

C

C

C

C

d

C

d

C

C

d

C

m

C

d

C

C

d

C

d

C

d

C

{4,6,8}

{Æ}, вихід

C

C

C

C

C

d

C

d

C

d

C

Y

d

d

C

C

C

C

C

d

C

d

C

d

C

m

C

d

C

d

C

d

C

d

{4,6,9}

{Æ}, вихід

C

d

C

d

C

C

{4,7}

{9}

C

C

C

C

C

d

C

d

C

d

m

C

d

C

d

d

C

d

{4,7,9}

{Æ}, вихід

C

C

C

C

C

d

C

d

C

d

d

Y

C

d

4. В стовпці „Входи ДП” і „Логічні елементи” таблиці записати початковий вектор стану схеми , в якості якого взятий d-куб заданої несправності, а в стовпці „активність” „d-розгалуження” – відповідно номери елементів, які входять в активізовані шляхи транспортування несправності на виході схеми, і номери елементів, через які несправність може транспортуватися на виходи схеми.

Активізовані шляхи починаються з несправного елемента, тому в стовпець „ Активність” записується 4, а в стовпець „d-розгалуження”- номери елементів 6 і 7 (рядок 14 таблиці).

5. Здійснити спробу просування заданої несправності на виходи схеми через елементи, які входять в d-розгалуження. Для цього виконати перетин поточного вектора стану схеми з усіма d-кубами елементів d-розгалуження.

В результаті перетину вектора з d-кубами ... елемента 6 одержуються відповідно вектори (рядок 17 таблиці), і (рядок 19 таблиці), (рядок 21 таблиці) і (рядок 23 таблиці).

Перетин 4-х розрядів вектора і куба дає символ m (рядок 16 таблиці), який замінюється символом d (рядок 17 таблиці), а перетин 2-х і 4-х розрядів вектора і куба дає символ Y (рядок 19 таблиці), що означає невизначеність. Тому вектор в подальшому не розглядається, а для вектора

Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...

Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...

Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все...

ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала...

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: