|
|
Сила избыточного суммарного давления жидкости на плоскую фигуру равна произведению площади фигуры S на избыточное давление в ее центре тяжести.Стр 1 из 6Следующая ⇒ Это правило остается справедливым и для полного суммарного давления, т.е. при учете давления на свободной поверхности жидкости р0. В этом случае
Центр давления. Точка, в которой приложена равнодействующая гидростатического давления жидкости на плоскую площадку, называется центром давления. Расстояние вдоль стенки от свободной поверхности до центра давления lц.д. равно lц.д.=lц.т.+ где I0 – момент инерции рассматриваемой фигуры относительно оси, проходящей через ее центр тяжести. Последняя формула показывает, что центр давления расположен ниже центра тяжести. Для вертикальной, прямоугольной плоской стенки высотой h и шириной b (глубина воды h) hц.т.=
Решение. Силу F избыточного давления определяем по формуле (7.12), площадь на которую действует давление, равна F=1000 ∙ 9,8 ∙ 0,75 ∙ 15=110250 Н.
Задача 7.8. Определить силу F, необходимую для подъема щита С, закрывающего прямоугольное отверстие высотой h=3 м и шириной В=4 м (рис. 7.13). Напор воды перед щитом H=5 м, коэффициент трения в направляющих щита при подъеме f=0,03, вес щита 500 кг.
Давление жидкости на криволинейные поверхности Представим цилиндрическую криволинейную поверхность АВ, на которую слева действует жидкость (рис. 7.14). В данном случае нахождение
При решении данной задачи достаточно определить отдельные проекции суммарной силы. Не приводя доказательств, сформулируем результат вывода формулы для величин горизонтальных составляющих суммарной силы: горизонтальная составляющая суммарного давления на криволинейную поверхность равна силе суммарного давления на ее вертикальную проекцию. Если определяется проекция силы давления на ось Х, то поверхность АВ (единичной ширины) проектируется на плоскость YОZ (вертикальная плоскость ВВ´ на рис. 7.14); в результате получаем Fx= Таким образом, чтобы найти горизонтальную составляющую силы давления, надо криволинейную поверхность спроектировать на вертикальную плоскость и определить силу давления на нее, как на плоскую стенку. Переходя к вертикальной составляющей силы суммарного давления, введем представление о теле давления: объем W называется телом давления (рис. 7.14); он ограничен криволинейной поверхностью АВ, проекцией ее на плоскость свободной поверхности АВ´ и вертикальной плоскостью проектирования ВВ´.
Fz= Задача 7.9. Металлическая цистерна диаметром D=2,4 м и длиной l=12 м заполнена нефтью (плотность нефти Решение. Горизонтальную составляющую определим по формуле (7.15) Fx= (составляющая Fy равна нулю). Вертикальную составляющую находим с помощью зависимости (7.16) Fz= Равнодействующая равна Угол наклона равнодействующей к горизонту можно найти, подсчитав величину
Закон Архимеда
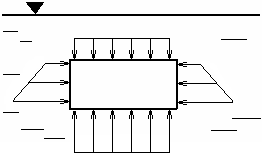 На погруженное в жидкость тело действуют поверхностные силы давления (рис. 7.16), значения которых соответствуют площадям эпюр гидростатического давления. Горизонтальные силы давления, действующие на боковые поверхности тела, взаимно уравновешиваются. Вертикальные силы давления равны весу жидкости в объемах соответствующих тел давления; равнодействующая вертикальных сил называется архимедовой силой и направлена вверх.
  Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? - задался я вопросом...  Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...  ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала...  Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|
(р0+ 
) S. (7.13)
,
, hц.д.= 
h. (7.14)
Задача 7.7. Подпорная вертикальная прямоугольная стенка шириной В=10 м сдерживает напор воды высотой Н=1,5 м. Определить силу избыточного давления F на стенку. Плотность воды принять 
=1000 кг/м3.
10 ∙ 1,5=15 м2. Так как стенка прямоугольная, то ее центр тяжести находится в точке пересечения диагоналей и глубина погружения его под поверхностью воды равна hц.т.= 0,75 м. Окончательно величина силы F равна
силы гидростатического давления, действующего на криволинейную стенку, осложняется тем, что необходимо суммировать силы, имеющие различные направления (ясно, что в каждой точке давление направлено по 
. (7.16)
=850 кг/м3). Давление на поверхности нефти равно атмосферному (рис. 7.15). Определить силу давления нефти на левую внутреннюю криволинейную поверхность АВ.
ld 
= 
=850 ∙ 9,81 ∙ 12 ∙ 
=288178,5 H
= 850 ∙ 9,81 ∙ 12 ∙ 
=72044,6 Н.
=297047 Н.
.