|
Уравнение прямой, проходящей через заданную
Точку с заданным угловым коэффициентом. Уравнение прямой, проходящей через две заданные точки
Пусть дана точка 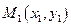 , лежащая на прямой, и известен угловой коэффициент , лежащая на прямой, и известен угловой коэффициент  этой прямой. Нужно записать ее уравнение. этой прямой. Нужно записать ее уравнение.
Так как эта прямая проходит через точку 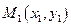 , то ее координаты удовлетворяют уравнению (30), т. е. , то ее координаты удовлетворяют уравнению (30), т. е.  . Полученное соотношение вычтем из (30) и придем к уравнению прямой, проходящей через точку . Полученное соотношение вычтем из (30) и придем к уравнению прямой, проходящей через точку 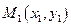 : :
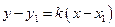 . (31) . (31)
Пусть теперь даны две точки 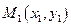 и и  . Нужно записать уравнение прямой, проходящей через них. Здесь можем воспользоваться уравнением (31). Величина . Нужно записать уравнение прямой, проходящей через них. Здесь можем воспользоваться уравнением (31). Величина  пока не известна. Учтём, что прямая проходит также через точку пока не известна. Учтём, что прямая проходит также через точку  , поэтому координаты этой точки должны удовлетворять уравнению (31), т. е. , поэтому координаты этой точки должны удовлетворять уравнению (31), т. е. 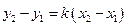 . Исключим . Исключим  из последних двух уравнений. Для этого нужно соотношение (31) почленно поделить на последнее. Получим искомое уравнение из последних двух уравнений. Для этого нужно соотношение (31) почленно поделить на последнее. Получим искомое уравнение 
Кривые второго порядка. Окружность
Кривой второго порядка называется линия на плоскости  определяемая уравнением второй степени относительно текущих координат определяемая уравнением второй степени относительно текущих координат  , ,  вида вида
 . (32) . (32)
Здесь  , ,  , ,  , ,  , ,  , ,  –заданные числа, называемые коэффициентами уравнения. Cчитаем, что в этом уравнении коэффициенты –заданные числа, называемые коэффициентами уравнения. Cчитаем, что в этом уравнении коэффициенты  , ,  , ,  одновременно не обращаются в нуль, поскольку в противном случае (32) обращается в уравнение первой степени. одновременно не обращаются в нуль, поскольку в противном случае (32) обращается в уравнение первой степени.
Рассмотрим отдельные случаи уравнения (32) и соответствующие им кривые.
Окружность. Как мы уже знаем, окружность радиуса  с центром в точке с центром в точке  имеет уравнение имеет уравнение
 . (33) . (33)
В уравнении (33) в левой части раскроем скобки и получим
 . (34) . (34)
В уравнении (34) коэффициенты при квадратах текущих координат равны друг другу. Кроме того, в этом уравнении отсутствует член, содержащий произведение текущих координат. Легко проверить, что если в уравнении (32)  , , 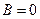 , то оно будет определять окружность в плоскости , то оно будет определять окружность в плоскости  (если уравнению отвечает множество точек). Чтобы убедиться в сказанном, достаточно уравнение (32) поделить на (если уравнению отвечает множество точек). Чтобы убедиться в сказанном, достаточно уравнение (32) поделить на  , после чего в левой части выделить полные квадраты членов, содержащих , после чего в левой части выделить полные квадраты членов, содержащих  , и полные квадраты членов, содержащих , и полные квадраты членов, содержащих  . Таким образом перейдём к уравнению вида (33): . Таким образом перейдём к уравнению вида (33):
 . .
Эллипс
 Эллипсом называется геометрическое место точек на плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная. Эту постоянную обозначим через Эллипсом называется геометрическое место точек на плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная. Эту постоянную обозначим через  , ,  , а фокусы – через , а фокусы – через  и и 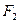 . Расстояние между ними . Расстояние между ними  . Ось Ox проведём через фокусы. Начало координат О возьмём в середине отрезка, соединяющего фокусы. При указанном выборе осей координаты фокусов . Ось Ox проведём через фокусы. Начало координат О возьмём в середине отрезка, соединяющего фокусы. При указанном выборе осей координаты фокусов  , ,  . Пусть . Пусть  – произвольная точка эллипса, соединим ее с – произвольная точка эллипса, соединим ее с  и и 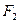 (рис. 24). По определению эллипса сумма расстояний от любой точки эллипса до фокусов равна (рис. 24). По определению эллипса сумма расстояний от любой точки эллипса до фокусов равна  , т. е. , т. е.
 . (35) . (35)
Из треугольника  видно, что видно, что  . Запишем расстояния через координаты: . Запишем расстояния через координаты:
 , ,  . (36) . (36)
Эти выражения подставим в (35) и получим
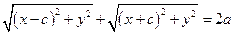 . .
Последнему соотношению удовлетворяют координаты любой точки эллипса, следовательно, это соотношение – уравнение эллипса. Нужно его упростить. Второй корень перенесём из левой части вправо и возведём обе части уравнения в квадрат. Тогда будем иметь
 , ,
 . .
После приведения подобных членов в правой части оставим корень с множителем, остальные слагаемые перенесём влево и полученное выражение возведём в квадрат. Обозначим  (так как (так как  ), считая ), считая  После простых преобразований получим соотношение После простых преобразований получим соотношение
 . (37) . (37)
Такое уравнение эллипса называется каноническим. Имея уравнение (37), выясним форму эллипса.
Пусть  – произвольная точка эллипса. На плоскости – произвольная точка эллипса. На плоскости  возьмём точку возьмём точку  , имеющую ту же абсциссу , имеющую ту же абсциссу  , что и точка М, а ординату , что и точка М, а ординату  , отличающуюся от ординаты точки М только знаком. Точка , отличающуюся от ординаты точки М только знаком. Точка  симметрична симметрична  относительно оси Ox. Уравнение (37) содержит относительно оси Ox. Уравнение (37) содержит  только во второй степени и только во второй степени и  . Точка . Точка  лежит на эллипсе, поэтому её координаты удовлетворяют уравнению эллипса, но тогда этому уравнению удовлетворяют координаты точки лежит на эллипсе, поэтому её координаты удовлетворяют уравнению эллипса, но тогда этому уравнению удовлетворяют координаты точки  , так как абсцисса точки М равна абсциссе , так как абсцисса точки М равна абсциссе  , а ординаты различаются лишь знаком. Получаем, что точка , а ординаты различаются лишь знаком. Получаем, что точка  лежит на эллипсе, но сказанное относится к произвольной точке лежит на эллипсе, но сказанное относится к произвольной точке  эллипса, следовательно, эллипс будет симметричным относительно оси Ox. Так как в (37) эллипса, следовательно, эллипс будет симметричным относительно оси Ox. Так как в (37)  содержится только в квадрате, рассуждая аналогично, покажем, что ось Oy также является осью симметрии эллипса, следовательно, начало координат содержится только в квадрате, рассуждая аналогично, покажем, что ось Oy также является осью симметрии эллипса, следовательно, начало координат  – центр симметрии эллипса. В силу симметрии форму эллипса достаточно выяснить для первой четверти плоскости – центр симметрии эллипса. В силу симметрии форму эллипса достаточно выяснить для первой четверти плоскости  для которой для которой  и и  . Для таких значений . Для таких значений  и и  уравнение (37) запишем так: уравнение (37) запишем так:
 . (38) . (38)
Получили выражение для ординаты  точки точки  эллипса с абсциссой эллипса с абсциссой  Когда абсцисса точки Когда абсцисса точки  принимает значение принимает значение  , то согласно (38) ее ордината , то согласно (38) ее ордината  . Точка . Точка  находится на Oy в точке находится на Oy в точке  . С увеличением абсциссы точки . С увеличением абсциссы точки  ордината этой точки согласно (38) уменьшается. Точка ордината этой точки согласно (38) уменьшается. Точка  опускается и при опускается и при  ордината этой точки будет равна нулю, ордината этой точки будет равна нулю,  совпадет с точкой совпадет с точкой  . Остальные части эллипса вычерчиваются по симметрии. Точки . Остальные части эллипса вычерчиваются по симметрии. Точки  называются вершинами эллипса, а числа называются вершинами эллипса, а числа  и и  – большой и малой осями эллипса соответственно (см. рис. 24). – большой и малой осями эллипса соответственно (см. рис. 24).
Гипербола
 Гиперболой называется геометрическое место точек плоскости, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (рис. 25). Обозначим эту постоянную Гиперболой называется геометрическое место точек плоскости, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (рис. 25). Обозначим эту постоянную  , а фокусы – через , а фокусы – через  и и 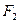 . Расстояние между ними . Расстояние между ними  . Ось Ox проведём через фокусы. Начало координат О возьмём в середине отрезка . Ось Ox проведём через фокусы. Начало координат О возьмём в середине отрезка  . Тогда фокусы имеют координаты . Тогда фокусы имеют координаты  , ,  . Пусть . Пусть  – произвольная точка гиперболы, тогда по определению – произвольная точка гиперболы, тогда по определению
  . (39) . (39)
Знак «+» берётся, когда левая часть положительна, а знак «-» – когда левая часть отрицательна. Расстояния 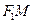 и и  , как и раньше, выражаются формулами (36). Подставим (36) в (39): , как и раньше, выражаются формулами (36). Подставим (36) в (39):
 . (40) . (40)
Получили уравнение гиперболы. Как видно из рис. 25,  есть длина стороны есть длина стороны  треугольника треугольника  , и она больше , и она больше  , поэтому , поэтому 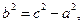  – действительное число, которое будем считать положительным. Уравнение (40) упростим, убрав корни так же, как в уравнении эллипса. Получим каноническое уравнение гиперболы – действительное число, которое будем считать положительным. Уравнение (40) упростим, убрав корни так же, как в уравнении эллипса. Получим каноническое уравнение гиперболы
 (41) (41)
Исследуем форму гиперболы, исходя из уравнения (41) (как и в случае эллипса). Так как (41) содержит  и и  только во второй степени, то Ox и Oy являются осями симметрии гиперболы (аналогично случаю эллипса), поэтому точка пересечения этих осей – начало координат только во второй степени, то Ox и Oy являются осями симметрии гиперболы (аналогично случаю эллипса), поэтому точка пересечения этих осей – начало координат  – центр симметрии гиперболы. Ясно, что для установления вида гиперболы достаточно рассмотреть картину в первой четверти плоскости, где – центр симметрии гиперболы. Ясно, что для установления вида гиперболы достаточно рассмотреть картину в первой четверти плоскости, где  и и  . Для таких значений . Для таких значений  , ,  из уравнения (41) выразим из уравнения (41) выразим  и получим и получим
 . (42) . (42)
Эта формула выражает ординату  точки точки  гиперболы, абсцисса которой есть гиперболы, абсцисса которой есть  . При . При  ордината ордината  , получим точку , получим точку  гиперболы. С увеличением абсциссы точки гиперболы. С увеличением абсциссы точки  её ордината согласно (42) увеличивается. Точка её ордината согласно (42) увеличивается. Точка  уходит вправо, неограниченно поднимаясь вверх. Остальные части гиперболы строятся по симметрии. уходит вправо, неограниченно поднимаясь вверх. Остальные части гиперболы строятся по симметрии.
Определим вид гиперболы, когда  неограниченно увеличивается. Возьмём прямую с уравнением неограниченно увеличивается. Возьмём прямую с уравнением
 (43) (43)
проходящую через точки  и и  Пусть Пусть  – точка прямой (43), имеющая ту же абсциссу x, что и точка M гиперболы. Ординаты этих точек равны – точка прямой (43), имеющая ту же абсциссу x, что и точка M гиперболы. Ординаты этих точек равны  и и  , так как координаты этих точек удовлетворяют (43) и уравнению гиперболы (42). Разность между указанными ординатами равна расстоянию между точками , так как координаты этих точек удовлетворяют (43) и уравнению гиперболы (42). Разность между указанными ординатами равна расстоянию между точками  и и  , следовательно, , следовательно,
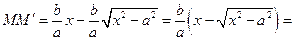
 . .
Для положительных  знаменатель с увеличением знаменатель с увеличением  неограниченно увеличивается, поэтому дробь убывает. Таким образом, неограниченно увеличивается, поэтому дробь убывает. Таким образом,  стремится к нулю, т. е. точка стремится к нулю, т. е. точка  гиперболы приближается к точке гиперболы приближается к точке  прямой. В силу симметрии относительно прямой. В силу симметрии относительно  такая же картина будет в третьей четверти плоскости. такая же картина будет в третьей четверти плоскости.
Возьмём теперь прямую
 . (44) . (44)
Она симметрична с прямой (43) относительно Ox, проходит через точку  и через точку и через точку  , симметричную с , симметричную с  относительно Ox. В силу симметрии гиперболы относительнооси абсцисс ясно, что гипербола по отношению к прямой (44) расположена аналогично её расположению к прямой (43). Прямые (43) и (44) называются асимптотами. относительно Ox. В силу симметрии гиперболы относительнооси абсцисс ясно, что гипербола по отношению к прямой (44) расположена аналогично её расположению к прямой (43). Прямые (43) и (44) называются асимптотами.
При построении гиперболы целесообразно сначала начертить ее асимптоты. Точки  и и  пересечения гиперболы с осью Ox называются вершинами гиперболы. Расстояние между ними равно пересечения гиперболы с осью Ox называются вершинами гиперболы. Расстояние между ними равно  , ,  называется действительной осью гиперболы; называется действительной осью гиперболы;  и называется мнимой осью. и называется мнимой осью.
Парабола
Параболой называется геометрическое место точек на плоскости, равноудалённых от заданной точки, называемой фокусом, и заданной прямой, называемой директрисой. Пусть  – фокус. Ось Ox проведём через – фокус. Ось Ox проведём через  перпендикулярно директрисе (рис. 26). перпендикулярно директрисе (рис. 26).
 Пусть Пусть  – расстояние от фокуса – расстояние от фокуса  до директрисы. Это число задано и называется параметром параболы. Начало координат возьмём в середине перпендикуляра, опущенного из точки до директрисы. Это число задано и называется параметром параболы. Начало координат возьмём в середине перпендикуляра, опущенного из точки  на директрису. Тогда фокус будет иметь координаты на директрису. Тогда фокус будет иметь координаты 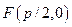 . Директриса имеет уравнение . Директриса имеет уравнение  . Пусть . Пусть  – произвольная точка параболы, – произвольная точка параболы,  – основание перпендикуляра, опущенного из точки – основание перпендикуляра, опущенного из точки  на директрису. Из рис. 26 видно, что расстояние на директрису. Из рис. 26 видно, что расстояние
 . (45) . (45)
Запишем расстояние от  до до  : :
 (46) (46)
Для любой точки  параболы имеем параболы имеем  (по определению). Подставим сюда выражения (45), (46) и получим уравнение параболы (по определению). Подставим сюда выражения (45), (46) и получим уравнение параболы
 . .
Упростим его, избавляясь от корня. Получим каноническое уравнение параболы
 . (47) . (47)
 Исследуем форму параболы по уравнению (47). Так как это уравнение содержит Исследуем форму параболы по уравнению (47). Так как это уравнение содержит  только во второй степени, то, как и в случае эллипса, Ox является осью симметрии параболы. Следовательно, вид параболы достаточно установить в верхней полуплоскости, где только во второй степени, то, как и в случае эллипса, Ox является осью симметрии параболы. Следовательно, вид параболы достаточно установить в верхней полуплоскости, где  . Для таких значений . Для таких значений  уравнение (47) запишем в виде уравнение (47) запишем в виде  . Эта формула выражает ординату точки . Эта формула выражает ординату точки  , абсцисса которой равна , абсцисса которой равна  . Когда . Когда  , согласно последней формуле , согласно последней формуле  , точка , точка  совпадает с совпадает с  . С увеличением . С увеличением  – абсциссы точки – абсциссы точки  – её ордината, равная – её ордината, равная  , неограниченно растёт, и точка , неограниченно растёт, и точка  уходит вверх и вправо. В силу симметрии остальная часть параболы вычерчивается сразу. Если Ox провести от уходит вверх и вправо. В силу симметрии остальная часть параболы вычерчивается сразу. Если Ox провести от  к директрисе, то получим параболу, изображенную на рис. 27. Легко проверить, что уравнение параболы в этом случае будет иметь вид к директрисе, то получим параболу, изображенную на рис. 27. Легко проверить, что уравнение параболы в этом случае будет иметь вид  Пусть теперь ось Oy направлена Пусть теперь ось Oy направлена  перпендикулярно к директрисе и проходит через перпендикулярно к директрисе и проходит через  . При этом уравнение параболы будет иметь вид . При этом уравнение параболы будет иметь вид  (см. рис. 28). (см. рис. 28).
§16. Преобразование координат на плоскости
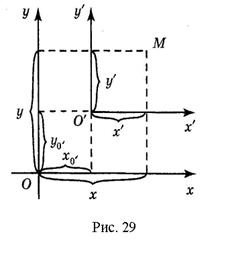
Параллельный перенос осей координат. Пусть  – исходная система координат, – исходная система координат, 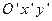 – новая система координат, полученная параллельным переносом исходной системы, как показано на рис. 29. Положение новой системы по отношению к старой определим, задав координаты – новая система координат, полученная параллельным переносом исходной системы, как показано на рис. 29. Положение новой системы по отношению к старой определим, задав координаты  нового начала нового начала  в старой системе координат, где в старой системе координат, где  – заданные числа. Пусть – заданные числа. Пусть  , ,  – координаты точки – координаты точки  в новой системе, в новой системе,  – координаты точки – координаты точки  в исходной системе. Как видно из рис. 29, в исходной системе. Как видно из рис. 29,  , , 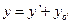 . Итак, . Итак,
 (48) (48)
Эти формулы выражают старые координаты 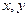 точки точки  через её новые координаты. через её новые координаты.
Поворот осей координат. Пусть  – исходная система координат, а новая система координат получена поворотом исходной вокруг начала координат на угол a, где a – заданное число (см. рис. 30). Угол – исходная система координат, а новая система координат получена поворотом исходной вокруг начала координат на угол a, где a – заданное число (см. рис. 30). Угол  берётся со знаком «+», если отсчёт ведётся против хода часовой стрелки от оси Ox. Пусть берётся со знаком «+», если отсчёт ведётся против хода часовой стрелки от оси Ox. Пусть 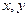 – координаты точки – координаты точки  в системе в системе  , ,  – координаты точки – координаты точки  в системе в системе 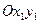 . Пусть . Пусть  и и  – угол, образованный отрезком – угол, образованный отрезком  с осью с осью  , причём, как и , причём, как и  этот угол берётся со знаком «+», если отсчёт ведётся от оси этот угол берётся со знаком «+», если отсчёт ведётся от оси  против хода часовой стрелки. Из рис. 30 видно, что против хода часовой стрелки. Из рис. 30 видно, что
 (49) (49)
С другой стороны,
 (50) (50)
Формулы (50) перепишем, использовав известные формулы тригонометрии для косинуса и синуса суммы:   С учётом (49) запишем С учётом (49) запишем
 (51) (51)
Эти формулы выражают старые координаты точки  через её новые координаты в случае поворота осей координат. через её новые координаты в случае поворота осей координат.
Общий случай. Пусть  – исходная система координат, – исходная система координат,  – новая система координат (рис. 31). Положение новой системы по отношению к старой определим, задав: – новая система координат (рис. 31). Положение новой системы по отношению к старой определим, задав:
· координаты  нового начала нового начала  в старой системе координат; в старой системе координат;
· угол  который образует ось который образует ось  с Ox. с Ox.
Пусть 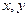 – координаты точки – координаты точки  в старой системе, а в старой системе, а  – координаты точки – координаты точки  в новой системе. Нужно найти связь между ними. С этой целью введём вспомогательную систему координат в новой системе. Нужно найти связь между ними. С этой целью введём вспомогательную систему координат  , полученную параллельным переносом старой системы , полученную параллельным переносом старой системы  Пусть Пусть  , ,  – координаты точки – координаты точки  в этой вспомогательной системе. Так как новая система координат в этой вспомогательной системе. Так как новая система координат  получена поворотом вспомогательной системы получена поворотом вспомогательной системы  на угол на угол  то координаты то координаты  , ,  точки точки  через координаты через координаты  этой точки выражаются формулами (51), в которых этой точки выражаются формулами (51), в которых 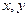 нужно заменить на нужно заменить на  , ,  : :
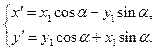 (52) (52)
Так как система координат  получена параллельным переносом получена параллельным переносом  , то координаты , то координаты 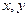 точки точки  в исходной системе выражаются через координаты в исходной системе выражаются через координаты  , ,  по формулам (48), в которых по формулам (48), в которых  нужно заменить на нужно заменить на  : :  В эти формулы вместо В эти формулы вместо  , ,  подставим (52) и получим подставим (52) и получим
 (53) (53)
Эти формулы выражают старые координаты 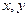 точки точки  через её новые координаты через её новые координаты  в новой системе. в новой системе.
Преобразования координат на плоскости применяются, в частности, для упрощения вида уравнений кривых. В системе координат  возьмём, например, эллипс с каноническим уравнением возьмём, например, эллипс с каноническим уравнением
 (54) (54)
Подставим вместо  их выражения (53) через их выражения (53) через  , тем самым получим уравнение эллипса в новой системе координат , тем самым получим уравнение эллипса в новой системе координат  . Это будет уравнение общего вида (после раскрытия скобок) . Это будет уравнение общего вида (после раскрытия скобок)
  . .
Таким образом, перейдя к системе  , от канонического уравнения (54) эллипса мы перешли к более сложному уравнению – уравнению второй степени общего вида. Можно показать, что, наоборот, от последнего уравнения в системе , от канонического уравнения (54) эллипса мы перешли к более сложному уравнению – уравнению второй степени общего вида. Можно показать, что, наоборот, от последнего уравнения в системе  , подобрав другую систему координат , подобрав другую систему координат  можно получить каноническое уравнение, определяющее либо окружность, либо эллипс, либо параболу, либо гиперболу, либо пару прямых, как, например, уравнение можно получить каноническое уравнение, определяющее либо окружность, либо эллипс, либо параболу, либо гиперболу, либо пару прямых, как, например, уравнение  ( ( , , 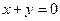 ), если не имеет место случай, когда уравнение определяет лишь точку или ничего не определяет. ), если не имеет место случай, когда уравнение определяет лишь точку или ничего не определяет.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|