|
|
Угловая скорость и угловое ускорениеСтр 1 из 6Следующая ⇒
Угловая скорость измеряется в радианах в секунду: [
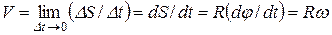 . (21) . (21)
Угловое ускорение характеризует быстроту изменения угловой скорости, т.е.
Оно связано с касательным ускорением формулой
Угловое ускорение измеряется в радианах на секунду в квадрате (рад / с2). С учетом формул (21) и (22) из формулы (19) находим
Л Е К Ц И Я № 2. Д И Н А М И К А М А Т Е Р И А Л Ь Н О Й Т О Ч К И Динамика – это раздел механики, посвященный изучению движения материальных тел под действием приложенных к ним сил. В основе динамики лежат 3 закона Ньютона, сформулированные в 1687 г. Они явились обобщением работ его предшественников и современников: Кеплера, Гюйгенса, Гука и др. 2.1. Первый закон Ньютона (закон инерции) Тело (материальная точка), не подверженное внешним воздействиям, либо находится в покое, либо движется прямолинейно и равномерно. Такое тело называют свободным, а его движение – свободным движением или движением по инерции. Свободных тел, строго говоря, не существует. Они являются физическими абстракциями. Свойство тел сохранять состояние покоя или равномерного прямолинейного движения называют инерцией тела. Количественной мерой инерции тела является его масса. Единицей массы в СИ является килограмм (кг). Обычно массу тела определяют, сравнивая ее с массой эталонных тел (гирь) путем взвешивания на рычажных весах. Первый закон Ньютона выполняется не во всех системах отсчета. Например, тела, лежащие неподвижно на гладком полу каюты движущегося равномерно и прямолинейно корабля, могут прийти в движение без всякого воздействия на них со стороны других тел, если корабль начнет изменять курс или скорость хода, т.е. когда корабль начнет двигаться ускоренно. Без указания системы отсчета закон инерции теряет смысл. Классическая механика постулирует, что существует система отсчета, в которой все свободные тела движутся прямолинейно и равномерно. Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной системой отсчета. Содержание закона инерции, в сущности, сводится к утверждению, что существует по крайней мере одна инерциальная система отсчета. Всякая система отсчета, движущаяся по отношению к инерциальной системе отсчета равномерно и прямолинейно, будет также инерциальной системой отсчета. Понятие инерциальной системы отсчета является научной абстракцией. С очень высокой точностью инерциальной можно считать гелиоцентрическую систему отсчета с началом в центре масс Солнца и осями, направленными на три звезды (такая инерциальная система отсчета используется в космонавтике). Лабораторная (земная) система отсчета неинерциальна главным образом из – за суточного вращения Земли. Однако, это вращение медленное
и для решения большинства технических задач инерциальной системой отсчета можно считать систему, жестко связанную с Землей. Закон инерции отнюдь не очевиден. До Галилея считали, что воздействие обуславливает не изменение скорости (т.е. ускорение), а саму скорость. Второй закон Ньютона Для того, чтобы его сформулировать введем понятие силы. Силой называется векторная величина, характеризующая воздействие на данное тело со стороны других тел. Сила Механическое воздействие может осуществляться как при непосредственном контакте тел (например, удар, трение, давление тел друг на друга и т.п.), так и между удаленными телами посредством гравитационных и электромагнитных полей. Для материальной точки справедливо следующее утверждение: ускорение, вызываемое силой, обратно пропорционально массе, т.е.
Это уравнение называется уравнением движения материальной точки. Оно будет
справедливо также и для поступательно движущихся тел, поскольку в этом случае ускорения всех точек тела будут одинаковыми, равными В классической механике масса материальной точки не зависит от скорости, а ускорение
или где – импульс материальной точки. В теоретической механике (а раньше и в физике), вектор Уравнение, записанное в форме (3), утверждает, что скорость изменения импульса материальной точки равна действующей на нее силе. Это утверждение называют вторым законом Ньютона, а соответствующее ему уравнение (3) – уравнением движения. Уравнение (3) дает также количественное определение силы: Второй закон Ньютона, записанный в форме (3), выражает принцип причинности в классической механике, т.к. устанавливает однозначную связь между изменением с течением времени состояния движения и положения материальной точки и действующей на нее силой. Этот закон позволяет, зная начальное состояние материальной точки (ее координаты и скорость в начальный момент времени) и действующую на нее силу, рассчитать состояние материальной точки в любой последующий момент времени. Из уравнений (2) и (3) следует, что при Таким образом, 1-й закон Ньютона, казалось бы, входит во второй закон как его частный случай. Несмотря на это, 1-й закон формулируется независимо от второго, поскольку в нем содержится утверждение о существовании в природе инерциальных систем отсчета. Из (1) следует, что Третий закон Ньютона Воздействие тел друг на друга всегда носит характер взаимодействия. Если тело 2 действует на тело 1 с силой Третий закон Ньютона утверждает, что силы взаимодействия двух материальных точек равны по модулю, противоположны по направлению и действуют вдоль прямой, соединяющей эти материальные точки:
Таким образом, силы всегда попарно возникают, они приложены к разным телам, и поэтому не могут уравновесить друг друга. Силы Все силы, встречающиеся в природе, сводятся к силам гравитационного притяжения, электромагнитным силам, слабым и сильным взаимодействиям. Сильные и слабые взаимодействия проявляются в атомных ядрах и в мире элементарных частиц. Они действуют на малых расстояниях: сильные – на расстояниях порядка 10-15 м, слабые - на расстояниях порядка 10-18 м. В макромире, который только и изучает классическая механика, от сильных и слабых взаимодействий можно отвлечься. В механике различают гравитационные силы, упругие силы и силы трения. Упругие силы и силы трения являются по своей природе электромагнитными.
Сила гравитационного взаимодействия двух материальных точек
Вес тела – это сила Упругие силы Они возникают при деформации тела и направлены в сторону обратную смещению (рис. 3). Для малых деформаций справедливо (закон Гука):
где k – коэффициент пропорциональности. Для пружины он называется коэффициентом жесткости, измеряется в Н/м. Силы трения
Трение, возникающее при относительном перемещении тел называется внешним трением; если при этом нет смазки, то трение называют сухим
 , (8) , (8)
т.е. сила трения пропорциональна величине силы нормального давления Трение между частями одного и того же сплошного тела (например, жидкости или газа) называется внутренним трением. Для него при небольших скоростях
где r – коэффициент сопротивления, имеющий размерность (кг/с).   Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? - задался я вопросом...  Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор...  Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот...  ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|