|
|
Отношения между простыми категорическими суждениями по истинности. Логический квадратВ разнообразных жизненных ситуациях бывает очень важно быстро формулировать и узнавать противоположные суждения, суждения, несовместимые с ранее высказанными и, наоборот, необходимо следующие из уже доказанных. Для этого нужно научиться оперировать отношениями суждений по истинности, изученными и систематизированными логикой. Если в одном суждении встречается хотя бы один термин, не входящий в другое суждение, то такие два суждения несравнимы. Примеры: "Все студенты - весёлые люди" и "Все студенты - находчивые люди". Суждения сравнимы, если их термины совпадают. Примеры: "Все студенты - весёлые люди" и "Ни один весёлый человек - не студент". Сравнимые суждения совместимы, если они могут быть одновременно истинны, и несовместимы, если не могут быть вместе истинными. В свою очередь, отношения совместимости делятся на отношения подчинения и субконтрарности, а отношения несовместимости - на отношения противоположности (контрарности) и противоречия (контрадикторности). Наглядно и системно эти отношения представлены в логическом квадрате. 1. Подчинение. Частные суждения подчиняются общим. Из этого следует: а) Истинность подчиняющего (общего) суждения обусловливает истинность подчинённого (частного). Примеры: Если верно, что "Ни одно сражение Суворова не было проиграно", то верно суждение "Некоторые сражения Суворова не были проиграны". То же для утвердительных суждений (А) и (I). б) Ложность подчинённого суждения влечёт ложность подчиняющего. Примеры: Если ложью является утверждение "Некоторые люди могут обходиться без воды и пищи", то, тем более ложным будет высказывание "Все люди могут обходиться без воды и пищи". Аналогично - отрицательные суждения (Е) и (О). в) Если подчиняющее суждение ложно, то об истинности подчинённого судить с необходимостью нельзя - оно может быть как истинным, так и ложным.
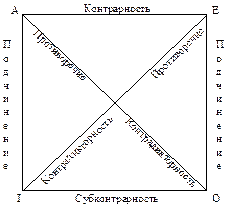
торые ученики готовятся ко всем урокам". 2. Субконтрарность. Отношение двух частных суждений (I) и (О) состоит в том, что они могут быть оба истинны, но не могут быть оба ложны. Пример: "Некоторые деревья зимой зелёные" и "Некоторые деревья зимой не зелёные" - оба суждения истинны. Субконтрарность проявляется в следующих отношениях: а) Если одно из субконтрарных суждений ложно, то другое необходимо истинно. Пример: Неверно, что "Некоторые учащиеся отказываются изучать логику". Значит, истинно, что "Некоторые учащиеся не отказываются изучать логику". б) Из истинности одного из субконтрарных суждений следует неопределённость истинности другого. Примеры: Истина: "Некоторые учебники нуждаются в серьёзной переработке", "Некоторые учебники не нуждаются в серьёзной переработке" -? Из истинности суждения: "Некоторые кошки не боятся собак" нельзя сделать вывод об истинности суждения "Некоторые кошки боятся собак". 3. Противоположность (контрарность). Отношения общих суждений (А) и (Е), которые не могут быть одновременно истинными, но бывают оба ложны. Примеры: "Все люди добрые", "Ни один человек не добрый" - два ложных преувеличения. а) Из истинности одного суждения следует ложность другого. Примеры: "Все выпускники умеют быстро читать" - истина, значит, "Ни один выпускник не умеет быстро читать" - ложь. Если "Ни одно высшее животное не уничтожает себе подобных" - истина, значит, ложно "Все высшие животные уничтожают себе подобных". б) Из ложности одного суждения следует неопределённость относительно истинности другого. Примеры: "Все инженеры пытаются создать вечный двигатель" - ложь; "Ни один инженер не пытается создать вечный двигатель" -? 4. Противоречие (контрадикторность). Отношение пар суждений (А) - (О) и (Е) - (I), выражающее закон исключённого третьего, т.е. истинность одного из них влечёт необходимо ложность другого, и наоборот, ложность одного - истинность другого. Примеры: Если истинно: "Некоторые птицы не летают", значит, ложно "Все птицы летают" и наоборот. Если ложно: "Ни один человек не боится смерти", значит, истинно "Некоторые люди боятся смерти". Сложные суждения Сложные суждения - это суждения, состоящие из двух и более простых суждений, соединённых логическими постоянными (связками). Логические постоянные (союзы) определяют виды сложных суждений и обозначаются символами: 1) конъюнкция - "и" (Ù) образует соединительное суждение (а Ù b); 2) дизъюнкция - "или" (v) образует разделительное суждение(а v b); 3) строгая дизъюнкция - "либо" (Ú) образует исключающе- разделительное суждение (а Ú b); 4) импликация - "если..., то" (®) образует условное суждение (а® b); 5) эквиваленция - "тогда и только тогда, когда" (º) образует равнозначное суждение (а º b); 6) отрицание - "неверно, что" - образует отрицательное сложное суждение (ā) или (a). Логические союзы могут соединять любое количество даже не связанных по смыслу суждений, истинность сложного суждения при этом будет зависеть только от истинности простых, составляющих его суждений и не будет зависеть от содержания, количества и качества этих суждений. Истинность и ложность сложных суждений устанавливается при помощи так называемых "таблиц истинности": 1. Соединительное суждение аÙ b (конъюнкция) Рассмотрим на примере такой ситуации: Я планирую свой день: "Прогуляю уроки и напишу реферат". Суждение а - "я прогуляю уроки". Суждение b - "я напишу реферат". Реально возможны 4 варианта осуществления плана, т.е. 4 комбинации истинности и ложности суждений а и в. Как при этом будет изменяться истинность сложного суждения (аÙb)?
а) Я прогулял уроки и написал реферат. План выполнен, сложное суждение оказалось истинным. б) Я прогулял уроки и не написал реферат - сложное суждение ложно, план не выполнен. в) Я всё-таки пошёл на уроки и ещё успел написать реферат - получилось не по плану, суждение также ложно. г) Я пошёл на уроки и не написал реферат - понятно, что план сорван, суждение ложно. Общий вывод - правило: конъюнкция истинна тогда и только тогда, когда истинны все входящие в неё простые суждения.
2. Разделительное (не исключающее) суждение а v b (дизъюнкция)
Пример: Ещё один план: "Или уеду в Италию, или уйду в монастырь". а - "я уеду в Италию"; b - "я уйду в монастырь". Снова 4 варианта: а) Решился, уехал в Италию, а там ушёл в монастырь - план перевыполнен, сложное суждение истинно. б) Уехал в Италию и забыл о монастырях. Поскольку планировалось одно из двух, суждение истинно. в) Не уехал в Италию, постригся в монахи. Суждение снова истинно. г) И уехать не собрался, и монахом стать не решился. Обещание не выполнено. Суждение ложно. Правило нестрогой дизъюнкции: суждения этого вида бывают ложными только в случае ложности всех составляющих простых суждений. 3. Исключающе-разделительное суждение а v b (строгая дизъюнкция). Смысл союза "либо" - утверждение несовместимости, противоречия составляющих суждений. Пример. Ситуация: ввиду очень пасмурной погоды возникает предположение: "Либо дождь пойдёт, либо снег". а - "пойдёт дождь", b - "пойдёт снег". а) Пошёл дождь вперемешку со снегом, т.е. дождь и снег. Союз "либо" не оправдался, суждение ложно. б) Дождь пошёл, снега нет. Предположение сбылось, суждение истинно. в) Вместо дождя пошёл снег. Произошло одно из двух. Суждение истинно. г) Тучи висят, но ни дождя, ни снега. Предположение, а вместе с ним и суждение, оказалось ложным. Правило: строгая дизъюнкция ложна, когда совпадают значения истинности входящих в неё простых суждений, и истинна, когда они различны.
4. Условное суждение а® b (импликация). Суждение а называется в импликации основанием, суждение b - следствием.
Пример: "Если много работать, можно многого добиться" (народная мудрость). а -"много работаешь", b - "добиваешься успеха". Как она проявляется в различных ситуациях: а) Некто много работал и действительно добился больших результатов. Суждение подтвердилось, импликация истинна. б) Некто много работал, но ничего не добился. Этот вариант опровергает истинность суждения, импликация ложна. в) Некто, не работая, всего добился. Несмотря на то, что основанием его успеха были не собственные усилия (ложность основания), результат (истинность следствия) говорит о том, что в целом суждение истинно. г) Некто ничего не делал и ничего не добился. Значит, народная мудрость была права, суждение истинно. Важный вывод: импликативное суждение бывает ложным тогда и только тогда, когда из истинного основания вытекает ложное следствие. Примеры: "Если 2 х 2 = 4, то снег чёрный" - ложь. "Если 2 х 2 = 5, то снег белый" - истина. "Если 2 х 2 = 5, то снег чёрный" - истина.
5. Эквивалентное суждение аº b (эквиваленция)
Пример суждения: "Человек свободен тогда и только тогда, когда он независим". а - "человек свободен"; b - "человек независим". В таком случае: а) Одновременно наличие свободы и независимости делает эквивалентное суждение истинным. б) Наличие свободы при отсутствии независимости согласно данному суждению - ложь. в) Также ложно и отсутствие свободы при наличии независимости. г) Нет свободы и нет независимости - эквивалентность истинна. Вывод: эквивалентные суждения истинны тогда и только тогда, когда значения истинности простых суждений совпадают.
6. Отрицательные суждения состоят из одного суждения и союза, его отрицающего. Поэтому таблица очень проста:
На основании закона исключённого третьего, если истинно, что "Наша власть демократическая", то утверждение "Неверно, что наша власть демократическая" - ложь. И наоборот. Сложные категорические суждения и выводы из них являются предметом логики высказываний. Другие сложные суждения и выводы из них исследуются модальной логикой. Модальные суждения Реальное общение осуществляется не только, и даже не столько через категорические высказывания (суждения), сколько посредством более содержательных по смыслу, разнообразных по интонации и более тесно связанных с культурно-историческими традициями и повседневными правилами поведения модальных суждений. Модальность (от лат. "modus" - мера, наклонение) - это характеристика особой связи между понятиями или суждениями данного высказывания. Эта связь может быть: сильной положительной - "необходимо", "обязательно", "доказано", "всегда", "хорошо", "известно", "лучше"; слабой - "случайно", "возможно", "проблематично", "сомнительно", " иногда", "неразрешимо", "равноценно", "безразлично"; сильной отрицательной - "опровергнуто", "невозможно", "никогда", "плохо", "хуже", "неизвестно", "запрещено". Слова, выражающие модальность, называются в логике, или модальными понятиями, или модальными операторами, или модальными функторами. Одним из первых обратил внимание на существование модальных суждений Аристотель. Он сформулировал ряд правил употребления модальных понятий "необходимо", "возможно", "случайно", "невозможно". В средние века У. Шервуд, У. Оккам, Ж. Буридан, занимаясь модальными выводами, говорили о функторах "действительно", "неизбежно", "истинно", "ложно", "неразрешимо", стремясь свести их к трём основным: "необходимость", "возможность", "невозможность". В восемнадцатом веке И. Кант по признаку модальности разделил все суждения на ассерторические (суждения действительности), аподиктические (суждения всеобщности и необходимости) и проблематические (суждения возможности). В современной логике общей теории модальных систем пока нет. В рамках символической (математической) логики разработано множество аксиоматических систем, использующих методы исчисления высказываний, связанных с многозначной и вероятностной логиками. По сферам применения все модальные понятия распадаются на группы, число которых, в принципе, не ограничено, но логика занимается лишь важнейшими из них. К ним относятся: Логическая модальность Логически необходимо любое высказывание, отрицание которого противоречит законам логики. Пример: Логически необходимо, что если идёт дождь, то идёт дождь. Логически возможно всё, что внутренне непротиворечиво. Если логически возможно как высказывание, так и его отрицание, т.е. не нарушены законы логики, то оно называется логически случайным. Пример: Логически возможно, что НЛО - явление внеземной разумной жизни. Логически невозможным является высказывание внутренне противоречивое. Пример: Логически невозможно, что если этот человек спит, то он не спит. Основными законами отношений логических модальностей являются: - если высказывание логически необходимо, то оно истинно, но не наоборот; - если высказывание логически необходимо, то оно логически возможно, но не наоборот; - если высказывание истинно, то оно логически возможно, но не наоборот. Законы логики, т.е. логически необходимые истины, являются абсолютно необходимыми, независимо ни от каких обстоятельств, они надприродны. Например, логически возможно, что люди ходят по потолку, хотя по природным законам это невозможно. Физическая модальность Физическую модальность называют также онтологической, т.е. присущей бытию, и каузальной (основанной на причинно-следственных закономерностях). Физически необходимо то, отрицание чего нарушает законы природы, т.е. невозможно физически. Пример: Физически необходимо, что всё живое рождается и умирает. Физически возможно высказывание, не противоречащее законам природы. При этом, если физически возможно как данное высказывание, так и его отрицание, то оно является физически случайным. Примеры: Физически возможно, что Кутузов одержал победу при Малоярославце. Физически случайно, что наш дом построен на горе. Физически невозможно высказывание, противоречащее природным законам. Пример: Физически невозможно, что крокодил беззубый, а ёжик без иголок. Правила взаимоотношений физических модальностей абсолютно аналогичны закономерностям логических модальностей. При этом, если сравнить логическую и физическую модальности между собой, то станет ясно, что самым широким модальным понятием является оператор "логически возможно" - за его пределами истин не существует. Значительно уже понятие "физически возможно" - оно ограничено законами нашего мира, т.е. всеми законами естественных наук. Объём физически необходимого ещё уже, это круг явлений и объектов, существующих реально. Самым узким модальным понятием является понятие "логически необходимо" - это только логические законы и всё, что из них необходимо следует. Очевидно, большая часть действительного мира живёт в рамках логически возможного, но за пределами логически необходимого. Логическую и онтологическую модальности называют алетическими (от греческого "алетос" - не скрытый, истинный, прямой). Эпистемическая модальность Эпистемическая модальность (от греч. "эпистема" - познание) выражает степень достоверности знания: доказано то, что получило научное обоснование и практическое подтверждение. Пример: Доказано, что сбалансированное питание благоприятно влияет на экстерьер собак; проблематично то, что на данный момент может оказаться как истинным, так и ложным. Пример: Вероятно, Россия - родина слонов; опровергнуто означает, что доказано обратное (противоречащее данному). Пример: Опровергнуто, что Сальери отравил Моцарта. Отношения эпистемических модальностей аналогичны алетическим. Основные их законы: - ничто не может быть доказанным и опровергнутым одновременно; - что доказано, то не может быть проблематично, и наоборот; - что проблематично, то не может быть опровергнуто, и наоборот; - "знание проблематично" означает, что это знание не доказано и не опровергнуто, и наоборот. Деонтическая модальность Деонтическая модальность (от греч. "деон" - долг, правильность) выражает логику норм или логику долженствования. Обязательно или нормативно необходимо всё, что вытекает из законов и норм общества. Пример: Обязательно выполнять военные команды, соблюдать правила уличного движения и платить налоги. Разрешено любое действие, не являющееся ни нормативно обязательным, ни нормативно запрещённым. Пример: Разрешено обедать дома без галстука. Запрещено всё, что противоречит нормативно обязательному и то, что является предметом нормативного запрета. Примеры: Запрещено не платить налоги. Запрещено курить в салоне для некурящих. Законы отношений деонтических модальностей аналогичны эпистемическим, но если познавательные истины являются всеобщими, то деонтические высказывания уместны только в пределах данной нормативной системы права, религии, морали и т. п., и с точки зрения другой системы могут быть отвергнуты.   Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот...  Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...  ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между...  Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|