|
|
Особые случаи короткого трубопровода ⇐ ПредыдущаяСтр 3 из 3 Истечение трубопровода под уровень. В этом случае уравнение Бернулли будет иметь несколько иной вид. Выбираем плоскость сравнения 0-0 таким образом, что все сечения трубопровода лежат на плоскости. Выбираем расчетные сечения: 1-1 - по свободной поверхности жидкости в напорном резервуаре, 2-2 - по свободной поверхности жидкости в приемном резервуаре. Запишем исходный вид уравнения Бернулли: z1 + P1/γ+α1V21 /2g=z2+P2/γ +α2V22/2g+∑h1-2. В сечениях 1-1 и 2-2 известны следующие величины (cм. рис. 50): Z1=H1, P1=Pатм, V1=0, (так как приток и отток из резервуара равны между собой), Z2=H2, P2=Ратм, V2=0. Таким образом, после подстановки указанных величин в исходное уравнение, получим конечный вид уравнения Бернулли для случая, представленного на рисунке 50: H1+ Pатм./γ= H2+ Pатм./γ+∑h1-2, H1=H2+∑h1-2. В уравнении пока неизвестны потери напора (∑h1-2). Они рассчитываются аналогично потерям в простом гидравлически коротком трубопроводе.
Сифонный трубопровод. Сифонным трубопроводом (сифоном) называют самотечную трубу, часть которой расположена выше горизонта жидкости в сосуде, который ее питает (рис. 51). Ограничимся рассмотрением истечения из сифона под уровень. Для действия сифона из него необходимо предварительно удалить воздух и создать в нем первоначальное разрежение. После заполнения его жидкостью начнется движение из верхнего сосуда в нижний. Движение происходит под действием разности уровней.
Рисунок 51 - Сифонный трубопровод.
В том, что жидкость в такой трубе будет двигаться, можно убедиться из следующего. Наметим сечение трубы n-n и обозначим превышение его над горизонтом жидкости: в левом сосуде – через h1, в правом сосуде – через h2. Если предположить, что жидкость, заполняющая сифон, находится в покое, то можно написать: - давление в сечении n-n с левой стороны p1= pатм – h1γ - давление в сечении n-n с правой стороны p2=pатм – h2γ Как видно, p1> p2 (т.к. h1 < h2); отсюда понятно, что жидкость в трубе не может находиться в покое: она будет двигаться слева направо, т.е. в сторону меньшего давления. Характерным для сифона является то, что в нем имеет место вакуум. Наибольшая величина вакуума будет в сечении, наиболее высоко расположенном, т.е. в сечении n-n. Найдем максимальную величину вакуума (hвак)max в сифоне. С этой целью наметим по линии n-n, где ищем вакуум, сечение 2-2 и составим уравнение Бернулли для сечения 1-1 (проходящим по уровню жидкости в питающем сосуде) и 2-2. Плоскость сравнения 0-0 расположим также по уровню жидкости в левом сосуде. Тогда общий вид уравнения можно преобразовать следующим образом: z1+ P1/ γ + α1V12/2g=z2+P2/γ+α2V22/2g + ∑h1-2. z1=0; P1/γ=Pатм/γ; α1V12/2g=0; V1≈0 z2=h1; P2/γ=Pn/γ; α2V22/2g=αV2/2g; где: V - скорость в трубе; pn - давление в сечении n-n. Pатм/γ=h1+Pn/γ+αV2/2g+∑h1-n Потери напора можно определить по обычной формуле: ∑h1-n=ζ!×V2/2g, где: ζ!= (ζ+λ L/d) – общий коэффициент сопротивления системы. После преобразования получим следующий вид уравнения: Pатм/γ-Pn/γ=h1+αV2/2g+(ζ+λL/d)V2/2g. Но Pатм/γ-Pn/γ=(hвак)макс, Тогда (hвак)макс = h1+αV2/2g+(ζ+λL/d)V2/2g. По этой формуле можно рассчитывать вакуум в любом сечении трубы, но (hвак)макс должен быть меньше допускаемого (hвак)доп, в противном случае может возникнуть кавитация. Обычно (hвак)доп = 6-7 м. вод. ст.
Расчет сложного трубопровода К числу элементов сложного трубопровода можно отнести следующие: последовательное соединение труб разного диаметра; параллельное соединение; трубопровод с переменным по пути расходом; кольцевой трубопровод; разомкнутая сеть. Последовательное соединение При последовательном соединении трубопроводов различного диаметра исходят из того, что общие потери напора в трубопроводе равны сумме потерь напора на отдельных его участках. Допустим, что диаметры участков di различные, тогда общие потери напора равны сумме потерь на отдельных участках: H=h1+ h2+ …+hп. Для гидравлически короткого трубопровода потери определяются по формулам Вейсбаха и Дарси-Вейсбаха, а для гидравлически длинного трубопровода потери определяются по
где К – модуль расхода. Или для всего трубопровода
Рисунок 52 - Схема последовательного соединения и построения характеристики Часто используется графо-аналитические методы с построением гидравлических характеристик участков и сети, особенно при переменном расходе в сети. Характеристикой трубопровода или участка называется графическая зависимость потерь напора (давления) в трубопроводе от расхода жидкости hп=f(Q). Изобразим эту зависимость графически (рис.52). Для построения характеристики hп=f(Q) необходимо рассчитать 5-7 точек кривой. При расчете последовательно соединенных трубопроводов необходимо помнить, что по всем участкам такого трубопровода протекает одинаковый расход. Кривая I соответствует гидравлической характеристике первого участка, кривая II – второго участка. Так как общие потери во всем трубопроводе равны сумме потерь напора на двух участках, а расходы на участке 1 и участке 2 одинаковы, то для построения суммарной характеристики сложного трубопровода с последовательным соединением необходимо сложить гидравлические характеристики отдельных участков. При этом суммарную (общую) характеристику такой сети строят сложением ординат кривых I и II, представляющих собой характеристики hп=f(Q) соответственно для 1-го и 2-го участков. Для этого проведем ряд прямых, параллельных оси ординат, каждая из которых пересечет обе кривые, и сложим ординаты точек пересечений этих прямых с кривыми. Получим ряд точек a,b,c, принадлежащих новой кривой I+II, которая представляет собой искомую суммарную характеристику всего рассматриваемого трубопровода (сети).
Параллельное соединение Параллельно соединенные трубопроводы имеют общую точку разветвления и общие узлы соединения. При расчете трубопровода с параллельными ветвями исходят из того, что сумма расходов в отдельных ветвях равны полному расходу Q1+Q2+…+Qn=Q и что потери напора во всех ветвях одинаковы h1=h2=…=hn. Докажем это положение.
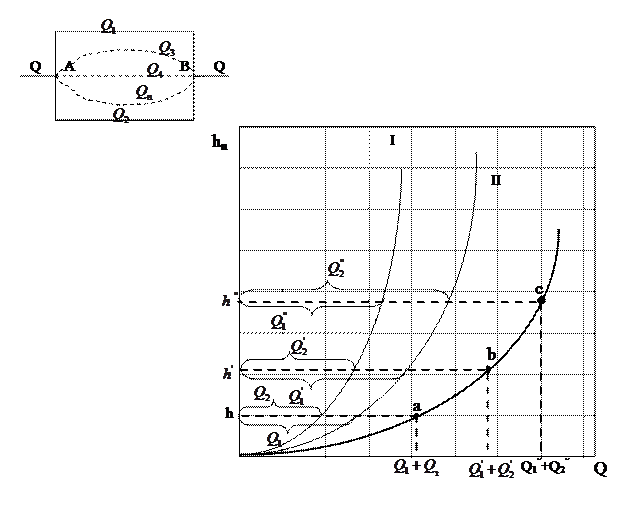
Рисунок 53 - Схема параллельного соединения и построения характеристики
В точке А магистральный расход делится на n веток, которые объединяются в точке В, образуя далее продолжение магистрали трубопровода. Напоры HA и HB в точках А и В являются общими для каждой из веток, а их разность
одновременно для каждой из веток:
или
В системе n уравнений и n+1 неизвестных Порядок решения таков: все расходы выразим через один из них.
после чего получим
Отсюда найдем расход При расчете трубопровода с параллельным соединением ветвей также удобно применять графо-аналитический способ с построением гидравлической характеристики сети трубопроводов. Эта характеристика получается путем сложения гидравлических характеристик отдельных труб, для чего необходимо провести ряд горизонтальных прямых (т.к. потери Покажем построение суммарной характеристики такой сети (рис. 53). Сложим ординаты кривых I и II, представляющих собой характеристики hn=f(Q) соответственно для 1-го и 2-го участков. Для этого проведем ряд прямых, параллельных оси ординат, каждая из которых пересечет обе кривые, и сложим ординаты точек пересечений этих прямых с кривыми, получим ряд точек a,b,c, принадлежащих новой кривой I+II, которая представляет собой искомую суммарную характеристику всего рассматриваемого трубопровода (сети). Таким образом, для построения суммарной характеристики сложного трубопровода необходимо сложить характеристики отдельных участков при параллельном соединении по горизонтали, а при последовательном по вертикали. Часто сеть трубопроводов имеет как последовательно, так и параллельно соединенные участки. В этом случае для получения характеристики сети рекомендуется сначала получить суммарную характеристику параллельно соединенных участков, а затем сложить ее с характеристиками последовательно соединенных участков, На рисунке 54 приведен пример такого построения. Линия 1 – характеристика 1-го участка, линии 2-3 – характеристики 2-го и 3-го участков, соответственно. Линия 4 – суммарная характеристика двух параллельно соединенных участков (2+3), а линия 5 – общая характеристика сети.
Рисунок 54 - Схема сложного соединения и построение характеристики.
  Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...  Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...  Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все...  Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|
Рисунок 50 - Трубопровод с истечением под уровень.
формуле:
,
,
,
.
. Для замыкания системы требуется еще одно уравнение: 
; 
; ……; 
;
.
, а затем и остальные расходы.
= hn), параллельных оси абсцисс, и сложить при постоянных ординатах абсциссы точек их пересечения с характеристиками отдельных участков (т.к. 
).