|
Алгоритм решения канонической задачи ЛП симплексным методом (метод Данцига).
Основная задача ЛП называется канонической, если система уравнений каноническая, а целевая функция выражена через свободные неизвестные.
Рассмотрим алгоритм решения канонической задачи ЛП симплексным методом:
Дано:общая задача ЛП
Минимизировать 
при условиях:

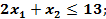

 ; ;

Это общая задача ЛП. Переходим к каноническому виду:

При условиях
 ; ;



 . .
Здесь  , а , а  переменные. Задача ЛП каноническая. Нетрудно убедиться, что r(A) = r(R), т.е. система ограничений совместна. Кроме того, r(A) = 4, n = 6. Составим исходную симплексную таблицу. переменные. Задача ЛП каноническая. Нетрудно убедиться, что r(A) = r(R), т.е. система ограничений совместна. Кроме того, r(A) = 4, n = 6. Составим исходную симплексную таблицу.
Исходная симплексная таблица
Базисные переменные

| Свободные члены

| Коэффициенты при неизвестных
| 
| 
| 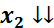
| 
| 
| 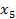
| 
| |
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
| | F
|
|
|
|
|
|
|
|
|
Пустые клетки соответствуют нулям. Столбец контрольной суммы ( ) включает в себя алгебраические суммы коэффициентов каждой строки и служит для контроля арифметических действий при последующем преобразовании данной таблицы. Последняя строка таблицы называется индексной. При ее заполнении свободный член целевой функции выписывается со своим знаком, а коэффициенты при неизвестных (оценки) – с противоположным. Выберем так называемый разрешающий столбец с положительной оценкой. Но таких столбцов два. Выбираемстолбец с оценкой 5. Далее выбирается так называемая разрешающая строка. Из отношений свободных членов к положительным коэффициентам разрешающего столбца ( ) включает в себя алгебраические суммы коэффициентов каждой строки и служит для контроля арифметических действий при последующем преобразовании данной таблицы. Последняя строка таблицы называется индексной. При ее заполнении свободный член целевой функции выписывается со своим знаком, а коэффициенты при неизвестных (оценки) – с противоположным. Выберем так называемый разрешающий столбец с положительной оценкой. Но таких столбцов два. Выбираемстолбец с оценкой 5. Далее выбирается так называемая разрешающая строка. Из отношений свободных членов к положительным коэффициентам разрешающего столбца ( ) выбираем наименьшее т.е. ) выбираем наименьшее т.е.  . Это отношение и соответствует разрешающей строке.Коэффициент 3, находящийся на пересечении разрешающей строки и разрешающего столбца, называется разрешающим элементом. Выведем . Это отношение и соответствует разрешающей строке.Коэффициент 3, находящийся на пересечении разрешающей строки и разрешающего столбца, называется разрешающим элементом. Выведем  из базиса, а из базиса, а  (провокатор) введем в базис. В результате получим новые наборы базисных и свободных переменных. Необходимо выразить базисные переменные и целевую функцию через свободные переменные. Для этогоразрешающую строку в исходной симплексной таблице делим на разрешающий элемент. Результат заноситься в новую симплексную таблицу “Итерация 1”. (провокатор) введем в базис. В результате получим новые наборы базисных и свободных переменных. Необходимо выразить базисные переменные и целевую функцию через свободные переменные. Для этогоразрешающую строку в исходной симплексной таблице делим на разрешающий элемент. Результат заноситься в новую симплексную таблицу “Итерация 1”.
Итерация 1
| Базисные переменные
| Свободные члены
| Коэффициенты при неизвестных
|
| 
| 
| 
| 
| 
| 
| 
| 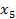
| 
|
| 
|
|
|
|
|
| -1
|
|
| 
|
|
|
|
|
| -1/3
|
| 32/3
| 
|
|
|
|
|
| 1/3
|
| 19/3
| 
|
|
|
|
|
|
|
|
| | F
| -25
|
|
|
|
| -5/3
|
| -59/3
|
Коэффициенты данной симплексной таблицы вычисляются таким образом, чтобы в разрешающем столбце исходной таблицы все элементы, кроме разрешающего, стали нулевыми. Например, для того что бы в исходной таблице в уравнении 2  +3 +3  + +  =19 получить коэффициент при =19 получить коэффициент при  нуль, надо третью строку в таблице «Итерация 1» умножить на (-3) и сложить с первой строкой исходной таблицы. Результат записывается в первую строку таблицы «Итерация 1». Получим 2 нуль, надо третью строку в таблице «Итерация 1» умножить на (-3) и сложить с первой строкой исходной таблицы. Результат записывается в первую строку таблицы «Итерация 1». Получим 2  + +  - - 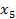 =4, откуда базисное переменное =4, откуда базисное переменное  легко можно выразить через свободные переменные. Аналогично вычисляется в этой строке и контрольная сумма: ( легко можно выразить через свободные переменные. Аналогично вычисляется в этой строке и контрольная сумма: ( . Алгебраическим сложением коэффициентов строки убеждаемся, что арифметической ошибки нет.В полученной таблице «Итерация 1» выбирается положительная оценка. В частности, столбец, соответствующий оценке 7, будет разрешающим. Затем выбирается разрешающая строка и т.д. Столбец контрольной суммы для простоты можно опустить. Продолжим решение.В итоге получим следующие симплексные таблицы: . Алгебраическим сложением коэффициентов строки убеждаемся, что арифметической ошибки нет.В полученной таблице «Итерация 1» выбирается положительная оценка. В частности, столбец, соответствующий оценке 7, будет разрешающим. Затем выбирается разрешающая строка и т.д. Столбец контрольной суммы для простоты можно опустить. Продолжим решение.В итоге получим следующие симплексные таблицы:
Итерация 2
Базисные переменные

| Свободные члены

| Коэффициенты при неизвестных
| 
| 
| 
| 
| 
| 
| 
|
|
|
| 1/2
|
| -1/2
|
| 
|
|
|
| -1
|
| 2/3
|
| 
|
|
|
|
|
| 1/3
|
| 
|
|
|
| -3/2
|
| 3/2
|
| | F
| -39
|
|
| -7/2
|
| 11/6
|
|
Итерация 3
Базисные переменные

| Свободные члены

| Коэффициенты при неизвестных
| 
| 
| 
| 
| 
| 
| 
|
|
|
| -1/4
| 3/4
|
|
| 
|
|
|
| -3/2
| 3/2
|
|
| 
|
|
|
| 1/2
| -1/2
|
|
| 
|
|
|
| 3/4
| -9/4
|
|
| | F
| -50
|
|
| -3/4
| -11/4
|
|
|
Выписав из последней симплексной таблицы выражение для целевой функции  убедимся, что базисное решение убедимся, что базисное решение 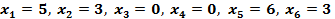 является оптимальным (все оценки в индексной строке отрицательны), а является оптимальным (все оценки в индексной строке отрицательны), а 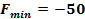 . .
Решая задачу максимизации  при тех же условиях, что и раньше, получим при тех же условиях, что и раньше, получим 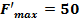 . Оптимальное решение этой задачи оптимизации совпадает с оптимальным решением задачи минимизации . Оптимальное решение этой задачи оптимизации совпадает с оптимальным решением задачи минимизации  . .
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




