|
|
Формула сложения вероятностей. ⇐ ПредыдущаяСтр 2 из 2
U - достоверное событие
Покажем, что события * Если события несовместны, то т.е. события несовместны. Тогда по третей аксиоме теории вероятности
Справедливо следующее тождество на основании (1) и закона дистрибутивности
Показать самим, что все три множества попарно несовместны.
На основании первой и третей аксиомы теории вероятности получаем:
Имеет место тождество
По третей аксиоме:
Для экзамена доказать самим формулу суммы произвольного числа событий
Формула полной вероятности. Рассмотрим систему A из k попарно несовместных событий. B1, B2,..., Bk Пусть дано событие A, удовлетворяющее равенству A=B1A+B2A+...+BkA. Показать, что события B1A, B2A, BkA попарно несовместны. BiABjA=BiBjAA=VAA=V Найти вероятность наступления события A. Любое событие входящее в A, обязательно входит в некоторое, но одно Bi, т.к. B1, B2,..., Bk образуют полную группу. Т.к. B1, B2,..., Bk несовместны, то по третей аксиоме теории вероятности имеем:
Например: Имеются урны трех составов
Все шары в каждой урне перемешаны. Испытание - извлекается шар. Какая вероятность того, что при этом будет извлечен белый шар. B1 - Вытащить любой шар из урны 1. B2 - Вытащить любой шар из урны 2. B3 - Вытащить любой шар из урны 3. A - Извлечь белый шар. A=B1A+B2A+B3A B1, B2, B3 - попарно несовместны. Формула полной вероятности: P(A)=P(B1)P(A/B1)+P(B2)P(A/B2)+P(B3)P(A/B3)
P(A)=1/3×2/3+1/5×11/10+7/15×0=2/9+2/11=40/99»0.4 Формула Байеса. Постановка задачи та же, но решаем обратную задачу. Проводится испытание, в результате которого произошло событие A. Какова вероятность того, что в этом испытании произошло событие Bi. Условные вероятности называются апостериорными, а безусловные - априорными вероятностями. P(ABi)=P(A)P(Bi/A)=P(Bi)P(A/Bi) Откуда, Таким образом, формула Байеса: Композиция испытаний. Имеется вероятностное пространство, которое порождает испытание 1.
где Ei, i=1,..., m1 - пространство элементарных событий в результате испытания. P(Ei), i=1,..., m1 - вероятности элементарных событий. Испытание 2 порождает вероятностное пространство вида
P(Ei), P(Qj) - разные вероятностные меры. Композицией двух испытаний называется сложное испытание, состоящее в поведении первого и второго испытания. Композиция испытаний порождает вероятностное пространство вида:
EiQj - композиционное событие. В общем случае по P(Ei) и P(Qj) найти P(EiQj) невозможно. Рассмотрим один частный случай, когда это можно сделать. Два испытания называются независимыми, если различные исходы обоих испытаний определяются несвязанными между собой случайными факторами. Из определения независимости испытания вытекает, что условные частости наступления события в одном испытании, при условии, что во втором испытании произошло фиксированное число событий равны безусловным частостям, если они существуют. Пусть испытания независимы. В результате проведения первого испытания произошло элементарное событие Ei, в результате второго испытания может произойти все что угодно. Тогда сложное событие, определяющее исход первого и второго испытания имеет вид:
Вероятность сложного события A.
Если в результате второго испытания произошло событие Qj, а в результате первого испытания могло произойти все что угодно, то сложное событие B имеет вид: Вероятность сложного события B равна сумме вероятностей комбинаций вида EiQj, i=1,..., m1
A={EiQ1, EiQ2,..., EiQj,..., EiQm2} B={E1Qj, E2Qj,..., EiQj,..., Em1Qj} По определению произведения AB в него входят только те события, которые входят и в A, и в B. Из приведенных выше формул следует, что только событие EiQj входит и в A, и в B, то AB= EiQj. Следует:
Композиционное пространство имеет вид: Общая структура независимых событий в композиционном пространстве, порожденном композицией испытаний:
т.е. в результате первого испытания произошли элементарные события: В результате второго испытания события: Сложное событие B определяет все возможные комбинации исходов двух испытаний независимо друг от друга. В результате первого испытания произошли элементарные события: В результате второго испытания события: Тогда:
т.к. то При решении практических задач, связанных с независимыми испытаниями обычно не требуется строить композиционных пространств элементарных событий, а использовать формально неверную запись: P(A×B)=P(A)×P(B). Композиция n испытаний. Имеется n испытаний. Зададим для i-го испытания вероятностное пространство:
Композицией n испытаний называется сложное испытание, состоящее в совместном проведении n испытаний. Задается n испытаний, вероятностное пространство каждого из которых имеет вид:
Композиционное пространство имеет вид:
Композиция n независимых испытаний. Испытания (n - испытаний) называются независимыми, если неоднозначность исхода каждого из испытаний определена не связанными между собой группами факторов. Событие A1: в результате проведения композиционного испытания в первом испытании произошло событие Событие An: в результате проведения композиционного испытания в первом испытании произошло событие
Рассмотрим событие: В силу определения независимости испытаний очевидно, что:
Следовательно: На практике не строят композиционных пространств, а записывают формально неправильную формулу: P(A1A2...An)=P(A1)P(A2)...P(An). Композиционное пространство имеет вид:
Общая структура независимых событий в композиционном пространстве имеет вид:
Рассмотрим два вероятностных пространства.
Очевидно, что неопределенность испытания до испытания в первом вероятностном пространстве выше, чем во втором. Действительно, до испытания в I нельзя ни одному из событий отдать предпочтения, а во II событие E3 происходит чаще. Энтропия - мера неопределенности исхода испытания (до испытания).
Первым, кто функционально задал выражение для энтропии был Шеннон.
Для вероятностного пространства:
Энтропия задается выражением: Самим показать, что: Если вероятностное пространство не имеет определенности, т.е. какое-то из Pi=1, а остальные равны 0, то энтропия равна нулю. Если элементарный исход равновероятен, т.е. 0£Pi£1, 1)
т.о. вероятности p1, p2,..., ps обращаются в ноль, например pi, которая равна 1. Но log1=0. Остальные числа также обращаются в 0, т.к. 2) Докажем, что энтропия системы с конечным числом состояний достигае максимума, когда все состояния равновероятны. Для этого рассмотрим энтропию системы как функцию вероятностей p1, p2,..., ps и найдем условный экстремум этой функции, при условии, что Пользуясь методом неопределенных множителей Лагранжа, будем искать экстремум функции: Дифференцируя по p1, p2,..., ps и приравнивая производные нулю получим систему:
Откуда видно, что экстремум достигается при равных между собой p1. Т.к. Еденицей измерения энтропии является энтропия вероятностного пространства вида:
Неопределенность исхода испытания до испытания автоматически определяет информативность исхода испытания после испытания. Поэтому в битах также измеряется информативность исхода. Рассмотрим два вероятностных пространства:
Проводим композицию двух испытаний. Композиционное пространство имеет вид:
С точки зрения качественного анализа максимальная энтропия композиционного вероятностного пространства достигается тогда, когда испытания независимы. Найдем энтропию композиционного пространства для случая независимых испытаний.
Биномиальное распределение. n испытаний называются системой испытаний Бернулли, если испытания независимы, в каждом из них происходит событие Найдем вероятность того, что в результате проведенных n испытаний событие А произошло m раз:
Рассмотрим композицию n независимых испытаний и построим композиционное пространство элементарных событий. Общий вид элемента этого пространства следующий:
При этом вероятность наступления такого события равна:
Найдем вероятность наступления любого элементарного события из композиционного пространства:
Рассмотрим в композиционном вероятностном пространстве событие: в n испытаниях событие A произошло m раз. Событие A состоит из
Следовательно, на основании III аксиомы теории вероятности результат равняется:
Случайная величина
Пусть имеется вероятностное пространство вида Случайной величиной называется измеримая числовая скалярная функция Числовая скалярная функция - это функция, удовлетворяющая следующему условию:
Если произведено испытание, в результате которого произошло некоторое элементарное событие В соответствии с определением случайной величины вводится числовая скалярная функция F(x),
Эта функция называется функцией распределения случайной величины Рассмотрим три события:
где a<b, a, b - действительные числа. Свойства:
Покажем, что из факта A2 Ì s-алгебре A1 Ì s-алгебре и равенства
По определению s-алгебры A3 измерима, поэтому можно принять III аксиому теории вероятности:
F(x) - неубывающая функция Если x<y, то
т.к. Для всех технических приложений функцию распределения можно считать направленной слева. В силу того, что функция распределения не убывает, она однозначно задает стчетно-аддитивную меру на поле, порожденном всеми полуинтервалами ненулевой длины. По введенному полю построим борелевскую алгебру. Обозначим ее b. Возьмем произвольное число BÌb не принадлежащее полю. Это точка или сегмент. Т.к. множество Функция
где
Функция g(x) называется борелевской функцией, если для любого BÌb множество
Борелевская функция - функция, определяемая на системе борелевских множеств. В функциональном анализе показано, что все известные аналитические функции являются борелевскими. ТЕОРЕМА: Пусть g(x) борелевская функция,
является измеримой и, следовательно, случайной величиной. Берем произвольное BÌb. Рассмотрим множество
т.к. Следовательно, функция Теорема Колмогорова
Любая числовая скалярная функция, которая удовлетворяет свойствам, которым удовлетворяет функция распределения, является функцией распределения и однозначно задает вероятностное пространство вида:
b - борелевская алгебра; P - мера на борелевской алгебре; R1 - числовая скалярная ось. Введем функцию F(x)
Эта функция определена для всех x, неубывающая, непрерывная сверху. Показать самим, что такая функция однозначно задает счетно-аддитивную меру на поле, порожденном всеми полуинтервалами ненулевой длины. Докажем, что 0<F(x)<1 Согласно терминологии, если функция y=f(x) непрерывна на отрезке [a, b], то она ограничена. Поскольку наша функция не убывающая, то максимум и минимум она соответственно будет иметь такой:
т.е. 0<F(x)<1.
2. Пусть имеем следующие функции. Построим борелеву алгебру на поле, тогда по теореме о продолжении счетно-аддитивная функция, определенная на поле, без изменения аксиом теории вероятности, однозначно распространяется на все элементы борелевой алгебры, не принадлежащие полю. Т.о. вероятностное пространство построено, теорема доказана. Смысл теоремы. Теорема Колмогорова позволяет утверждать, что если вы исследуете случайную величину, то не надо строить абстрактное пространство элементарных событий, s-алгебру, счетно-аддитивную меру, конкретный вид функции X1, X2,..., Xn Дискретные случайные величины
Случайная величина называется дискретной, если в результате испытания она может принять значение из конечного либо счетного множества возможных числовых значений. Случайные величины в дальнейшем будем обозначать большими буквами: X, Y, Z Вероятностное пространство дискретной случайной величины задается в виде:
Пример: Испытание - композиция n-независимых испытаний, в каждом из которых происходит событие A с вероятностью p, либо Вероятностное пространство
В этом примере s-алгеброй является множество всех подмножеств пространства элементарных событий. Введенную нами случайную величину x по определению можно задать:
- верхняя строчка - это совокупность возможных числовых значений, которые может принимать случайная величина; - нижняя строчка - вероятность наступления этих числовых значений. Практически во всех задачах естествознания отсутствует промежуточный этап: испытание, W - пространство всех возможных исходов испытания, На самом деле структура: - испытание; - исход испытания; - число на числовой оси. Вероятностные характеристики дискретных случайных величин.
Математическим ожиданием случайной величины X называется число вида
xi - все возможные различные конкретные исходы испытания; pi - вероятности их наступления. Математическое ожидание является как бы аналогом центра масс точечной механической системы:
Как центр масс:
Смысл характеристики мат.ожидания заключается в следующем: это точка на числовой оси, относительно которой группируются результаты конкретных испытаний над дискретной случайной величиной. Свойства математического ожидания
1. MC=C
2. MCX=CMX Построим таблицу для случайной величины CX:
по определению математического ожидания:
3. M(X+a)=MX+a, a=const Построим таблицу для случайной величины x+a
Доказать следствие
4. M(aX+b)=aMX+b, где a, b - константы
Пусть случайная величина Y является функцией f(x) от случайной величины X. Построим вероятностное пространство случайной величины Y.
Верхняя строчка является пространством элементарных событий для случайной величины Y. В противном случае верхняя строчка является пространством элементарных событий для величины Y. Все одинаковые числа в верхней строчке заменяется одним, вероятность наступления которого равна сумме соответствующих вероятностей. Следствие. Математическое ожидание случайной величины Y равняется:
Начальным моментом К-го порядка случайной величины X называется математическое ожидание случайной величины Xk.
Центрированная случайная величина - это величина, равная X’=X-MX Покажем, что математическое ожидание MX’ равно 0.
Центральным моментом К-го порядка называется начальный момент К-го порядка случайной величины X’
при решении реальных задач практические вероятности рi неизвестны, но считая, что вероятность - это частость, при большом числе испытаний
Дисперсией случайной величины X, называется центральный момент второго порядка случайной величины X.
Дисперсия является мерой концентрации результатов конкретных испытаний над случайной величиной X. Свойства. 1. Чем меньше дисперсия, тем более тесно группируются результаты конкретных испытаний относительно математического ожидания. Пусть дисперсия мала, тогда мало каждое слагаемое суммы (xi-n)2pi. Тогда для, xi которое по модулю резко отличается от математического ожидания n, pi - мало. Следовательно, большую вероятность наступления могут иметь лишь те xi, которые по модулю мало отличаются от математического ожидания.
2. Если дисперсия равна 0, то X - const.
3. D(X+C)=DX Y=X+C Y’=Y-MY=X+C-M(X+C)=X+C-MX-C=X-MX=X’ DY=M(Y’)2=M(X’)2=DX
4. DCX=C2DX Y=CX DY= M(Y’)2=M(Y’)2 Y’=Y-MY=CX-MCX=CX-MCX=C(X-MX)=CX’ DY= M(Y’)2=M(CX’)2=C2M(X’)2=C2DX
5.
Построим функцию распределения для дискретной случайной величины. Для удобства договоримся, что случайные величины располагаются в порядке возрастания.
т.е. по определению для любого действительного X, F(x) численно равно вероятности наступления следующего события: в результате испытаний над X оно приняло значение строго меньше x.
Производная функция
Характеристической функцией случайной величины X называется функция действительного аргумента вида Производящей функцией называется скалярная функция вида:
Свойства производящей функции
1.
2.
3. Разложение производящей функции в ряд Маклорена имеет вид
Формула Тейлора имеет вид
при to=0 она носит название формулы Маклорена
Пример: Рассмотрим случайную величину, распределенную по биноминальному закону распределения:
Найдем производящую функцию:
Найти DX и MX
Первая модель распределения Пуассона
Проведена неограниченно большая серия испытаний, в результате каждого испытания случайным образом появляется точка на числовой оси. Случайное распределение точек на числовой оси удовлетворяет следующим трем свойствам. 1. Стационарность. Вероятность того, что на отрезок данной длины попадает данное количество точек определяется только длиной этого отрезка и не зависит от расположения этого отрезка на числовой оси. 2. Ординарность. Вероятность того, что на достаточно малый отрезок длины Dx попадает одна точка, является бесконечно малой Dx порядка. Вероятность того, что на этот отрезок попадает более, чем одна точка, является бесконечно малой более высокого порядка, чем Dx. 3. Свойство без последействия. Вероятность того, что на данный отрезок попало определенное количество точек не зависит от того, сколько точек в результате проведенной бесконечно серии испытаний попало на отрезок, не пересекающийся с данным. Найти вероятность того, что на данный отрезок длина l попадает m точек.
Обозначим через xl - случайная величина, равная численности точек, выпавших на отрезок длины l.
На числовой оси рассмотрим отрезок длины 1 и обозначим: MX1=l Математическое ожидание числа точек, попавших на отрезок длины 1. По свойству стационарности l одинаково для всех отрезков.
MX1=ll - доказать Пусть l - целое число. Разобьем отрезок длины l на l отрезков единой длины. Тогда количество точек, попавших на отрезок длины l будет равно числу точек, попавших на каждый из непересекающихся отрезков длины 1 (тут использовалось свойство беспоследействия). Используя формулу
имеем MX1=ll Математическое ожидание числа точек, попавшие на отрезок длины l равно мат. ожиданий точек, попавших на непересекающиеся отрезки. Пусть l - не целое число. Выделяем целую часть. Тогда
На числовой оси рассмотрим отрезок длины l, разобьем его на n отрезков данной длины
такой, что позволит использовать свойство ординарности. Тогда с определенной погрешностью, которая тем меньше, чем больше n можно считать
т.е. на отрезок длины Dx попадает не более, чем одна точка, тогда
Для достаточного малого отрезка длины lDx вероятность попадания в него одной точки Dx, а вероятность того, что ничего не произойдет 1- lDx. В сделанных предположениях m точек попадает на отрезок длины l только в одном случае, когда в m отрезках попадает по одной точке. Тогда на основании 3-го свойства искомая вероятность равна
Точную вероятность получим путем предельного перехода при числе разделений отрезка
Тут мы разложили Найдем производящую функцию распределения Пуассона
Найти MX и DX
Вторая модель распределения Пуассона
Рассматривается обычная схема биноминального распределения, в котором n - велико, а p - достаточно мало. Тогда точная формула для вероятности появления события A в m испытаниях имеет вид
Эта формула при больших n вычисляется сложно. Такую вероятность заменяют приближенной
Для найденного a построим гипотетический ряд вероятностей
Предполагается, что для достаточно больших n и малых p искомая вероятность
является членом построенного гипотетического ряда вероятностей, а во вторых находится в малой окрестности предельного значения этого ряда. И, следовательно, это значение можно взять в качестве допустимой хорошей аппроксимации значений искомой вероятности. Непрерывные случайные величины. Будем рассматривать пространство элементарных событий как совокупность всех точек числовой оси. В этом случае введенная ранее функция распределения имеет вид: Пусть функция распределения является непрерывной. Найдем вероятность того, что в результате испытаний случайная величина X примет значение a, где a - произвольное действительное число. P(X=a). Рассмотрим неравенство: Доказать самим.
Следовательно:
Мы впервые столкнулись с ситуацией, когда событие принципиально может произойти в результате испытания, но имеет вероятность равную 0. В инженерном толковании это означает: в данной конечной серии испытаний данное событие никогда не произойдет. Случайная величина X называется непрерывной, если ее пространством элементарных событий является вся числовая ось (либо отрезок (отрезки) числовой оси), а вероятность наступления любого элементарного события равна нулю. P(a£X<b)=P(a£X£b)=F(b)-F(a) Если от сложного события вычесть конечное либо счетное множество, вероятность наступления нового события останется неизменной. Функция f(x) - числовая скалярная функция действительного аргумента x называется плотностью вероятности, и существует в точке x, если в этой точке существует предел:
Свойства плотности вероятности. 1. Плотность вероятности является неотрицательной функцией. 2.
3.
4.
Следствие: Если пространством элементарных событий является отрезок числовой оси, то пространство элементарных событий формально можно распространить на всю числовую ось, положив вне отрезка значение плотности вероятности равное 0. Второе эквивалентное определение плотности вероятности.
Пример: Равномерное распределение.
т.к.
Экспоненциальное распределение.
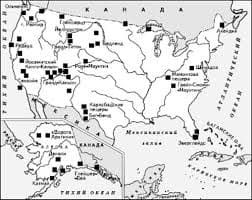 Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам... 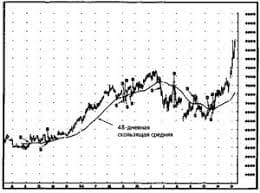 Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот...  Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор... 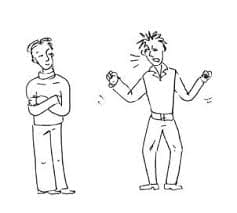 ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|