МОДЕЛИРОВАНИЕ СИСТЕМ УПРАВЛЕНИЯ

Методические указания к лабораторным работам

МОДЕЛИРОВАНИЕ СИСТЕМ УПРАВЛЕНИЯ: Методические указания к лабораторным работам / Сост.: В.Г.Баунин – Ковров: КГТА, 2007. – 60 с.

Методические указания разработаны в соответствии с требованиями ГОС к дисциплине «Моделирование систем управления» для специальности 2101.

Излагается теоретическое введение, порядок выполнения и основные требования к оформлению отчета по восьми лабораторным работам, проводимым на ПЭВМ с использованием программного пакета имитационного моделирования Matlab&Simulink.

Рецензент: канд. техн. наук, доцент Куренков В.П., (ФГУП «ВНИИ «Сигнал»).

Печатается по решению редакционно-издательского совета КГТА.

Государственное образовательное учреждение

«Ковровская государственная технологическая академия имени В.А.Дегтярева»

Методические указания к лабораторным работам

Изд. лиц. № 020354 от 05.06.97 г. Подписано в печать 19.06.007 г.

Формат 60х84/16. Бумага писчая № 1. Гарнитура «Таймс». Печать офсетная. Усл.-печ. л. 3,49. Уч.-изд.л. 3,45. Тираж 75 экз.

Государственное образовательное учреждение

«Ковровская государственная технологическая академия

Цель работы: ознакомление с блоками библиотеки пакета Simulink, используемыми при моделировании линейных непрерывных систем управления. Разработка машинной модели и исследование переходных процессов в двигателе постоянного тока независимого возбуждения.

Двигатели постоянного тока применяют в приводах, требующих плавного регулирования частоты вращения в широком диапазоне. По способу возбуждения различают двигатели с электромагнитным и магнитоэлектрическим возбуждением. Электрические двигатели с электромагнитным возбуждением делятся на двигатели с параллельным, последовательным, смешанным и независимым возбуждением.

Двигатели независимого возбуждения (см. рис.1) наиболее полно удовлетворяют основным требованиям, предъявляемым к исполнительным двигателям: отсутствие самохода (самоторможение двигателя при снятии сигнала управления); широкий диапазон регулирования частоты вращения; линейность механических и регулировочных характеристик; устойчивость работы во всем диапазоне частот вращения; большой пусковой момент; быстродействие; малые габариты и масса.

Составим дифференциальные уравнения, описывающие поведение двигателя независимого возбуждения при переходных процессах. Напряжение, подключенное к якорю двигателя, U уравновешивается ЭДС самоиндукции якоря, падением напряжения на активном сопротивлении якоря и противо-ЭДС, возникающей в якоре при вращении. Следовательно, для цепи якоря можно записать:

Дифференциальное уравнение моментов на валу двигателя имеет вид:

где J – момент инерции вращающихся частей, приведенный к валу двигателя;

M _с – статический момент или момент сопротивления (в общем случае равен сумме нагрузочного момента и момента трения двигателя).

Вращающий момент двигателя определяется по выражению:

В зависимости от размерности вращающего момента и угловой скорости (частоты вращения) количественная связь между этими коэффициентами имеет вид:

Математическая модель двигателя в виде структурной схемы, составленной по дифференциальным уравнениям, приведена на рис. 2.

Коэффициент момента c _м может быть определен из уравнения:

где M _ном – номинальный вращающий момент двигателя;

Сопротивление обмотки якоря двигателя определяется по уравнению:

ω_ном – номинальная скорость вращения двигателя, рад/с.

Индуктивность обмотки якоря может быть ориентировочно найдена по формуле [1]:

где с_х = 0,4 для машин без компенсационной обмотки; с_х = 0,1 для машин с компенсационной обмоткой; L _я – индуктивность обмотки якоря, Гн; р – число пар полюсов.

1. Рассчитать параметры математической модели двигателя постоянного тока для заданного преподавателем варианта исходных данных согласно табл. 1.

2. Ввести в ПЭВМ машинную модель двигателя постоянного тока с использованием блоков разделов Sources, Continuous, Math (Math Operations) и Sinks библиотеки пакета Simulink.

3. Исследовать переходные процессы в двигателе постоянного тока при скачкообразном изменении напряжения на якоре двигателя и при скачкообразном изменении момента нагрузки.

1. Математическую модель двигателя в виде структурной схемы.

3. Распечатку машинной модели, реализованной в пакете Simulink.

4. Графики переходных процессов тока якоря и скорости.

1. Схемы двигателей постоянного тока последовательного, параллельного, смешанного и независимого возбуждения. Принцип действия.

2. Уравнения движения двигателя постоянного тока.

3. Постройте на основе уравнений движения двигателя постоянного тока его математическую модель в виде структурной схемы.

4. Как рассчитываются параметры математической модели двигателя постоянного тока независимого возбуждения?

5. Какие размерности имеют параметры математической модели двигателя постоянного тока?

6. Какие блоки библиотеки пакета Simulink используются при моделировании двигателя постоянного тока независимого возбуждения? Какие параметры имеют эти блоки?

7. Объясните вид графиков изменения тока якоря и скорости вращения двигателя при скачкообразном изменении напряжения на якоре и при скачкообразном изменении момента нагрузки.

Цель работы: Исследование принципов автоматического регулирования, используемых при построении систем автоматического управления, на примере системы управления скоростью вращения исполнительного двигателя.

При построении систем автоматического управления могут быть использованы три фундаментальных принципа [5, 6]:

Сущность принципа разомкнутого регулирования (см. рис.1) состоит в том, что управляющее воздействие u на объект управления ОУ формируется управляющим устройством УУ только на основе входного воздействия x, вырабатываемого задающим устройством ЗУ, без использования сведений о возмущающем воздействии z и о регулируемой величине y. При этом регулирование выходной величины осуществляется с помощью задающего устройства, реализующего программу изменения входной величины x.

В систему регулирования, построенную по принципу регулирования по возмущению (см. рис. 2), введено компенсирующее устройство КУ, которое формирует дополнительное воздействие на устройство управления в зависимости от возмущающего воздействия z. В результате управляющее воздействие u позволяет компенсировать влияние z на изменение регулируемой величины y.

В системе регулирования, построенной по принципу регулирования по отклонению, управляющее воздействие u формируется в зависимости от отклонения управляемой величины y относительно заданного ее значения x. Наличие дополнительной цепи обратной связи по регулируемой величине образует замкнутую цепь прохождения сигналов или замкнутый контур управления. Поэтому данный принцип называют также принципом регулирования по замкнутому контуру. Математическая модель системы регулирования скорости вращения исполнительного двигателя, построенной по принципу разомкнутого регулирования, в виде структурной схемы представлена на рис. 4.

U _з – напряжение задания скорости вращения исполнительного двигателя, вырабатываемое задающим устройством;

K _у и Т _у – коэффициент передачи по напряжению и постоянная времени усилителя мощности;

U _m – максимальное выходное напряжение усилителя мощности;

R _я, L _я – сопротивление и индуктивность обмотки якоря двигателя;

M _с – момент сопротивления вращению двигателя;

J – момент инерции вращающихся частей, приведенный к валу двигателя;

Математическая модель системы регулирования скорости вращения исполнительного двигателя, построенной по принципу регулирования по отклонению, в виде структурной схемы представлена на рис. 5.

Как видно из рис. 5, в системе регулирования, построенной по принципу регулирования по отклонению, введена отрицательная обратная связь по скорости вращения исполнительного двигателя. Коэффициент передачи сигнала обратной связи на рис. 5 обозначен K _ос.

1. При выполнении лабораторной работы значения параметров математической модели двигателя постоянного тока независимого возбуждения принять равными рассчитанным для заданного преподавателем варианта исходных данных табл. 1 лабораторной работы № 1.

Значение напряжения задания скорости вращения исполнительного двигателя U _з принять равным 10 В.

Постоянную времени Т _у усилителя мощности принять равной 0,01 с.

2. Ввести в ПЭВМ машинную модель системы регулирования скорости вращения исполнительного двигателя, построенной по принципу разомкнутого регулирования, с использованием блоков разделов Sources, Continuous, Math (Math Operations), Sinks и блока Saturation раздела Nonlinear (Discontinuities) библиотеки пакета Simulink.

Коэффициент передачи по напряжению усилителя мощности K_у рассчитать по формуле:

где U _{дв ном} – номинальное напряжение двигателя.

3. Построить графики переходных процессов в системе регулирования скорости, построенной по принципу разомкнутого регулирования, при скачкообразном изменении напряжения задания скорости вращения исполнительного двигателя U _з на величину 10 В при моментах сопротивления движению M _с=0 и M _с= М _{дв ном}, где М _{дв ном} – номинальный момент двигателя. Значения М _{дв ном} приведены в таблице 1 лабораторной работы № 1.

Дать оценку отклонения установившейся скорости вращения исполнительного двигателя от его номинальной скорости вращения при разных значениях момента сопротивления движению.

4. Ввести в ПЭВМ машинную модель системы регулирования скорости вращения исполнительного двигателя, построенной по принципу регулирования по отклонению, с использованием блоков библиотеки пакета Simulink.

Коэффициент передачи сигнала обратной связи по скорости K _ос рассчитать по формуле:

где ω_ном – номинальная скорость вращения двигателя.

Значения ω_ном приведены в таблице 1 лабораторной работы № 1.

5. Проанализировать влияние величины коэффициента передачи K_у в системе по рис. 5 на качество переходного процесса при скачкообразном изменении U _з на величину 10В и отклонение установившейся скорости вращения ИД от его номинальной скорости вращения при M _с=0 и M _с= М _{дв ном}.

6. Провести сравнение точности поддержания номинальной скорости вращения исполнительного двигателя в системах по рис. 4, 5 при M _с=0 и M _с= М _{дв ном}.

1. Математические модели систем регулирования скорости вращения исполнительного двигателя, построенных по принципу разомкнутого регулирования и по принципу регулирования по отклонению.

2. Распечатки машинных моделей систем регулирования скорости вращения исполнительного двигателя, построенных по принципу разомкнутого регулирования и по принципу регулирования по отклонению, реализованных в пакете Simulink.

3. Графики переходных процессов в системах регулирования скорости вращения исполнительного двигателя по рис. 4 и рис. 5 (графики изменения скорости вращения и тока якоря).

4. Анализ влияния величины коэффициента передачи K _у в системе по рис. 5 на качество переходного процесса при скачкообразном изменении U _з и точность поддержания номинальной скорости вращения ИД при изменении M _с.

5. Сравнительный анализ точности регулирования скорости в системах по рис. 4 и 5.

1. Какие принципы регулирования ипользуются при построении систем автоматического регулирования и управления?

2. По каким показателям точности систем автоматического управления и качества переходного процесса Вы проводили сравнение систем регулирования скорости вращения исполнительного двигателя, построенных по принципу разомкнутого регулирования и по принципу регулирования по отклонению?

3. Выведете передаточные функции по управляющему (U _з) и возмущающему (M _с) воздействиям для систем регулирования скорости по рис. 4, 5. Дайте их анализ.

4. Какие блоки библиотеки пакета Simulink используются при моделировании систем регулирования скорости вращения исполнительного двигателя? Какие параметры имеют эти блоки?

5. Какие размерности имеют параметры математических моделей систем регулирования скорости вращения исполнительного двигателя?

6. Как влияет коэффициент передачи K _у в системе по рис. 5 на качество переходного процесса и точность системы регулирования?

системы управления с помощью инструмента Simulink LTI-Viewer

Цель работы: Ознакомление с инструментом Simulink LTI-Viewer. Исследование влияния параметров системы управления на запасы устойчивости и качество переходного процесса.

При решении задач анализа и синтеза систем управления широко используются методы, основанные на анализе их частотных характеристик.

По частотным характеристикам разомкнутой системы управления можно:

- определить запасы устойчивости и полосу пропускания системы;

- максимальное значение динамической ошибки системы при отработке задающего воздействия, изменяющегося по гармоническому закону;

- синтезировать корректирующие устройства, обеспечивающие требуемые динамические характеристики замкнутой системы управления и т.д.

Расчет и построение частотных характеристик системы управления в пакете Simulink выполняется с помощью инструмента LTI-Viewer [4].

Инструмент Simulink LTI-Viewer входит в состав пакета прикладных программ Control System Toolbox и предназначен для анализа линейных непрерывных систем. С помощью данного инструмента можно легко построить частотные характеристики исследуемой системы, а также получить графики переходных процессов при единичных ступенчатом и импульсном воздействиях, найти нули и полюса системы.

Для проведения исследования характеристик системы управления с использованием инструмента Simulink LTI-Viewer необходимо:

1. В меню окна Simulink-модели нажатием левой кнопки мыши выбрать Tools. В открывающемся меню Tools выбрать опцию Linear Analysis. При этом открывается окно Model_Inputs_and_Outputs как это показано на рис. 1, а также пустое окно Simulink LTI-Viewer.

Рис. 1. Исследуемая модель и окно Model_Inputs_and_Outputs инструмента Simulink

2. Установить блок Input Point на входе и блок Output Point на выходе исследуемой системы, как это показано на рис. 2.

3. В меню окна LTI Viewer выбрать команду Simulink и в выпадающем меню выбрать команду Get Linearized Model.

Данная команда выполняет линеаризацию модели и строит реакцию системы на единичное ступенчатое воздействие. Результат выполнения данного пункта показан на рис. 3.

Рис. 2. Исследуемая модель с установленными блоками Input Point и Output Point

Рис. 3. Реакция системы на единичное ступенчатое воздействие

4. Для получения других характеристик системы необходимо в меню окна LTI Viewer выбрать Edit и в выпадающем меню выбрать команду Plot Configuration. В результате выполнения этой команды откроется окно Plot Configuration, показанное на рис. 4.

В открывшемся окне можно выбрать число отображаемых графиков (панель Select a response plot configuration) и вид отображаемых графиков (панель Response type). Для построения доступны следующие графики (диаграммы):

· step – Реакция на единичное ступенчатое воздействие.

· impulse – Реакция на единичное импульсное воздействие.

· bode – Логарифмические амплитудная и фазовая частотные характеристики.

· bode mag – Логарифмическая амплитудная частотная характеристика.

На рис. 5 приведен пример окна Simulink LTI-Viewer с несколькими различными характеристиками исследуемой системы.

Рис. 5. Окно Simulink LTI-Viewer с несколькими графиками

Для настройки инструмента Simulink LTI-Viewer (установки или изменения единиц измерения, установки стиля графиков, установки интервалов времени и частот и т.д.) необходимо в меню окна LTI-Viewer выбрать Edit и в выпадающем меню выбрать команду Viewer Preferences.

С помощью данной команды выполняются следующие виды настройки:

1. Установка единиц измерения (вкладка Units). Вид окна при настройке единиц измерения показан на рис. 6.

Вкладка Units окна позволяет задать единицы измерения частоты (рад/c или Гц), уровня (dB или абсолютные единицы), фазы (градусы или радианы), а также установить вид шкалы частоты (логарифмический или линейный).

2. Установка стиля графиков (вкладка Style). На данной вкладке можно выполнить настройку шрифтов окна Simulink LTI-Viewer (панель Fonts), выбрать цвет осей графиков (панель Colors), а также задать нанесение линий сетки на графики (флажок Show grids). Внешний вид вкладки Style показан на рис. 7.

3. Установка параметров расчета переходного процесса (вкладка Characteristics). Данная вкладка позволяет задать параметры установленные "по умолчанию" для вычисления времени нарастания и времени переходного процесса. По умолчанию Simulink LTI-Viewer вычисляет время переходного процесса как время, когда переходная функция входит в 2% зону и больше не выходит из нее (параметр Show setting time within). Также можно изменить параметры для вычисления времени переходного процесса (Show rise time from). На данной вкладке имеется также флажок Unwrap phase, установка которого позволяет избежать отображения разрывов в фазо-частотной характеристике, связанных с областью определения функции arctg, вычисляющей фазовый сдвиг. Внешний вид вкладки Characteristics показан на рис. 8.

4. Установка интервалов времени и частоты (вкладка Parameters). На данной вкладке задается временной интервал для расчета переходного процесса (панель Time Vector), а также интервал частот для расчета частотных характеристик (панель Frequency Vector). Внешний вид вкладки Parameters показан на рис. 9.

1. Ввести в ПЭВМ машинную модель системы управления углом поворота по рис. 10 с использованием блоков библиотеки пакета Simulink для заданного преподавателем варианта исходных данных согласно табл. 1.

2. Для анализа частотных характеристик разомкнутой системы управления в машинной модели разомкнуть главную обратную связь. Построить логарифмические частотные характеристики некорректированной разомкнутой системы управления, приняв K ₁=1, T ₁= T ₂=0.

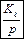
Рис. 10. Структурная схема системы управления:

α_з – заданный угол поворота; α – угол поворота объекта управления;

3. Исследовать влияние параметров K ₁, T ₁ и T ₂ последовательного корректирующего звена на такие характеристики системы управления как частота среза, запас устойчивости по фазе, запас устойчивости по амплитуде. Подобрать значения постоянных времени T ₁ и T ₂ последовательного корректирующего звена, обеспечивающие при достижении максимального для данной системы коэффициента передачи K ₁ запасы устойчивости по фазе не менее 30° и по амплитуде не менее 10 дБ.

4. Для исследования реакции замкнутой системы с выбранными значениями параметров последовательного корректирующего устройства на единичное ступенчатое воздействие, а также определения нулей и полюсов замкнутой системы в машинной модели замкнуть главную обратную связь. С помощью инструмента Simulink LTI-Viewer построить график переходного процесса при отработке входного единичного ступенчатого воздействия и диаграмму с расположением нулей и полюсов замкнутой системы управления с выбранными значениями параметров последовательного корректирующего устройства.

1. Математическую модель исследуемой системы управления в виде структурной схемы со значениями параметров, соответствующими заданному варианту.

2. Распечатку машинной модели системы управления.

3. Логарифмические частотные характеристики некорректированной и корректированной разомкнутых систем.

4. Анализ влияния параметров последовательного корректирующего звена на характеристики системы управления (частоту среза, запасы устойчивости по фазе и амплитуде).

5. Выбранные значения параметров последовательного корректирующего устройства.

6. График переходного процесса при отработке входного единичного ступенчатого воздействия и диаграмму с расположением нулей и полюсов передаточной функции замкнутой системы управления.

1. Какие характеристики системы управления могут быть исследованы с помощью инструмента Simulink LTI-Viewer?

2. Расскажите, как с помощью инструмента Simulink LTI-Viewer построить частотные характеристики системы управления, графики переходных процессов на ступенчатое или импульсное входное воздействие, определить нули и полюсы передаточной функции системы управления.

3. Как влияют параметры последовательного корректирующего звена на характеристики системы управления?

4. Сколько вещественных и комплексно-сопряженных нулей и полюсов имеет система управления с выбранными Вами значениями параметров последовательного корректирующего устройства? Покажите их расположение на диаграмме нулей и полюсов.

Цель работы: Разработка математической модели системы косвенной стабилизации, исследование точности и переходных процессов системы косвенной стабилизации на ЭВМ.

Эффективность использования различных измерительных устройств (ИУ) на подвижном основании существенно зависит от качки основания и от применяющихся средств стабилизации. Под ИУ имеются в виду установленные на подвижном объекте устройства, с помощью которых измеряются различные параметры (углы, линейные скорости, ускорения, перемещения, характеристики физических полей и др.) в инерциальной, земной или другой системах координат. К ним могут быть отнесены пеленгационные устройства, чувствительные элементы систем навигации, управления и другие устройства. Для уменьшения или полного устранения влияния качки на использование ИУ применяют различные методы стабилизации.

Сущность косвенного метода стабилизации [7] состоит в преобразовании угловых координат, характеризующих заданное положение ИУ в земной системе координат, в соответствующие угловые координаты (параметры стабилизации), отнесенные к системе координат, связанной с объектом, и во введении их в наведение ИУ. Решение задачи преобразования координат осуществляется с помощью преобразователей координат (ПК), на вход которых вводятся углы качки объекта, измеряемые гироскопическими устройствами. В ПК вводятся также заданные угловые координаты направления на ориентир в земной системе координат (см. рис. 1). ПК преобразует их в угловые координаты, отнесенные к системе координат, связанной с объектом. Последние называют также полными углами вертикального Ф и горизонтального Q наведения. Полные углы наведения вводятся в приводы ВН и ГН, которые разворачивают ИУ в заданном направлении и удерживают его при качке и рыскании объекта.

Рис. 1. Блок-схема системы косвенной стабилизации ИУ

Рассмотрим уравнения системы косвенной стабилизации ИУ в вертикальной плоскости при наличии продольной качки. Пусть в качестве силовой части привода стабилизации используются двигатель постоянного тока независимого возбуждения и транзисторный усилитель мощности. При составлении уравнений движения системы стабилизации будем считать механическую передачу, соединяющую ИУ и исполнительный двигатель привода стабилизации, абсолютно жесткой и безлюфтовой. С учетом этого допущения уравнение моментов, действующих относительно оси стабилизации, будет иметь вид:

J _д– момент инерции ротора исполнительного двигателя;

φ_иу – угол поворота ИУ относительно подвижного объекта;

i – передаточное число механической передачи (редуктора);

M _тр – момент сухого трения относительно оси стабилизации ИУ;

Момент двигателя M _д определяется по выражению:

Уравнение напряжений для цепи якоря двигателя:

T _я – электромагнитная постоянная времени двигателя;

Напряжение на якоре двигателя определяется по уравнениям:

где K _ум – коэффициент передачи усилителя мощности (УМ);

где W _кз – передаточная функция корректирующего звена;

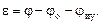
По уравнениям (1) – (6) составлена структурная схема системы стабилизации, приведенная на рис. 2.

Для повышения точности стабилизации ИУ при качке основания используется сигнал абсолютной скорости ИУ, измеряемый гироскопическим датчиком скорости. Структурная схема системы стабилизации с введением обратной связи по абсолютной скорости ИУ приведена на рис. 3.

Рис. 2. Структурная схема системы стабилизации

Рис. 3. Структурная схема системы стабилизации с обратной связью

Исследование точности и переходных процессов системы стабилизации проводится на персональных ЭВМ с использованием пакета Simulink, входящего в среду программных средств MATLAB.

1. Ввести в ПЭВМ машинную модель системы стабилизации по рис. 2с использованием блоков библиотеки пакета Simulink для заданного преподавателем варианта исходных данных согласно табл. 1. Принять W _кз= K _кз.

2. Подобрать значение коэффициента передачи K _кз, обеспечивающее:

- максимальное перерегулирование при отработке скачка входного воздействия φ=0,05 рад не более 30 %;

- максимальную динамическую ошибку при отработке продольной качки основания, изменяющейся по гармоническому закону φ_о=0,05 sin 5 t рад, не более 0,008 рад.

Построить графики переходных процессов в системе стабилизации по рис. 2 при отработке скачка входного воздействия φ=0,05 рад, а также при отработке продольной качки основания (графики изменения угла поворота φ_иу и ошибки ε) при выбранном значении коэффициента передачи K _кз.

3. Ввести в ПЭВМ машинную модель системы стабилизации по рис.3 с использованием блоков библиотеки пакета Simulink для заданного преподавателем варианта исходных данных согласно табл. 1. Принять W _кз= K _кз.

4. Подобрать значения коэффициентов передачи K _кз и K _гт, обеспечивающие:

- максимальное перерегулирование при отработке скачка входного воздействия φ=0,05 рад не более 10 %;

- максимальную динамическую ошибку при отработке продольной качки основания, изменяющейся по гармоническому закону φ_о=0,05 sin 5 t рад, не более 0,005 рад.

Построить графики переходных процессов в системе стабилизации по рис. 3 при отработке скачка входного воздействия φ=0,05 рад, а также при отработке продольной качки основания (графики изменения угла поворота φ_иу и ошибки ε) при выбранных значениях коэфф

ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между...

ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры...

Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот...

Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: