|
В) Перевод чисел в различные системы счисления
Операции над множествами
Объединением множеств A и B называется множество элементов, принадлежащих по крайней мере одному из данных множеств (т. е. либо A, либо B, либо одновременно и A и B). Обозначают 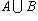 и читают "объединение A и B ". и читают "объединение A и B ".
Пересечением множеств A и B называется множество элементов, принадлежащих одновременно и A и B. Обозначают 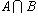 и читают "пересечение A и B ". и читают "пересечение A и B ".
Разностью множеств A и B называется множество элементов, принадлежащих A и не принадлежащих B. Обозначают A \ B и читают "разность A и B ".
Пример 1. Пусть A есть отрезок [1, 3], B - отрезок [2, 4]; тогда объединением 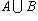 будет отрезок [1, 4], пересечением будет отрезок [1, 4], пересечением 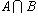 - отрезок [2, 3], разностью A \ B - полуинтервал [1, 2), B \ A - полуинтервал (3, 4]. - отрезок [2, 3], разностью A \ B - полуинтервал [1, 2), B \ A - полуинтервал (3, 4].
ИЛИ Пример 1
Пусть A = {1, 2, 3, 4, 5, 6, 7, 8, 9} и B = {1, 3, 5, 7, 9, 11, 13, 17, 19}.
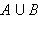 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 17, 19}, = {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 17, 19}, 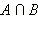 = {1, 3, 5, 7, 9}. = {1, 3, 5, 7, 9}.
Пример 2
Пусть A = [−2; 1] и B = (0; 3). Найти 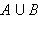 и и 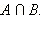
Решение
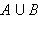 = [−2; 3), = [−2; 3), 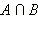 = (0; 1]. = (0; 1].
|
Пример 3
Пусть A = {1, 2, 3, 4, 5, 6, 7, 8, 9} и B = {1, 3, 5, 7, 9, 11, 13, 17, 19}. Найти A \ B и B \ A.
Решение
| A \ B = {2, 4, 6, 8}.
B \ A = {11, 13, 17, 19}.
| 1.2Доказать следующее тождество 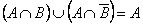 . .
Решение.
Докажем это тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна).
1. 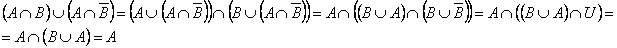
2. Построим соответствующие диаграммы Эйлера-Венна (рис. 7).
3.1
Таблица истинности
(p+q!)&(r!+s)
| p
| q
| r
| s
| !q
| pv(!q)
| !r
| (!r)vs
| (pv(!q))&((!r)vs)
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
При решении были использованы таблицы истинности следующих операций.
Операция ИЛИ — логическое сложение (дизъюнкция, объединение)
Операция И — логическое умножение (конъюнкция)
Операция НЕ — логическое отрицание (инверсия)
Совершенная дизъюнктивная нормальная форма формулы (СДНФ) это равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций, обладающая свойствами:
1. Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(x1,x2,...xn).
2. Все логические слагаемые формулы различны
3. Ни одно логическое слагаемое не содержит переменную и её отрицание
4. Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.
F = p ¯¯¯ q ¯¯ r ¯¯ s ¯¯¯+ p ¯¯¯ q ¯¯ r ¯¯ s + p ¯¯¯ q ¯¯ rs + pq ¯¯ r ¯¯ s ¯¯¯+ pq ¯¯ r ¯¯ s + pq ¯¯ rs + pqr ¯¯ s ¯¯¯+ pqr ¯¯ s + pqrs
Совершенная конъюнктивная нормальная форма формулы (СКНФ) это равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций, удовлетворяющая свойствам:
1. Все элементарные дизъюнкции содержат все переменные, входящие в функцию F(x1,x2,...xn)
2. Все элементарные дизъюнкции различны
3. Каждая элементарная дизъюнкция содержит переменную один раз
4. Ни одна элементарная дизъюнкция не содержит переменную и её отрицание
F =(p + q + r ¯¯+ s)(p + q ¯¯+ r + s)(p + q ¯¯+ r + s ¯¯¯)(p + q ¯¯+ r ¯¯+ s)(p + q ¯¯+ r ¯¯+ s ¯¯¯)(p ¯¯¯+ q + r ¯¯+ s)(p ¯¯¯+ q ¯¯+ r ¯¯+ s)
Метод диаграмм Вейча.
Метод позволяет быстро получать минимальные ДНФ булевой функции f небольшого числа переменных. В основе метода лежит задание булевых функций диаграммами некоторого специального вида, получившими название диаграмм Вейча.
| | | r
| r
| !r
| !r
| | | | !s
| s
| s
| !s
| | p
| !q
|
|
|
|
| | p
| q
|
|
|
|
| | !p
| q
|
|
|
|
| | !p
| !q
|
|
|
|
|
3.2
Составлю таблицу истинности!
Три ученика из разных школ на вопрос, в какой школе учатся, ответили:
Артем: я учусь в школе №534, а Кирилл - в школе №76
Кирилл: я учусь в школе №534, а Артем - в школе №105
Максим:я учусь в школе № 534, а Артем - в школе №76
Каждый из них сказал правду и один из раз солгал. В каких школах учатся Артем, Кирилл, Максим?
- №534 №76 №105
Артем - - +
Кирилл - + -
Максим + - - - Надо нарисовать таблицу; по горизонтали строки Арт, Кир и Макс; по вертикали столбцы 534, 76 и 105. В таблице отметить крестиками ответы. Получим, что всего один крестик у максима - это 534. Значит Максим учится в 534. Кириллу остается 76, т.к. он не может учиться в 534, а других выборов нет. А Артему достается 105.
№5Перевод чисел в различные системы счисления
Делим число на 2 и выписываем остатки
306 = 153·2 + 0
153 = 76·2 + 1
76 = 38·2 + 0
38 = 19·2 + 0
19 = 9·2 + 1
9 = 4·2 + 1
4 = 2·2 + 0
2 = 1·2 + 0
Последний множитель перед 2 равный 1 записываем первым.
Затем записываем найденные остатки в обратном порядке.
Получаем: 100110010
Делим число на 8 и выписываем остатки
306 = 38·8 + 2
38 = 4·8 + 6
Последний множитель перед 8 равный 4 записываем первым.
Затем записываем найденные остатки в обратном порядке.
Получаем: 462
Делим число на 16 и выписываем остатки
306 = 19·16 + 2
19 = 1·16 + 3
Последний множитель перед 16 равный 1 записываем первым.
Затем записываем найденные остатки в обратном порядке.
Получаем: 132
Б) Делим число на 2 и выписываем остатки
467 = 233·2 + 1
233 = 116·2 + 1
116 = 58·2 + 0
58 = 29·2 + 0
29 = 14·2 + 1
14 = 7·2 + 0
7 = 3·2 + 1
3 = 1·2 + 1
Последний множитель перед 2 равный 1 записываем первым.
Затем записываем найденные остатки в обратном порядке.
Получаем: 111010011
Делим число на 8 и выписываем остатки
467 = 58·8 + 3
58 = 7·8 + 2
Последний множитель перед 8 равный 7 записываем первым.
Затем записываем найденные остатки в обратном порядке.
Получаем: 723
Делим число на 16 и выписываем остатки
467 = 29·16 + 3
29 = 1·16 + 13 (13 записывается как D)
Последний множитель перед 16 равный 1 записываем первым.
Затем записываем найденные остатки в обратном порядке.
Получаем: 1D3
Операции над множествами
Объединением множеств A и B называется множество элементов, принадлежащих по крайней мере одному из данных множеств (т. е. либо A, либо B, либо одновременно и A и B). Обозначают 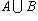 и читают "объединение A и B ". и читают "объединение A и B ".
Пересечением множеств A и B называется множество элементов, принадлежащих одновременно и A и B. Обозначают 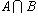 и читают "пересечение A и B ". и читают "пересечение A и B ".
Разностью множеств A и B называется множество элементов, принадлежащих A и не принадлежащих B. Обозначают A \ B и читают "разность A и B ".
Пример 1. Пусть A есть отрезок [1, 3], B - отрезок [2, 4]; тогда объединением 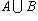 будет отрезок [1, 4], пересечением будет отрезок [1, 4], пересечением 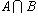 - отрезок [2, 3], разностью A \ B - полуинтервал [1, 2), B \ A - полуинтервал (3, 4]. - отрезок [2, 3], разностью A \ B - полуинтервал [1, 2), B \ A - полуинтервал (3, 4].
ИЛИ Пример 1
Пусть A = {1, 2, 3, 4, 5, 6, 7, 8, 9} и B = {1, 3, 5, 7, 9, 11, 13, 17, 19}.
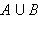 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 17, 19}, = {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 17, 19}, 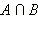 = {1, 3, 5, 7, 9}. = {1, 3, 5, 7, 9}.
Пример 2
Пусть A = [−2; 1] и B = (0; 3). Найти 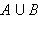 и и 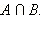
Решение
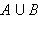 = [−2; 3), = [−2; 3), 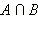 = (0; 1]. = (0; 1].
|
Пример 3
Пусть A = {1, 2, 3, 4, 5, 6, 7, 8, 9} и B = {1, 3, 5, 7, 9, 11, 13, 17, 19}. Найти A \ B и B \ A.
Решение
| A \ B = {2, 4, 6, 8}.
B \ A = {11, 13, 17, 19}.
| 1.2Доказать следующее тождество 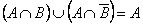 . .
Решение.
Докажем это тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна).
1. 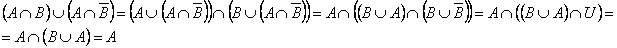
2. Построим соответствующие диаграммы Эйлера-Венна (рис. 7).
 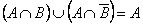
3.1
Таблица истинности
(p+q!)&(r!+s)
| p
| q
| r
| s
| !q
| pv(!q)
| !r
| (!r)vs
| (pv(!q))&((!r)vs)
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
При решении были использованы таблицы истинности следующих операций.
Операция ИЛИ — логическое сложение (дизъюнкция, объединение)
Операция И — логическое умножение (конъюнкция)
Операция НЕ — логическое отрицание (инверсия)
Совершенная дизъюнктивная нормальная форма формулы (СДНФ) это равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций, обладающая свойствами:
1. Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(x1,x2,...xn).
2. Все логические слагаемые формулы различны
3. Ни одно логическое слагаемое не содержит переменную и её отрицание
4. Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.
F = p ¯¯¯ q ¯¯ r ¯¯ s ¯¯¯+ p ¯¯¯ q ¯¯ r ¯¯ s + p ¯¯¯ q ¯¯ rs + pq ¯¯ r ¯¯ s ¯¯¯+ pq ¯¯ r ¯¯ s + pq ¯¯ rs + pqr ¯¯ s ¯¯¯+ pqr ¯¯ s + pqrs
Совершенная конъюнктивная нормальная форма формулы (СКНФ) это равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций, удовлетворяющая свойствам:
1. Все элементарные дизъюнкции содержат все переменные, входящие в функцию F(x1,x2,...xn)
2. Все элементарные дизъюнкции различны
3. Каждая элементарная дизъюнкция содержит переменную один раз
4. Ни одна элементарная дизъюнкция не содержит переменную и её отрицание
F =(p + q + r ¯¯+ s)(p + q ¯¯+ r + s)(p + q ¯¯+ r + s ¯¯¯)(p + q ¯¯+ r ¯¯+ s)(p + q ¯¯+ r ¯¯+ s ¯¯¯)(p ¯¯¯+ q + r ¯¯+ s)(p ¯¯¯+ q ¯¯+ r ¯¯+ s)
Метод диаграмм Вейча.
Метод позволяет быстро получать минимальные ДНФ булевой функции f небольшого числа переменных. В основе метода лежит задание булевых функций диаграммами некоторого специального вида, получившими название диаграмм Вейча.
| | | r
| r
| !r
| !r
| | | | !s
| s
| s
| !s
| | p
| !q
|
|
|
|
| | p
| q
|
|
|
|
| | !p
| q
|
|
|
|
| | !p
| !q
|
|
|
|
|
3.2
Составлю таблицу истинности!
Три ученика из разных школ на вопрос, в какой школе учатся, ответили:
Артем: я учусь в школе №534, а Кирилл - в школе №76
Кирилл: я учусь в школе №534, а Артем - в школе №105
Максим:я учусь в школе № 534, а Артем - в школе №76
Каждый из них сказал правду и один из раз солгал. В каких школах учатся Артем, Кирилл, Максим?
- №534 №76 №105
Артем - - +
Кирилл - + -
Максим + - - - Надо нарисовать таблицу; по горизонтали строки Арт, Кир и Макс; по вертикали столбцы 534, 76 и 105. В таблице отметить крестиками ответы. Получим, что всего один крестик у максима - это 534. Значит Максим учится в 534. Кириллу остается 76, т.к. он не может учиться в 534, а других выборов нет. А Артему достается 105.
№5Перевод чисел в различные системы счисления
Делим число на 2 и выписываем остатки
306 = 153·2 + 0
153 = 76·2 + 1
76 = 38·2 + 0
38 = 19·2 + 0
19 = 9·2 + 1
9 = 4·2 + 1
4 = 2·2 + 0
2 = 1·2 + 0
Последний множитель перед 2 равный 1 записываем первым.
Затем записываем найденные остатки в обратном порядке.
Получаем: 100110010
Делим число на 8 и выписываем остатки
306 = 38·8 + 2
38 = 4·8 + 6
Последний множитель перед 8 равный 4 записываем первым.
Затем записываем найденные остатки в обратном порядке.
Получаем: 462
Делим число на 16 и выписываем остатки
306 = 19·16 + 2
19 = 1·16 + 3
Последний множитель перед 16 равный 1 записываем первым.
Затем записываем найденные остатки в обратном порядке.
Получаем: 132
Б) Делим число на 2 и выписываем остатки
467 = 233·2 + 1
233 = 116·2 + 1
116 = 58·2 + 0
58 = 29·2 + 0
29 = 14·2 + 1
14 = 7·2 + 0
7 = 3·2 + 1
3 = 1·2 + 1
Последний множитель перед 2 равный 1 записываем первым.
Затем записываем найденные остатки в обратном порядке.
Получаем: 111010011
Делим число на 8 и выписываем остатки
467 = 58·8 + 3
58 = 7·8 + 2
Последний множитель перед 8 равный 7 записываем первым.
Затем записываем найденные остатки в обратном порядке.
Получаем: 723
Делим число на 16 и выписываем остатки
467 = 29·16 + 3
29 = 1·16 + 13 (13 записывается как D)
Последний множитель перед 16 равный 1 записываем первым.
Затем записываем найденные остатки в обратном порядке.
Получаем: 1D3
В) Перевод чисел в различные системы счисления
| Целая часть от деления
| Остаток от деления
| | 218 div 2 = 109
| 218 mod 2 = 0
| | 109 div 2 = 54
| 109 mod 2 = 1
| | 54 div 2 = 27
| 54 mod 2 = 0
| | 27 div 2 = 13
| 27 mod 2 = 1
| | 13 div 2 = 6
| 13 mod 2 = 1
| | 6 div 2 = 3
| 6 mod 2 = 0
| | 3 div 2 = 1
| 3 mod 2 = 1
| | 1 div 2 = 0
| 1 mod 2 = 1
| Остаток от деления записываем в обратном порядке. Получаем число в 2-ой системе счисления: 11011010
218 = 110110102
Для перевода дробной части числа последовательно умножаем дробную часть на основание 2. В результате каждый раз записываем целую часть произведения.
0.5*2 = 1 (целая часть 1)
0*2 = 0 (целая часть 0)
0*2 = 0 (целая часть 0)
0*2 = 0 (целая часть 0)
Получаем число в 2-ой системе счисления: 1000
0.5 = 10002
В итоге получаем число: 11011010.10002
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




