Достаточные условия существования локальных экстремумов
Пусть функция  непрерывна в непрерывна в  и существуют конечные или бесконечные односторонние производные и существуют конечные или бесконечные односторонние производные  . Тогда при условии . Тогда при условии

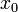 является точкой строгого локального максимума. А если является точкой строгого локального максимума. А если

то 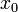 является точкой строгого локального минимума. является точкой строгого локального минимума.
Заметим, что при этом функция не дифференцируема в точке 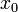
Пусть функция  непрерывна и дважды дифференцируема в точке непрерывна и дважды дифференцируема в точке 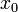 . Тогда при условии . Тогда при условии
 и и 
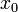 является точкой локального максимума. А если является точкой локального максимума. А если
 и и 
то 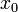 является точкой локального минимума. является точкой локального минимума.
Пусть функция  дифференцируема дифференцируема  раз в точке раз в точке 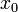 и и  , а , а  . .
14. Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.
Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.
Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.
 Точка Точка  называется точкой перегиба графика функции y = f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки называется точкой перегиба графика функции y = f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки  , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости. , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.
Другими словами, точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее.
Если необходимо, обратитесь к разделу касательная к графику функции в точке, чтобы вспомнить условия существования невертикальной и вертикальной касательной.
На рисунке ниже представлены несколько примеров точек перегиба (отмечены красными точками). Заметим, что некоторые функции могут не иметь точек перегиба, а другие могут иметь одну, несколько или бесконечно много точек перегиба.

15. Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.
Определение 7.1 Вертикальной асимптотой графика функции  называется вертикальная прямая называется вертикальная прямая  , если , если  или или  при каком-либо из условий: при каком-либо из условий:  , ,  , ,  . Заметим, что мы при этом не требуем, чтобы точка . Заметим, что мы при этом не требуем, чтобы точка  принадлежала области определения функции принадлежала области определения функции 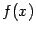 , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки:  или или  , где , где  . .
Определение 7.2 Наклонной асимптотой графика функции  при при  называется прямая называется прямая  , если выполнены два условия: , если выполнены два условия:
1) некоторый луч  целиком содержится в целиком содержится в  ; ;
2) расстояние по вертикали между графиком и прямой стремится к 0 при  : :

| (7.1)
|
Наклонной асимптотой графика функции  при при 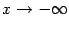 называется прямая называется прямая  , если , если
1) некоторый луч  целиком содержится в целиком содержится в  ; ;
2) расстояние по вертикали между графиком и прямой стремится к 0 при 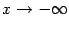 : :


Рис.7.6.Графики функций, имеющие наклонные асимптоты при  и при и при 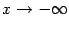
В случае, если наклонная асимптота расположена горизонтально, то есть при  , она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямая , она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямая  является горизонтальной асимптотой графика является горизонтальной асимптотой графика  при при  или или 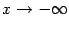 , если , если

Или  соответственно. соответственно.
Определение первообразной.
Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство  для любого х из заданного промежутка.Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо для любого х из заданного промежутка.Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо
равенство  . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину. . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
Определение неопределенного интеграла. Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается  . .
На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).
1. 
Производная результата интегрирования равна подынтегральной функции.
2. 
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.
3.  , где k – произвольная константа. , где k – произвольная константа.
Коэффициент можно выносить за знак неопределенного интеграла.
4. 
Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




