ПОЛЕЗНОЕ

Как развить коммуникабельность Почему могут возникнуть ссоры между супругами, в то время как их отношения кажутся прочными Почему появляется страх? Как стать богатым и отойти от дел молодым Советы от доктора Айболита «Как быть здоровым» Как сделать приглашение правильно Точка зрения. Как сделать сотрудника вовлеченным? Лень и как с ней бороться. Психологические аспекты Способов заработать с помощью internet Лекции по Основам предпринимательства Последнее добавление

КАТЕГОРИИ

Основні поняття про функції багатьох змінних

Стр 1 из 2Следующая ⇒

Основні поняття про функції багатьох змінних

Вивчення зв’язків і закономірностей, які існують в матеріальному світі, часто приводять до функції не однієї, а багатьох змінних. Ці функції дозволяють виражати більш складні залежності, ніж функції однієї змінної. Тому теорія функцій багатьох змінних має широке практичне застосування в різних галузях.

1.1. Означення функції багатьох змінних.

Функція двох змінних та її графічне зображення

Змінні називаються незалежними між собою, якщо кожна із них може приймати довільні значення в своїй області зміни незалежно від того, які значення приймають при цьому інші змінні.

Означення 1. Функцією багатьох змінних називається така закономірність, при якій змінним із деякої множини ставиться у відповідність одне значення із множини .

Наприклад:

Множина називається областю визначення функції

а множина - область значень цієї функції. Наприклад, функція задана для всіх і , для яких виконується нерівність У даному випадку областю визначення функції є круг на площині з центром в точці і радіусом R=3 Область значень цієї функції .

Частинним випадком функції багатьох змінних є функція двох змінних для якої можна дати поняття графіка функції. В загальному випадку графіком такої функції є поверхня у трьохвимірному просторі R³

Приклад 1. Графіком цієї функції є параболоїд обертання (мал.1).

1.2. Економічні задачі, що приводять до поняття функцій багатьох змінних

Приведемо приклади конкретних функцій багатьох змінних, які зустрічаються в економічних задачах.

Приклад 2. Нехай підприємство випускає тільки один товар і на його випуск затрачається тільки одна сировина (один ресурс). Підприємство характеризується повністю своєю виробничою функцією y=f(x) залежність об’єму випущеного товару від об’єму затраченої сировини Така виробнича функція називається одноресурсною.

Якщо на виробництво продукції певного типу витрачається багато видів сировини (ресурсів) х₁, х₂,...,х_n то така виробнича функція називається багаторесурсною або багатофакторною:

Найбільш відомою виробничою функцією є функція

Кобба - Дугласа , де - невід’ємні константи, причому ;

K - об’єм фондів в вартісному або натуральному вираженні;

L - об’єм трудових ресурсів – число працівників, число

людино-днів;

y - випуск продукції в вартісному або натуральному виразі. На цьому прикладі видно, що функція Кобба-Дугласа є функцією двох незалежних змінних K і L.

Приклад 3. Розглянемо основне рівняння класичної кількісної теорії грошей, яке називається рівнянням обміну Фішера:

MV=PY

даному рівнянні будь-яка із змінних M,V,P,Y може розглядатися як функція трьох змінних, де

M - це загальна кількість грошей, наявних в обороті;

V - швидкість їх обороту (скільки раз кожна гривня

бере участь в розрахунках в середньому за рік);

Y - національний продукт або дохід (національний продукт

– це всі готові товари і послуги, що виготовлені в економічній

системі у вартісному виразі; національний дохід – це всі виплати,

одержані домашніми господарствами: заробітна плата, рента, прибуток; національний продукт і національний дохід чисельно рівні);

- рівень цін (середнє зважене значення цін готових товарів і послуг, що визначені відносно базового показника, прийнятого за одиницю).

Нехай - тобто ціна є функцією трьох незалежних змінних. Тоді із збільшенням грошової маси (кількості грошей) в декілька разів (тобто гроші просто надрукують), ціни зростуть в стільки ж разів, при умові, що інші величини і залишаться незмінними. Такі дії і є найчастіше причиною інфляції.

Лінії та поверхні рівня. Гіперповерхні рівня

Поверхні другого порядку

Найбільш вивчені поверхні в курсі аналітичної геометрії – поверхні другого порядку. В загальному випадку рівняння такої поверхні має вигляд.

Залежно від значень коефіцієнтів одержують різні поверхні другого порядку.

Наприклад:

- конус;

- напівсфера;

3) -

еліптичний параболоїд;

-гіперболічний параболоїд;

-трьохосний

еліпсоїд.

Для вивчення поверхонь в трьохвимірному просторі застосовується метод перерізів. Суть цього методу така: перерізаємо задану поверхню площинами. В результаті отримуємо деякі криві, які характеризують поверхню.

Приклад 3. Нехай Отримаємо рівняння (рівняння кола). Покладемо тоді - рівняння параболи в площині , яка зміщена на одиниць вверх по осі . Покладемо Отримаємо рівняння Одержали рівняння параболи в площині , яка зміщена на одиниць вверх по осі З цих досліджень випливає, що графіком функції є параболоїд обертання навколо осі

Гіперповерхня рівня

Нехай задана функція від змінних Якщо покласти то одержимо рівняння яке називається рівнянням гіперповерхні рівня в просторі . Наприклад: Якщо то рівняння є рівнянням гіперсфери в з центром в точці і радіусом .

Функції двох змінних

Похідна складної функції

Відомо, що для похідної складної функції однієї змінної де має місце формула

Узагальнимо цю формулу на випадок функції двох змінних Нехай задана диференційовна функція , яка має неперервні частинні похідні і . Допустимо, що аргументи і є в свою чергу диференційовними функціями від третьої змінної Ясно, що функція є складною функцією від змінної : .

Знайдемо похідну цієї функції по змінній . Для цього надамо приросту аргументу і знайдемо повний приріст функції , якщо аргументи і набувають відповідно приростів і :

Перепишемо цей приріст в іншому вигляді:

Застосуємо тепер теорему Лагранжа про скінчені прирости відповідно до першої і другої квадратних дужок. Тоді отримаємо:

Допустимо тепер, що частинні похідні неперервні по сукупності змінних і , тоді:

Таким чином,

Тепер згідно означення похідної знаходимо:

Перейшовши до границі при і враховуючи, що , отримаємо формулу:

Ця похідна називається повною похідною функції по аргументу . Аналогічно вводиться формула повної похідної для функції

де .

Поняття похідної функції можна узагальнити, якщо ввести похідну функції по напрямку.

Похідна функції по напрямку

Нехай функція задана в деякій замкнутій області площини .

Нехай в цій області задана точка . Надамо приросту аргументам відповідно і , тоді отримаємо точку . Розглянемо вектор .

Позначимо через кут, який утворює вектор з віссю , а через - довжину цього вектора. Тоді можна записати:

або

Таким чином: Значення функції

в точках і відповідно будуть такі:

і .

Звідси випливає, що коли зафіксувати точку і напрямок вектора і міняти тільки , то функцію можна записати у вигляді , а її значення в точках і

відповідно і Таким чином

Згідно означення похідної функції однієї змінної, похідна функції по змінній дорівнює

Цю границю назвемо похідною функції по даному напрямку. Виходячи із викладеного вище, функцію можна вважати складною функцією по . Її повна похідна по дорівнює

Але , тому

Цю формулу можна узагальнити на випадок функції трьох змінних . В цьому випадку напрямок задається вектором і формула диференціювання по напрямку відповідно матиме вид

Встановимо зв’язок між похідною функції по напрямку і градієнтом цієї функції. Для цього розглянемо вектори

і .

Помножимо скалярно вектор на вектор , отримаємо:

. Таким чином,

. Згідно з означенням скалярного добутку .

Із цієї формули випливає, що у випадку, коли напрямок вектора співпадає з напрямком вектора

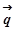Висновок. Похідна функції z=f(x,y) має найбільше значення по напрямку градієнта

і дорівнює модулю градієнта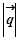

Приклад 3. Обчислити градієнт функції в точці M₀(3,4).

Розв’язування. Знаходимо частинні похідні функції

;

Обчислимо їх значення в даній точці:

; .

Таким чином

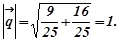
Багатьох змінних

Нехай z=f(x,y) - функція двох змінних. Надамо обом змінним прирости відповідно Δ x і Δ y, тоді функція z отримає приріст який називається повним приростом функції.

Відомо, що для функції y= φ (x), яка має похідну , приріст функції можна зобразити у вигляді

(5.8)

де ε→ 0, якщо Δ x→0.

Тоді головна лінійна частина приросту функції називається диференціалом функції dy=φ′(x) Δ x= φ′(x)dx.

В випадку функції двох або більше змінних наявність частинних похідних ще не гарантує того, що повний приріст функції

можна представити в виді, аналогічному (5.8).

Означення 6. Функція z=f(x,y) називається диференційовною в даній точці якщо її повний приріст в цій точці можна представити в виді:

(5.9)

де при а і не залежать відприростів

Доданки і є, очевидно, нескінченно малими величинами вищого порядку малості, ніж і

Означення 7. Повним диференціалом функції називається головна лінійна частина приросту функції відносно і , тобто: або

ТЕОРЕМА 1. Якщо функція диференційовна в даній точці , то існують частинні похідні цієї функції і має місце рівність тобто

. (5.10)

Доведення. Нехай функція диференційовна. Тоді має місце формула (5.9). Покладемо тоді із (5.9) отримаємо

звідки , де якщо

Оскільки - стала величина ( і фіксовані), то

Аналогічно доводиться, що Таким чином, формула (5.10) доведена.

Нехай задана функція Можна довести, по аналогії з функцією що в випадку диференційовності функції має місце формула

(5.11)

Навпаки, якщо допустити, що функція має частинні похідні, які є неперервними функціями по сукупності змінних в околі точки M(x₁,x₂,…,x_n) то справедлива формула (5.11).