|
|
Економічний зміст частинних похідних ⇐ ПредыдущаяСтр 2 из 2 Відповідним чином можна надати економічного змісту частинним похідним. Розглянемо в якості прикладу функцію Кобба-Дугласа Величину Величину Величину Зафіксуємо біжучий стан підприємства, тобто об’єм фондів
А це є частковий приріст функції по Оскільки Отже, частинна похідна від виробничої функції по об’єму трудових ресурсів приблизно рівна додатковій вартості продукції, що вироблена ще одним робітником. Тому похідна
називається граничною продуктивністю праці. Якщо ж збільшити фонди ще на одиницю – купити ще один верстат, то додаткова вартість продукції, що вироблена на ньому, приблизно дорівнює частинній похідній виробничої функції по об’єму фондів. Тоді
І гранична продуктивність праці, і гранична фондовіддача – це абсолютні величини. Але в економіці надзвичайно цікаво знати на скільки відсотків зміниться випуск продукції, якщо число робітників збільшиться на 1%, або якщо фонди зростуть на 1%. Тому розглядаються поняття еластичності випуску продукції по об’єму трудових ресурсів і еластичності випуску продукції по фондах:
Звідси маємо економічний зміст параметрів функції Кобба-Дугласа.
Приклад 2. Нехай виробнича функція є функцією Кобба-Дугласа. Щоб збільшити випуск продукції на 5% треба збільшити фонди на 10% або чисельність робітників на 15%. В 2001 році один робітник виготовляв продукцію на 2000 грн., а всього робітників 1000. Основні фонди оцінювались в 4 млн.грн. Записати виробничу функцію, величину середньої фондовіддачі і середньої продуктивності праці. Розв’язування. Зрозуміло, що еластичність випуску продукції по праці
Отже, виробнича функція
Частинні похідні функції багатьох змінних Ми розглянули випадок функції двох змінних. Для функції
Очевидно, що для функцій багатьох змінних можна використовувати відомі правила диференціювання, включаючи таблиці похідних, які отримані для функцій однієї змінної.
§5. Градієнт функції багатьох змінних. Похідна функції по напрямку
5.1. Градієнт функції багатьох змінних Означення 5. Градієнтом функції
Аналогічно для функції
Відповідно вводимо градієнт функції
Скорочено градієнт функції позначимо через
Похідна складної функції Відомо, що для похідної складної функції однієї змінної
Узагальнимо цю формулу на випадок функції двох змінних Знайдемо похідну цієї функції по змінній
Перепишемо цей приріст в іншому вигляді:
Застосуємо тепер теорему Лагранжа про скінчені прирости відповідно до першої і другої квадратних дужок. Тоді отримаємо:
Допустимо тепер, що частинні похідні неперервні по сукупності змінних
Таким чином,
Тепер згідно означення похідної знаходимо:
Перейшовши до границі при
Ця похідна називається повною похідною функції
де Поняття похідної функції
Похідна функції по напрямку Нехай функція Нехай в цій області задана точка Позначимо через
Таким чином:
Звідси випливає, що коли зафіксувати точку відповідно
Згідно означення похідної функції однієї змінної, похідна функції
Цю границю назвемо похідною функції
Але Цю формулу можна узагальнити на випадок функції трьох змінних
Встановимо зв’язок між похідною функції
Помножимо скалярно вектор
Із цієї формули випливає, що у випадку, коли напрямок вектора
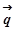 і дорівнює модулю градієнта і дорівнює модулю градієнта 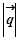 . .
Приклад 3. Обчислити градієнт функції Розв’язування. Знаходимо частинні похідні функції
Обчислимо їх значення в даній точці:
  Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам...  ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между...  Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем...  Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|