|
|
Линеаризация статических характеристик звеньев ⇐ ПредыдущаяСтр 3 из 3 Статическая характеристика звена описывает соотношение между входной и выходной величинами в статике (установившемся режиме). Статические характеристики могут быть заданы графически и аналитически. При наличии статических характеристик звеньев можно построить статические характеристики группы звеньев, а также характеристики всей системы. Замена реальных нелинейных характеристик линейными называется линеаризацией. Пусть имеем нелинейное звено (рис. 1.17).
Рис. 1.17 Рис. 1.18 Статическая характеристика звена описывается функцией
Если функция в окрестности x 01 непрерывна и дифференцируема, то ее можно разложить в ряд Тейлора
Через Обычно считают, что члены высшего порядка малости много меньше двух первых слагаемых, потому ими пренебрегают
Вычтем из (2.3) уравнение (2.1) почленно и получим
 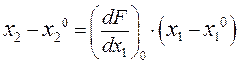 или или
где Уравнение (2.4) называется уравнением в отклонениях и соответствует статике звена. Практически линеаризацию проводят чаще всего путем проведения касательной в точке установившегося режима и определяют Линеаризация нелинейных дифференциальных уравнений. Чаще всего процессы в звеньях описываются нелинейными дифференциальными уравнениями. Рассмотрим процесс линеаризации на примере дифференциального уравнения второго порядка
где Пусть в установившемся режиме звена справедливо
Тогда уравнение установившегося режима примет вид
Разложим (2.5) в ряд Тейлора в точке установившегося режима, рассматривая (2.5) как функцию от независимых переменных,
где Вычтем из (2.7) уравнение (2.6) и положим Q =0, тогда получим уравнение в отклонениях:
где
Уравнение (2.8) описывает тот же процесс, что и (2.5), но имеет отличия: · Уравнение (2.8) является линейным относительно переменных · Вместо · Уравнение (2.8) является приближенным. Безразмерная форма записи уравнений Введем относительные переменные:
Подставим (2.9) в (2.8)
Разделим (2.10) на
Уравнение (2.11) можно преобразовать
где
Решая уравнение (2.12) как линейное, можно получить закон изменения выходной величины Пример линеаризации звена. Дана нелинейная функция Образуем функцию Разложим функцию в ряд Тейлора
Откуда получим уравнение в отклонениях
ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ СИСТЕМЫ Динамическое звено – это устройство любого вида и принципа действия, описываемое определенным дифференциальным уравнением. Свойства звена могут быть определены различными характеристиками: передаточной функцией, временными характеристиками и частотными характеристиками. Передаточная функция звена Пусть дано динамическое звено.
Дифференциальное уравнение такого звена можно записать следующим образом:
Применим преобразование Лапласа, тогда уравнение (3.1) можно записать:
Правила преобразования Лапласа для производных: Если
Тогда в уравнении (3.2)
Из уравнения (3.2) выразим
Первая составляющая представляет собой эффект действия входного сигнала на звено. Вторая составляющая учитывает начальные условия входной и выходной величин. Пусть при
Тогда
или
Выражение (3.5) называется передаточной функцией звена. Таким образом, передаточной функцией звена (или системы) называется отношение изображений выходной и входной величин при нулевых начальных условиях. С физической точки зрения Выражение (3.5) можно представить графически (рис. 3.2).
  ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры...  Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...  Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот...  Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|