Тема 2: Коэффициент корреляции
Коэффициент корреляции  характеризует степень тесноты линейной зависимости между случайными величинами характеризует степень тесноты линейной зависимости между случайными величинами  и и  и он вычисляется по формуле: и он вычисляется по формуле:
 . .
Связь тем теснее, чем ближе  к единице ( к единице ( ). Применяется таблица Чеддока для характеристики тесноты связи между случайными величинами ). Применяется таблица Чеддока для характеристики тесноты связи между случайными величинами 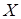 и и  : :
Диапазон измерения
выборочного 
| Характер тесноты
| | 0,1-0,3
0,3-0,5
0,5-0,7
0,7-0,9
0,9-0,99
| слабая
умеренная
заметная
высокая
линейная
|
Если  , то при возрастании одной случайной величины другая имеет тенденцию в среднем возрастать. Если , то при возрастании одной случайной величины другая имеет тенденцию в среднем возрастать. Если  , то при возрастании одной случайной величины другая имеет тенденцию в среднем убывать. , то при возрастании одной случайной величины другая имеет тенденцию в среднем убывать.
Если  , то линейная корреляционная связь отсутствует, и случайные величины называются некоррелированными. Выборочный коэффициент корреляции равен среднему геометрическому выборочных коэффициентов регрессии , то линейная корреляционная связь отсутствует, и случайные величины называются некоррелированными. Выборочный коэффициент корреляции равен среднему геометрическому выборочных коэффициентов регрессии  . Знак коэффициента корреляции совпадает со знаком коэффициентов регрессий. . Знак коэффициента корреляции совпадает со знаком коэффициентов регрессий.
Чтобы сделать обоснованные выводы о тесноте зависимости между случайными величинами 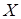 и и  по опытным данным, нужно установить значимость коэффициента корреляции, т. е. проверить нулевую гипотезу по опытным данным, нужно установить значимость коэффициента корреляции, т. е. проверить нулевую гипотезу  о том, что о том, что  . Поиск критических значений осуществляется с помощью t-критерия Стьюдента. . Поиск критических значений осуществляется с помощью t-критерия Стьюдента.
По опытным данным вычисляют критерий проверки
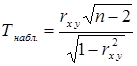 . [3, стр.237] . [3, стр.237]
При заданном уровне значимости  и числу степеней свободы и числу степеней свободы  находят критическое значение находят критическое значение  для двусторонней критической области по таблице Стьюдента. для двусторонней критической области по таблице Стьюдента.
Если  , то выдвинутую гипотезу , то выдвинутую гипотезу  принимают, т. е. выборочный коэффициент незначим, а случайные величины принимают, т. е. выборочный коэффициент незначим, а случайные величины 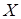 и и  некоррелированные. некоррелированные.
Если  - гипотезу - гипотезу  отвергают, т. е. выборочный коэффициент корреляции значимо отличается от нуля, а случайные величины коррелированны. отвергают, т. е. выборочный коэффициент корреляции значимо отличается от нуля, а случайные величины коррелированны.
Для предыдущего примера определим тесноту связи и вычислим коэффициент корреляции, для чего используем расчетную таблицу.


Таким образом можно сделать вывод что связь между заработной платой и текучестью раб силы очень тесная и обратная, т.е. полученный коэффициент корреляции отрицательный, это говорит о том, что чем меньше заработная плата (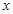 ) тем больше увольнений. ) тем больше увольнений.
Рассчитаем уровень значимости коэффициента корреляции с помощью t-критерия Стьюдента.

По таблице 16 приложения 1 для t-критерия Стьюдента находим критические значения число степеней свободы  ; [3, стр. 492] ; [3, стр. 492]

Строим ось значимости

Величина  попала в зону значимости, поэтому принимается гипотеза попала в зону значимости, поэтому принимается гипотеза  , т.е. коэффициент корреляции значимо отличается от нуля. Можно сделать вывод о том, что чем меньше заработная плата, тем больше увольнений рабочих. , т.е. коэффициент корреляции значимо отличается от нуля. Можно сделать вывод о том, что чем меньше заработная плата, тем больше увольнений рабочих.
Коэффициент детерминации
Число  называется коэффициентом детерминации Y на X. Он показывает, какая часть изменения величины Y может быть объяснена изменением величины X. называется коэффициентом детерминации Y на X. Он показывает, какая часть изменения величины Y может быть объяснена изменением величины X.
Коэффициенты детерминации может принимать значения от 0 до 1. Чем больше этот показатель, тем больше влияние изучаемого фактора на дисперсию зависимой переменной.
Выясним, какая часть вариации у обусловлена корреляцией х. Вычислим коэффициент детерминации  т.е. вариация текучести рабочей силы ( т.е. вариация текучести рабочей силы (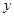 ) на 92% обусловлена вариацией заработной платы ( ) на 92% обусловлена вариацией заработной платы (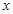 ). ).
 
Тема 3: Линейная многофакторная  регрессионная модель регрессионная модель   
Постановка задачи
Исследовать зависимость одной зависимой переменной (Y) от нескольких объясняющих переменных (Х 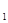 , Х , Х  ,...,Х ,...,Х  ) в условиях конкретного места и конкретного времени. ) в условиях конкретного места и конкретного времени.
Эту задачу можно решить с помощью  множественного или многофакторного регрессионного анализа. множественного или многофакторного регрессионного анализа. 
Уравнение линейной множественной регрессии записывается в виде
 Y = а Y = а 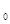 + а + а 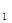 X X 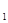 +а +а  X X  +…+ +…+  а а  X X  . .
Объясняющие переменные Х 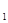 , Х , Х  ,...,Х ,...,Х  оказывают совместное одновременное влияние на зависимую переменную У. Так как всех причин влияющих на результативный показатель (У) охватить нельзя, (ограничившись, только важными объясняющими переменными), то в выражение функции регрессии вводят возмущающую переменную, дающую суммарный эффект от оказывают совместное одновременное влияние на зависимую переменную У. Так как всех причин влияющих на результативный показатель (У) охватить нельзя, (ограничившись, только важными объясняющими переменными), то в выражение функции регрессии вводят возмущающую переменную, дающую суммарный эффект от  воздействия всех неучтенных факторов и случайностей, тогда эмпирические значения У можно представить воздействия всех неучтенных факторов и случайностей, тогда эмпирические значения У можно представить
У= Y +U.
Рассмотрим функцию линейной множественной регрессии с двумя объясняющими переменными
Y= а 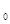 + а + а 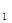 X X 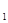 +а +а   X X  . .
Исходные данные запишем в матричном виде
У=   , ,  Х= Х=  . . 
Задача состоит в оценке параметров а 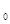 , а , а  ,а ,а  регрессии по результатам выборочных наблюдений над переменными, включенными в анализ. Поставим условие, согласно которому регрессия должна по возможности хорошо согласовываться с эмпирическими данными. Поэтому выдвигаем требование, по которому сумма квадратов отклонений всех наблюдаемых значений зависимой переменной от значений, вычисленных по уравнению регрессии (т.е. сумма квадратов остатков) должна быть минимальной. регрессии по результатам выборочных наблюдений над переменными, включенными в анализ. Поставим условие, согласно которому регрессия должна по возможности хорошо согласовываться с эмпирическими данными. Поэтому выдвигаем требование, по которому сумма квадратов отклонений всех наблюдаемых значений зависимой переменной от значений, вычисленных по уравнению регрессии (т.е. сумма квадратов остатков) должна быть минимальной.
S (а 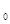 , а , а 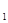 ,а ,а  ) = ) =  = =     min. min.
Находим частные производные по а 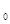 , а , а 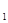 ,а ,а  и приравниваем к нулю. Т. о. будет получена стандартная форма системы нормальных уравнений: и приравниваем к нулю. Т. о. будет получена стандартная форма системы нормальных уравнений:
  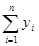  = а = а 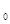 n + a n + a 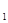  x x 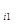 + a + a   x x   

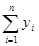 x x  = а = а   x x  + a + a 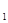  x x   + a + a   x x  x x 
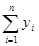 x x  = а = а 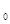  x x  + a + a 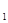  x x  x x  +a +a   x x  
Коэффициенты системы нормальных уравнений перед переменными а 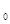 , а , а 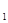 ,а ,а  представляют собой XX представляют собой XX  .Найдем произведение двух матриц Х и Х .Найдем произведение двух матриц Х и Х  
Х = 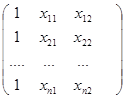 X X  = = 
X  X= X=  . . 
Найдем произведение X  У= У=  . .
Т.о. систему нормальных уравнений можно записать
X  X X  = X = X  У У
Если матрица X  X обратима, то, умножив слева на (X X обратима, то, умножив слева на (X  X) X)  получим получим   = (X = (X  X) X)  (X (X  У). У). 
Вычислив X  X, (X X, (X  X) X)  ,(X ,(X  У), (X У), (X  X) X)  (X (X  У), найдем значения а У), найдем значения а 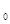 , а , а 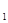 ,а ,а  . .
Выражение X  X можно записать для любого числа объясняющих переменных. X можно записать для любого числа объясняющих переменных.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




