|
|
Power Budget for Two Sources ⇐ ПредыдущаяСтр 2 из 2 Consider first a single source of current, J, immersed in a volume, V, bounded by a surface, S. By inserting Maxwell’s equations into the relationship
One obtains
Хрень Integrating this expression over V leads to the (real) power budget
The surface term is the power radiated to the region exterior to S, and the volume term represents the power, PJ,, furnished by the sources The same kind of analysis can now be applied to a system of two sources, J1 and J2, (which may be considered to form a simple two-element array). When they radiate individually in space, these sources generate respective fields
A similar relationships holds for the “2” fields. When equation is applied to the total field E=E1+E2, H=H1+H2 it yields
The surface integral may be written in more detail as Формула The first two terms are the powers radiated individually by J1, and J2, and the third term is a power interaction term, which must be carefully kept in the analysis. It is clear from the presence of that “combined” term that radiated powers do not add up, except under special conditions. The point is illustrated by the examples discussed in Section 4. On the source side of Equation, we may similarly write. Формула Here again the combined effects за the sources generate an interaction term, which may either increase or decrease the total power provided by the sources with respect to the sun of the individual powers. In the evalution of scattered fields, surface S is often taken to be a spherical surface of very large radius R, on which the fields have their far-field values Формула In these expressions, К is the distance to a common phase-refence point, O, F1 and F2 are functions of 0 and φ, and Ro is the characteristic impedance, of free space. The radiated power, Equation, now becomes Формула Where is on elementary solid angle, and the integration is over all directions. In many applications, J1 is the source of an incident field and J2 represents the correction induced in a scatterer. For such a case, (E2H2) are the scattered fields (ESC,HSC). If the incident fields are those of a plane wave Формула We note it Формула Is the power scattered by the obstacle, assumed to radiate alone in space, while Формула May be called the excitation power. A Few Simple Combined Sources This section illustrates the influence of the interaction term by discussing four very simple problems. The first one concerns the two-dimensional configuration of two z-oriented currents, I1 and I2. The radiated fields from a single current, I, are of the form Формула The power radiated by that source (in W per m along the axis) is Формула In the presence of two equal sources (i.e., with I1=I2=I) the total far fields is Формула Giving a radiated power Формула The factor For anti-parallel currents (i.e., for I1=-I2=I) Формула At small (kol), the two currents form a dipole line, and the two sources together radiate a power Формула That power approaches zero with kol, fundamentally because (+I) and (-I) interfere more and more destructively as their mutual distance decreases. The same kind of behavior holds in three dimensions. For example, consider the two equal electric dipoles shown in Figure 66. The fields stemming from Pel are Формула With respect to the phase center, O. Хрень The power radiated by an individual dipole is easily found to be Формула For the two dipoles together, Формула The leading factor is the sum of the individual radiated powers. The double integral term represents the interaction. For small (kol), Prad becomes Формула Assume, as a final exercise, that Pel in Figure 6b is left untouched, but that Pe2 is replaced by a similarly located and oriented magnetic dipole Pm. The radiation fields of Pm are Формула   Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем... 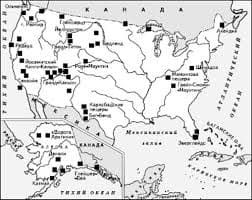 Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам...  ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между... 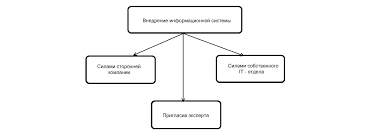 Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|