|
|
Потенциальная и кинетическая энергии ⇐ ПредыдущаяСтр 6 из 6 Установим изменение потенциальной и кинетической энергий колеблющейся системы. Известно, что потенциальная энергия упруго деформированного тела равна
Кинетическая энергия
Анализ (7) и (8) показывает, что когда одна из энергий E=Wn+Wk=kA2/2 (9) остается величиной постоянной и для пружинного маятника, (см. рис. 1), она определяется работой, совершенной внешней силой по сжатию или растяжению пружины. Итак, мы рассмотрели свободные или собственные колебания, которые происходят в системе, предоставленной самой себе, после того, как она была выведена из положения равновесия. Но в реальных условиях всегда на механические системы действуют силы трения из-за чего свободные колебания переходят в затухающие, которые будут рассмотрены в параграфе 8. Векторная диаграмма гармонического колебания Гармоническое колебание
можно представить в виде проекции вектора Комплексная форма представления колебаний
Поэтому уравнение гармонического колебания (3) можно записать в экспоненциальной форме:
 .
Вещественная часть Обычно обозначение
5. Сложение одинаково направленных колебаний Рассмотрим сложение двух гармонических колебаний одинаковой частоты, смещения которых Используем векторную диаграмму, рис. 4; откуда следует, что
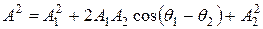
Пусть
6.1. Пусть 6.2. При (x2/A2)+(y2/B2)=1. При разных частотах складывающихся колебаний результирующие траектории будут иметь более сложный вид. Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Гармонические осцилляторы Математический маятник
Хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити, рис. 7. Тангенциальное ускорение а, возникает под действием тангенциальной силы
 соотношением:  .
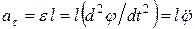Из второго закона Ньютона следует, что Деля правую и левую части этого уравнения на l, получим:
где
где
Таким образом, период колебаний математического маятника T0, не зависит от его массы и амплитуды колебаний. Измерения T0 дают возможность с большой точностью определять g, что позволяет проводить гравитометрическую разведку и определять форму фигуры планеты. Математический маятник сыграл большую роль в открытии закона сохранения энергии и в создании общей теории относительности, основным положением которой является равенство массы гравитационной и инертной. Пружинный маятник Это груз массой т, подвешенный на абсолютно упругой пружине и совершающий колебания около положения равновесия, рис. 1. Он был рассмотрен в параграфе 1. Для него
 , который сообщает угловое ускорение  , где J - момент инерции тела, относительно оси, проходящей через точку О перпендикулярно рисунку.
С учетом этого получается дифференциальное уравнение где Решением его будет Период колебания где L = J/ml - приведенная длина физического маятника; L - это длина такого математического маятника, период колебаний которого совпадает с периодом колебания данного физического маятника. Точка О', расположенная на расстоянии L от точки О (рис. 8), через которую проходит ось подвеса физического маятника, называется его центром качаний. Периоды колебаний относительно точек О и О' совпадают.   ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала...  ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между...  Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам...  Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? - задался я вопросом... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|
, где k - коэффициент упругости, х - смещение; откуда для потенциальной энергии колебаний находим
. (7)
, что, согласно (2) и (5), в нашем случае будет
. (8)
или 
увеличивается, то другая уменьшается. Полная же энергия
, вращающегося против хода часовой стрелки с угловой скоростью, равной круговой частоте 
. Из рис. 3 следует, что проекция вектора 
на направление ОХ будет 
Согласно формуле Эйлера для комплексных чисел
, где 
.
представляет собой смещение х при гармоническом колебании 
.
опускают и пишут так
.
и 
.
где
.
, тогда
, т.е. результирующее колебание не будет гармоническим. Если колебания мало отличаются по частоте, например, 
, 
, то результирующее колебание 
можно рассматривать как почти гармоническое колебание с частотой 
и медленно меняющейся амплитудой 
. Такие периодические изменения амплитуды называются биениями.
и 
, тогда траекторией будет прямая линия, рис. 5: 
.
, траекторией будет эллипс, (рис. 6):
Это материальная точка, подвешенная на невесомой, нерастяжимой нити.
. Для малых 
можно положить 
и 
.
, или 
.
, (10)
. Решением его для малых φ будет:
, (11)
. (12)
и 
(13)
7.3. Физический маятник
. Разделив правую и левую части последнего уравнения на момент инерции тела J, найдем: 
,
. (14)
.
, (15)