|
|
Общефизический закон сохранения энергииКлассическая механика учитывает только кинетическую энергию макроскопического движения тел и их макроскопических частей, а также их потенциальную энергию. Но она полностью отвлекается от внутреннего атомистического строения вещества. При ударе, трении и аналогичных процессах кинетическая энергия видимого движения тел не пропадает. Она только переходит в кинетическую энергию невидимого беспорядочного движения атомов и молекул вещества, а также в потенциальную энергию их взаимодействия. Эта часть энергии получила название внутренней энергии. Беспорядочное движение атомов и молекул воспринимается нашими органами чувств в виде тепла. Таково физическое объяснение кажущейся потери механической энергии при ударе, трении и пр. В физике закон сохранения энергии распространяют не только на явления, рассматриваемые в механике, но на все без исключения процессы, происходящие в природе. Полное количество энергии в изолированной системе тел и полей всегда остается постоянным; энергия лишь может переходить из одной формы в другую. В основе закона сохранения энергии лежит такое свойство времени как однородность, т.е. равнозначность всех моментов времени, заключающаяся в том, что замена момента времени t 1 моментом времени t 2, без изменения значений координат и скоростей тел не изменяет механических свойств системы. Поведение системы, начиная с момента времени t 2 будет таким же, каким оно было бы, начиная с момента t 1. Общефизический закон сохранения энергии не может быть выведен из уравнений механики, и должен рассматриваться как одно из наиболее широких обобщений опытных фактов. ЛЕКЦИЯ №6. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА Момент силы и момент импульса относительно неподвижного начала Пусть О – какая-либо неподвижная точка в инерциальной системе отсчета. Ее называют началом или полюсом. Обозначим через Моментом силы
Моментом
Отметим частный случай двух равных параллельных сил Такие силы образуют так называемую пару сил. В этом случае
т. е. момент пары сил равен моменту одной из этих сил относительно точки приложения другой. Очевидно, что момент пары сил не зависит от выбора точки О. В частности, если равные и противоположно направленные силы Моментом импульса материальной точки относительно точки О называется векторное произведение радиуса-вектора
Для системы n материальных точек моментом импульса относительно некоторой точки О называется векторная сумма моментов импульсов этих точек относительно того же начала:
Уравнение моментов Предположим, что точка О неподвижна. В случае одной материальной точки, дифференцируя (3), получаем
При неподвижной точке О вектор Таким образом
 Это уравнение моментов для одной материальной точки. Распространим его на систему материальных точек, для чего запишем уравнение (5) для каждой материальной точки механической системы, понимая под М момент всех действующих на нее сил, как внутренних так и внешних. Затем сложим все эти уравнения. Внутренние силы входят в систему попарно так, что Это уравнение моментов для одной материальной точки. Распространим его на систему материальных точек, для чего запишем уравнение (5) для каждой материальной точки механической системы, понимая под М момент всех действующих на нее сил, как внутренних так и внешних. Затем сложим все эти уравнения. Внутренние силы входят в систему попарно так, что  где где  – сила воздействия k -й материальной точки на i -ю. Кроме того, эти силы – сила воздействия k -й материальной точки на i -ю. Кроме того, эти силы  и и 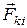 , действуют вдоль одной и той же прямой. Момент таких двух сил, а значит и моменты всех внутренних сил равны нулю. В результате опять получается уравнение моментов типа (5) только для системы материальных точек, в котором , действуют вдоль одной и той же прямой. Момент таких двух сил, а значит и моменты всех внутренних сил равны нулю. В результате опять получается уравнение моментов типа (5) только для системы материальных точек, в котором 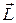 определяется выражением (4), а определяется выражением (4), а  – выражением (2) для внешних сил, т. е. – выражением (2) для внешних сил, т. е.
Моментом силы механической системы относительно оси называется проекция на эту ось вектора момента силы системы относительно любой точки, выбранной на рассматриваемой оси (рис. 2). Соответственно, моментом импульса относительно оси называется проекция на эту ось вектора момента импульса относительно любой точки на данной оси. Можно доказать, что выбор точки на оси влияет на значения моментов импульса Если мы выбираем прямоугольную систему координат с началом, совпадающим с полюсом, то имеем:
  Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор...  Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все...  ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала...  Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|