|
|
N-мерное векторное пространство. Операции над векторами. ⇐ ПредыдущаяСтр 4 из 4 Произвол-й упоряд-й набор из n действ-ых чисел наз-я n-мерным вектором, сами числа наз-я координаты вектора X={x1,…xn}. Вектор. - Упорядочен сов-ть (x1, x2,..., x n) n веществ-х чисел наз n-мерным век-м, а числа xi (i =) - компонентами, или координатами, вектора. Пример. Если, например, нек-й автом-й завод должен выпустить в смену 50 легк автом-й, 100 груз, 10 автобусов, 50 комп-в запчастей для легк авт-й и 150 комп для груз авт-й и автоб-в, то произв-ю программу этого завода можзапи в виде вект (50, 100, 10, 50, 150), имеющ пять компонент. Суммой/разностью 2х векторов наз-я 3й вектор A+/-B={A1+/-B1,…An+/-Bn}. Альфа*A ={альфа*A1,…альфа*An} – вектор * на число A*B=(A,B)=A1*B1+…+An*Bn – вектор на вектор Сов-ть всех n-мерных векторов после ведения операций сложения и вычитания наз-ся n-мерное векторное пространство C1X1+…CnXn=C*X
| 21. Целочисленнон и частично целочисл программ-е
Целочисленное программирование — разновидность линейного программирования, подразумевающая, что искомые значения должны быть целыми числами.
Простейший метод решения задачи целочисленного программирования — сведение ее к задаче линейного программирования с проверкой результата на целочисленность.
Метод Гамори:
1. На первом этапе за-ча рещ-я без условия цело-ти;
2. стро-ся система доп ограни-й
В прцессе работы по этому методу либо выясн-ся целочисл ре-ние,либо то что его нет.
Недостатки метода:
Требование целочисл-ти для всех переем-х, вкл допол-е.
При решении задач целочисл просматриваются коэф-ы в строке В. Если хотя бы в одной из таких строк осутствуют дробные коэф в столбцах А, то за-ча целочис прогр не имеет реше-я. Для дробных коэф-в столбца Врассчит дробные части. Построение доп огран осущ-л по той строке в кот стои макси qi
Доп огр:
qi1x1+qi2x2+…+qinxn-qi>=0, где qij-это дробные части коэф i-ой строки.
При частично целочисл прогр процедура решения аналогична методу Гамори,с той лишь разницей, что доп огранм-ие строится по другому:
Li1x1+ Li2x2+…+ Linxn-qi>=0, если хк-нецелое, то Liк=хiк,если xiк>=0;
qi/(1-qi)*|xik|, если хiк<0.
Хк-целое
Lik=qik, если qik<=qi;
qi/(1-qi)* (1-qik), если qik>qi.
10. Задачи лин прогр-ия: опр-я, постан-ка, прим.
Лин прогр-ие - это наука о методах исследования и отыскания наиб и наим знач-ий лин ф-ии, на неизвестн кот наложены лин ограничения. Т.обр, задачи лин прогр относ к задачам на усл-й экстр-ум ф-ии.
Даны лин-я функция f = С1х1+С2х2+... +СnXn (1)
и система линейных ограничений
a11x1 + a22x2 +... + a1nХn = b1
a21x1 + a22x2 +... + a2nХn = b2
ai1x1 + ai2x2 +... + ainХn = bi
aM1x1 + aM2x2 +... +amn Xn = bm (2)
(j = 1, 2,...,n) где аij, Ьj и Сj - заданные постоянные величины.
Найти такие неотриц знач-ия х1, х2,..., хn, кот удовлетворяют системе ограничений (2) и доставляют линейной функции (1) миним знач-е.
Общая задача имеет несколько форм записи.
Векторная форма записи. Минимизировать лин ф-ию f = СХ при ограничениях (1.4) А1х1 + А2x2 +... + Аnxn = B, (4) x≥0.
где С = (с1, с2,..., сn); Х = (х1, х2,..., хn); СХ - скалярное произведение; векторы
A1, A2,..., An, B состоят соответственно из коэф-ов при неизвестных и свободных членах.
Матричная форма записи. Минимизировать лин ф-ию, f = СХ при ограничениях
АХ = B, x≥0, где С = (с1, с2,..., сn) - матрица-cтрока; А = (аij) - матрица системы;
Х - матрица-столбец, B - матрица-столбец
Запись с помощью знаков суммирования. Минимизировать линейную функцию
f = Сjхj при ограничениях.
0пр 1. Планом или допустимым решением задачи линейного программирования называется Х = (х1, х2,..., хn), удовлетворяющий условиям (2) и (3).
0пр 2. План Х = (х1, х2,..., хn) наз опорным, если векторы А (i = 1, 2,..., n), входящие в разложение (4) с положит коэффициентами х, явл линейно независимыми.
Т.к. векторы А являются т-мерными, то из определения опорного плана следует, что число его полож-х компонент не может превышать m.
0пр 3. Опорный план наз невырожденным, если он содержит m полож-х компонент, в противном случае опорный план называется вырожденным.
0пр 4. Оптимальным планом или оптимальным решением задачи лин программирования наз план, доставляющий наим (наиб) значение лин ф-ии.
11. Графический мет реш-я задач лин прогр-ия.
Графич метод основан на геометрич интерп-ции задачи лин прогр и прим-ся в основном при решении задач двумерного пространства и только некоторых задач трехмерного пространства, т.к. довольно трудно построить многогранник решений, кот образуется в результате пересеч-я полупрост-тв. Задачу простр-ва размерности больше трех изобразить граф-ки вообще невозм.
Графич метод состоит из 2-х этапов. На 1-ом этапе необходимо построить многогранник решений. На 2-ом этапе необх найти min-ое знач-ие целевой ф-ии. Осуществление 2-го этапа возм-но 2-мя способами: 1) вычислить коор-ты всех угловых точек, подставить их в целевую ф-ия и та из них, кот будет доставлять min-ое знач-ие цел ф-ии будет явл-ся решением. 2) Используя св-ва градиента цел ф-ии срвзу опр-ть min-ое знач-ие целевой ф-ии.
Пусть задача линейного программирования задана в двумерном пространстве, т. е. огран-я содерж две переменные.
Найти минимальное значение функции
f = С1х1+С2х2 (1) при
a11x1 + a22x2 b1
a21x1 + a22x2 b2
........
am1x1 + am2x2 bm (2)
х1≥ 0, х2≥ 0 (3)
Допустим, что сист (2) при усл (3) совме-на и ее многоугольник решений ограничен. Каждое из неравенств (2) и (3), определяет полуплоскость с граничными прямыми: ai1x1 + ai2x2 + ai3x3 =bi,(i = 1, 2,..., n), х1=0, х2=0. Линейная функция (1) при фиксированных знач-х f является уравнением прямой линии: С1х1 + С2х2 = const.
Построим многоугольник решений системы ограничений (2) и график линейной функции (1) при f = 0/ Тогда поставленной задаче лин
програм можно дать следующую интерпретацию. Найти точку
многоугольника решений, в кот прямая С1х1 + С2х2 =const опорная и ф-ция f при этом дост-т мин-а.
Значения f = С1х1 + С2х2 возр-т в направлении вектора N =(С1, С2), поэтому прямую f = 0 передвигаем параллельно самой себе в направлении вектора Х. Координаты т. экстремума А (х1, х2) находим, решая сист уравнений прямых, пересекающихся в этточке.
23. Транспортная задача закрыт типа.
Треб составления плана однород груза, чтоб общая ст-ть перевозок была миним. Есть m – пунктов отправления (поставщики), n - пунктов назначения (потребители), ai- кол-во груза в i пункте отправления (i=1,m), bj – треб кол-во груза в j пункте назначения (j=1,n), cij – ст-ть перевозки груза из i пункта отправления в j пункт назначения, xij – кол-во груза которого необх перевезти из i пункта отправления в j.
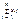 - кол-во груза, вывезенное от i поставщика ко всем потребителям; - кол-во груза, вывезенное от i поставщика ко всем потребителям;  - кол-во груза, ввезенное j потребителю от всех поставщиков; cij – ст-ть перевозок от i поставщика к j потребителю; - кол-во груза, ввезенное j потребителю от всех поставщиков; cij – ст-ть перевозок от i поставщика к j потребителю;  - ст-ть перевозок груза всем потребителям от i поставщика. - ст-ть перевозок груза всем потребителям от i поставщика.  - суммарная ст-ть перевозок. - суммарная ст-ть перевозок.
 →min, →min,  ≤aij, i=1,m, ≤aij, i=1,m, 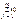 ≤bij, j=1,n, xij≥0
Когда суммарное потребление=суммарным запасам, то это задача закрытого типа ≤bij, j=1,n, xij≥0
Когда суммарное потребление=суммарным запасам, то это задача закрытого типа
 , , 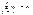 , i=1,m; , i=1,m; 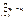 , j=1,n
Теорема 1: любая трансп задача закрытого типа имеет решение.
Метод потенциалов. Теорема 2: если х*= {xij*}, то оптимал решение соотв системе из (m+n) чисел, ui* и vj* таких что ui+vj=cij, xij>0, ui+vj<=cij, xij=0. ui, vj – это потенциалы поставщиков и потребителей. Для решения задач нужен базис, т е первое опорное решение.
Методы построения первонач плана перевозок.
Метод сев-зап угла.
Метод миним ст-ти. Просматривается вся матрица перевозок, и из нее выбирается позиция с наименьшим значением, затем просматриваются значения наличия запасов на складе A и потребности у потребителя B, затем в данную клетку записывается величина D=MIN(A,B). Из запасов соответствующего склада и потребностей магазина вычитается величина D. Если запас товара на складе исчерпан, то эта строка исключается из дальнейшего рассмотрения. Если потребность магазина в товаре удовлетворена полностью, то этот столбец исключается из дальнейшего рассмотрения. Может быть случай, когда одновременно исключаются и строка и столбец, этот случай называется вырожденным. В дальнейшем весь процесс повторяется до тех пор, пока не будет исчерпан весь запас товаров на складах и не будет удовлетворена потребность всех магазинов. По полученной матрице перевозок вычисляется целевая функция задачи.
Метод двойного предпочтения. Э тот метод похож на метод минимальной ст-ти, но для столбцов. Просматривается первый столбец матрицы, в нем находится наименьший элемент. Затем проверяется, минимален ли этот элемент в своей строке. Если элемент минимален в своей строке, то по методу минимального элемента в эту клетку заносится значение D=MIN(A,B),соотв запас и потребность ум на эту величину. Обнулившаяся строка или столбец исключаются из рассм и процесс повторяется, начиная с первого неисключенного столбца. Если найденный миним элемент не минимален в своей строке, то происходит переход к следующему столбцу и так до тех пор, пока не будет найден такой элемент. По полученной матрице перевозок вычисляется целевая функция.
Пример.
4 поставщика и 5 потребителей, известны запасы поставщиков и потребности потребителей, также ст-ть перевозок 1 ед п-ции от поставщика до потребителя.
Метод двойного предпочтения. , j=1,n
Теорема 1: любая трансп задача закрытого типа имеет решение.
Метод потенциалов. Теорема 2: если х*= {xij*}, то оптимал решение соотв системе из (m+n) чисел, ui* и vj* таких что ui+vj=cij, xij>0, ui+vj<=cij, xij=0. ui, vj – это потенциалы поставщиков и потребителей. Для решения задач нужен базис, т е первое опорное решение.
Методы построения первонач плана перевозок.
Метод сев-зап угла.
Метод миним ст-ти. Просматривается вся матрица перевозок, и из нее выбирается позиция с наименьшим значением, затем просматриваются значения наличия запасов на складе A и потребности у потребителя B, затем в данную клетку записывается величина D=MIN(A,B). Из запасов соответствующего склада и потребностей магазина вычитается величина D. Если запас товара на складе исчерпан, то эта строка исключается из дальнейшего рассмотрения. Если потребность магазина в товаре удовлетворена полностью, то этот столбец исключается из дальнейшего рассмотрения. Может быть случай, когда одновременно исключаются и строка и столбец, этот случай называется вырожденным. В дальнейшем весь процесс повторяется до тех пор, пока не будет исчерпан весь запас товаров на складах и не будет удовлетворена потребность всех магазинов. По полученной матрице перевозок вычисляется целевая функция задачи.
Метод двойного предпочтения. Э тот метод похож на метод минимальной ст-ти, но для столбцов. Просматривается первый столбец матрицы, в нем находится наименьший элемент. Затем проверяется, минимален ли этот элемент в своей строке. Если элемент минимален в своей строке, то по методу минимального элемента в эту клетку заносится значение D=MIN(A,B),соотв запас и потребность ум на эту величину. Обнулившаяся строка или столбец исключаются из рассм и процесс повторяется, начиная с первого неисключенного столбца. Если найденный миним элемент не минимален в своей строке, то происходит переход к следующему столбцу и так до тех пор, пока не будет найден такой элемент. По полученной матрице перевозок вычисляется целевая функция.
Пример.
4 поставщика и 5 потребителей, известны запасы поставщиков и потребности потребителей, также ст-ть перевозок 1 ед п-ции от поставщика до потребителя.
Метод двойного предпочтения.
Процедура работы по методу потенциалов Х11+х12+х13+х14+х15=100 Х21+х22+х23+х24+х25=250 Х31+х32+х33+х34+х35=200 Х41+х42+х43+х34+х45=300 Х11+х21+х31+х41=200 .................... Х51+х52+х53+х54=250 Этап 1. Основан на теореме 2, т к д\ занятых клеток ui+vj=cij будем записывать систему ур-ий из потенциалов u1+v4=1; u2+v1=2; u2+v3=7; u3+v5=2; u4+v5=8; u4+v3=12; u4+v5=13; u3+v4=2. В любом опорном плане перевозок заполн клеток должно быть (m+n-1). Т к клеток 7, то введем одну фиктивно заполненную клетку. Приравниваем к 0 тот потенциал, к-ый сотв наиб заполненной строке или столбцу u4=0; v2=8; v5=13; v3= 12; u2= -1; u3=-11; v4=13; u1=-12; v1=3.
Этап 2. Проверка условия оптимал для не занятых клеток ui+vj=cij Сумма потенциалов д\ не занят клеток (числа со штрихом)наз косвенными стоимостями. Этап 3. Выбор клетки в к-ую следует перевести груз, это клетка явл той где мах расхождение. Этап 4. Построение цикла и определение величины перевозимого груза.
Велич перев-го груза это есть min из всех ячеек отмеч-х со зн-м «-».
Эт 5. Осущ перераспределение груза
  Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор...  Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...  ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала...  Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? - задался я вопросом... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|