|
ПРИМЕР ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СИСТЕМЫ И ЕЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
Рассмотрим схему, изображенную на рис. 3, состоящую из трех контуров, связанных емкостью С3. Требуется найти передаточную функцию. Необходимо отметить, что механические и электрические системы могут описываться одинаковыми по форме дифференциальными уравнениями.
В соответствии с изложенной в пункте 1.1 методикой построения математической модели системы необходимо написать систему уравнений с использованием законов Кирхгофа:
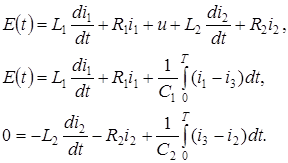
Учитывая данные, приведенные в Приложении А, преобразуем эти уравнения по Лапласу при нулевых начальных условиях
 (16) (16)
Решая эту систему уравнений относительно  из второго и третьего уравнений находим из второго и третьего уравнений находим
 (17) (17)
Подставив эти значения в (16) получим
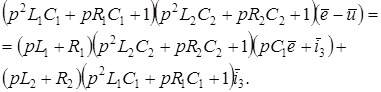
Выразим  через напряжение u на конденсаторе через напряжение u на конденсаторе
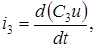
тогда  . Подставляя это значение в (17) получим . Подставляя это значение в (17) получим
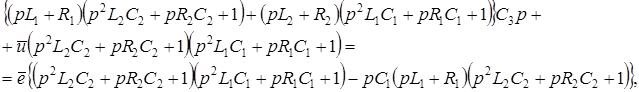 откуда в силу (10) откуда в силу (10)
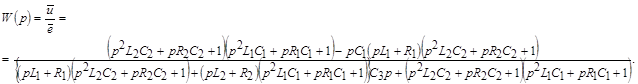
ВСТРОЕННЫЕ ФУНКЦИИ MATHCAD
Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.
Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределённых вычислений и традиционных языков программирования. Также этот пакет прикладных программ часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам. Перечень основных функций, используемых в Mathcad, приведен в таблице 1.2.
Таблица 1.2 - Перечень основных встроенных функций MATHCAD
| Функция
| Аргументы
| Описание
| | angle (x,y)
| x, у - координаты точки
| Угол между точкой и осью х
| | APPENDPRN(file)
| File - строковое представление пути к файлу
| Дозапись данных в существующий текстовый файл
| | arg (z)
| z - аргумент функции
| Аргумент комплексного числа
| | atan2 (x,y)
| х, у - координаты точки
| Угол, отсчитываемый от оси х до точки (х,у)
| | augment (A, B, C,)
| А, В, С,...-векторы или матрицы
| Слияние матриц слева направо
| | Bulstoer (yO,tO,tl,M,D)
| См. rkfixed
| Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера
| | bulstoer(yO,tO,tl, ace, D, k, s)
| См. rkadapt
| Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера (для определения только последней точки
интервала)
| | ceil (x)
| х - аргумент
| Наименьшее целое, не меньшее х
| | cfft(y), CFFT(y)
| у - вектор данных
| Вектор прямого комплексного преобразования Фурье (в разных нормировках)
| | cols (A)
| A - матрица или вектор
| Число столбцов
| | cos (z)
| z - аргумент
| Косинус
| | cosh(z)
| z - аргумент
| Гиперболический косинус
| | cot(z)
| z - аргумент
| Котангенс
| | coth (z)
| z - аргумент
| Гиперболический котангенс
| | csort (A, i)
| А - матрица i -индекс столбца
| Сортировка строк матрицы по элементам i -го столбца
| | csc(z)
| z - аргумент
| Косеканс
| | csch(z)
| z - аргумент
| Гиперболический косеканс
| | csgn(z)
| z - аргумент
| Комплексный знак числа
| | cspline (x,y)
| x, у - векторы данных
| Вектор коэффициентов
кубического
сплайна
| | diag(v)
| v - вектор
| Диагональная матрица, на диагонали которой находятся элементы вектора
| | erf (x)
| х - аргумент
| Функция ошибок
| | erfc(x)
| х - аргумент
| Обратная функция ошибок
| | exp(z)
| z - аргумент
| Экспонента в степени z
| | fft (y), FFT(y)
| у - вектор данных
| Вектор прямого преобразования Фурье (в разных нормировках)
| | Find (x1,x2,...)
| x1, х2,... -переменные
| Возвращает корень алгебраического уравнения (скаляр) или системы (вектор), определенных в блоке с Given
| | floor (x)
| х - аргумент
| Наибольшее целое число, меньшее или равное х
| | geninv (A)
| А - матрица
| Создание обратной матрицы
| | Given
|
| Ключевое слово для ввода систем уравнений, неравенств и т. п.
| | heaviside step(x)
| х - аргумент
| Функция Хевисайда
| | identity(N)
| N - размер матрицы
| Создание единичной матрицы
| | icf ft (v), ICFFT (v)
| v - вектор частотных данных Фурье-спектра
| Вектор комплексного обратного преобразования Фурье (в разных нормировках)
| | if (cond, x, y)
| cond- логическое условие, х, у -значения, возвращаемые, если условие верно (ложно)
| Функция условия
| | if ft (v), IFFT(v)
| v - вектор частотных данных Фурье-спектра
| Вектор обратного
преобразования
Фурье (в разных нормировках)
| | iwave (v)
| v - вектор частотных данных вейвлет-спектра
| Вектор обратного вейвлет -преобразования
| | Im(z)
| z - аргумент
| Мнимая часть комплексного числа
| | interp(s,x,y,t)
| s - вектор вторых производных; х, у -векторы данных; t - аргумент
| Сплайн-интерполяция
| | Kronecker delta (x, у)
| x,y - аргументы
| Дельта-символ Кронекера
| | last (v)
| v - вектор
| Индекс последнего элемента вектора
| | length (v)
| v - вектор
| Число элементов вектора
| | line (x, y)
| х, у - векторы данных
| Вектор из коэффициентов линейной регрессии b+а-х
| | ln(z)
| z - аргумент
| Натуральный логарифм
| | log(z)
| z - аргумент
| Десятичный логарифм
| | log(z, b)
| z - аргумент
| Логарифм z по основанию b
| | Isolve (A, b)
| А - матрица СЛАУ,
b - вектор правых частей
| Решение системы линейных уравнений
(СЛАУ)
| | Minerr (x1,x2,...)
| x1,x2,... -
переменные
| Возвращает вектор
приближенного решения системы уравнений и
неравенств, определенных в блоке с Given
| | Odesolve (t,t1,[step])
| t- переменная
интегрирования
ОДУ;
t1 - конечная точка
интервала
интегрирования; step - число шагов
интегрирования ОДУ
| Возвращает матрицу с
решением задачи Коши для
одного ОДУ, определенного в
блоке с Given и начальными
условиями в точке t0
| | predict (y, m, n)
| у - исходный
вектор; m - число
элементов у, по
которым строится
экстраполяция; n - количество
предсказываемых элементов
| Функция предсказания,
экстраполирующая вектор
| | rank (A)
| А - матрица
| Ранг матрицы
| | Re(z)
| z - аргумент
| Действительная часть комплексного числа
| | reverse (v)
| v - вектор
| Перестановка элементов вектора в обратном порядке
| | Rkadapt (y0,t0,t1,
acc,D,k,s)
| Y0 - вектор
начальных условий;
(t0,t1) - интервал
интегрирования;
асе - погрешность
вычисления;
D(t,y) - векторная
функция, задающая
систему ОДУ;
k - максимальное
число шагов
интегрирования;
s - минимальный
шаг интегрирования
| Возвращает матрицу с
решением задачи Коши для
системы ОДУ методом Рунге-
Кутты с переменным шагом и
заданной точностью (для
определения только последней
точки интервала)
| | Rkadapt(y0,t0,t1,M,D)
| См. rkfixed
| Возвращает матрицу с решением задачи Коши для системы ОДУ методом Рунге-Кутты с переменным шагом
| | rkfixed(y0,t0,t1,M,D)
| У0 - вектор начальных условий (t0,t1) -интервал интегрирования; M - число шагов интегрирования D(t,y) -векторная функция, задающая систему ОДУ
| Возвращает матрицу с решением задачи Коши для системы ОДУ методом Рунге-Кутты с фиксированным шагом
| | root(f (x,...),x[a,b])
| f (х,...) -функция х - переменная (а,Ь) -интервал поиска корня
| Возвращает корень функции
| | round (x, n)
| х - аргумент;
n - число знаков округления после десятичной точки
| Округление
| | rows (A)
| А - матрица или вектор
| Число строк
| | rref (A)
| А - матрица или вектор
| Преобразование матрицы в ступенчатый вид
| | rsort (A, i)
| A - матрица;
i- индекс строки
| Сортировка матрицы по элементам i-й строки
| | sec(z)
| z - аргумент
| Секанс
| | sech(z)
| z - аргумент
| Гиперболический секанс
| | sign(x)
| х - аргумент
| Знак числа
| | signum(z)
| z - аргумент
| Возвращает 0, если z=0 и z/|z| в остальных случаях
| | sin(z)
| z - аргумент
| Синус
| | sinh(z)
| z - аргумент
| Гиперболический синус
| | sort (v)
| v - вектор
| Сортировка элементов вектора
| | supsmooth(x,y)
| x, у - векторы данных
| Сглаживание с помощью адаптивного алгоритма
| | tan(z)
| z - аргумент
| Тангенс
| | tanh (z)
| z - аргумент
| Гиперболический тангенс
|
ЗАДАНИЯ НА КУРСОВУЮ РАБОТУ
Контрольную работу рекомендуется полностью выполнять с помощью пакета прикладных программ MathCad. Она состоит из следующих этапов:
1. Согласно вашему варианту составить дифференциальные уравнения состояния электрической цепи по второму закону Кирхгофа. Номер схемы выбирается из табл. 2.1. При этом R=500·N·RT; w=1000*(1+k)m0.5; L=LT·R/ w; C=CT/(R·w), где N – последние две цифры номера группы, m - номер варианта, k - последняя цифра текущего года, индекс (T) обозначает табличное значение;
2. Определить зависимости контурных токов от времени, решив систему дифференциальных уравнений;
3. Осуществить переход от временного аргумента к комплексным переменным (преобразование Лапласа);
4. Определить передаточную функцию относительно напряжения u вых на выходе элемента, указанного в табл. 2.1, столбец 8;
5. Определить вид переходного процесса по корням характеристического уравнения;
6. При помощи передаточной функции определить сигнал на выходе системы при подаче сигнала E (t) на вход (таблица 1, второй столбец);
7. Определить амплитудно-частотную и фазочастотную характеристики.
Таблица 2.1
| № вар.
| E (t)
| Инд-ть L, Гн
| Ем-сть C, мФ
| Сопротивление
| № рис. схемы
| Uвых
на эл-те
| | R 1, Ом
| R 2, Ом
| | 1.
| 24Cos(26t)
|
| 0,3
|
| -
|
| R1
| | 2.
| 36Sin(20t)
|
|
|
| -
|
| R1
| | 3.
| 30Cos(163t)
| 0,005
| 7,5
| 0,8
| -
|
| R1
| | 4.
| 36Sin(74t)
| 0,23
| 0,78
| 17,2
| -
|
| R1
| | 5.
| 120Cos(3t)
| 0,678
| 136,3
| 2,23
| -
|
| R1
| | 6.
| 36Sin(50t)
| 2,45
| 0,56
| 66,1
|
|
| R1
| | 7.
| 12Cos(308t)
| 0,0876
| 0,12
|
| -
|
| R1
| | 8.
| 37Sin(151t)
| 0,0163
| 2,67
| 2,5
|
|
| R1
| | 9.
| 220Cos(29t)
| 1,22
| 0,98
|
| -
|
| R1
| | 10.
| 36Sin(21t)
|
| 0,78
|
|
|
| R2
| | 11.
| 124Cos(58t)
| 0,67
| -
|
|
|
| R1
| | 12.
| 36Sin(50t)
| 9,6
| 0,08
|
| -
|
| R1
| | 13.
| 120Cos(58t)
| 0,976
| 0,3
|
| -
|
| R1
| | 14.
| 36Sin(22t)
|
|
|
| -
|
| R1
| | 15.
| 124Cos(18t)
|
| -
|
|
|
| R1
| | 16.
| 36Sin(21t)
|
| 0,78
|
|
|
| R1
| | 17.
| 124Cos(58t)
| 0,67
| -
|
|
|
| R2
| | 18.
| 36Sin(27t)
| 0,97
| 1,45
| 25,8
| -
|
| R1
| | 19.
| 54Cos(15t)
| 0,0163
| 2,67
| 2,5
|
|
| R2
| | 20.
| 136Sin(11t)
| 5,65
| 1,45
| 62,4
| -
|
| R1
| | 21.
| 124Cos(37t)
| 3,93
| 0,19
|
| -
|
| R1
| | 22.
| 136Sin(12t)
| 5,61
| 1,23
|
| -
|
| R1
| | 23.
| 24Cos(12t)
| 1,67
| 4,23
|
| -
|
| R1
| | 24.
| 220Sin(2t)
| 20,85
| 14,23
|
| -
|
| R1
| | 25.
| 124Cos(9t)
| 2,85
| 4,23
|
| -
|
| Ri
| | 26.
| 12Sin(24t)
| 56,34
| 0,03
|
| -
|
| Ri
| | 27.
| 24Cos(38t)
| 3,01
| 0,23
|
| -
|
| Ri
| | 28.
| 12Sin(285t)
| 0,01
| 1,23
|
|
|
| Ri
| | 29.
| 50Cos(30t)
| 0,051
| -
| 1,5
|
|
| Ri
| | 30.
| 220Sin(64t)
| 0,151
| 1,59
|
|
|
| Ri
| | 31.
| 20Cos(6t)
| 0,763
| 35,16
|
| 2,5
|
| Ri
| | 32.
| 99Sin(1,5t)
| 0,931
|
| 1,4
| -
|
| Ri
| | 33.
| 12Cos(0,3t)
| 10,43
| -
|
|
|
| R2
| | 34.
| 36Sin(6t)
| 0,023
|
| 0,1
| -
|
| Ri
| | 35.
| 12Sin(285t)
| 0,01
| 1,23
|
|
|
| R2
| | 36.
| 16Sin(4t)
| 98,5
| 0,56
|
| -
|
| Ri
| |
| 24Cos(1,5t)
| 78,4
| 5,61
|
| -
|
| Ri
| |
| 58Sin(110t)
| 1,45
| 0,056
| 160,8
| -
|
| Ri
| |
| 24Cos(50t)
| 5,94
| -
|
|
|
| Ri
| |
| 36Sin(50t)
|
| 92,1
|
| -
|
| Ri
| |
| 24Cos(50t)
| 5,94
| -
|
|
|
| R2
| |
| 36Sin(1,5t)
|
| 7,56
|
|
|
| R2
| |
| 124Cos(36t)
| 0,12
| 6,46
|
|
|
| Ri
| |
| 220Sin(19t)
| 9,34
| 0,294
|
| -
|
| Ri
| |
| 14Cos(172t)
| 0,29
| 0,117
|
| -
|
| Ri
| |
| 5Sin(154t)
| 0,045
| 0,941
|
| -
|
| Ri
| |
| 56Cos(191t)
| 0,052
| 0,528
|
| -
|
| Ri
| |
| 36Sin(2t)
|
| 0,892
|
| -
|
| Ri
| |
| 214Cos(50t)
| 0,451
| -
|
|
|
| R2
| |
| 360Sin(10t)
| 0,912
| 9,95
|
| -
|
| Ri
| |
| 45Cos(25t)
| 12,7
| 0,132
|
| -
|
| Ri
| |
| 300Sin(2t)
| 9,82
| 20,13
|
|
|
| R2
| |
| 240Cos(11t)
| 12,6
| 0,628
|
| -
|
| Ri
| |
| 67Sin(17t)
| 54,1
| 0,063
|
|
|
| R2
| |
| 0,5Cos(88t)
| 9,17
| 0,0014
|
| -
|
| Ri
| |
| 16Sin(106t)
| 0,017
| 5,33
|
|
|
| Ri
| |
| 92Cos(89t)
| 0,729
| 0,174
|
| -
|
| Ri
| |
| 20Sin(14t)
| 0,527
| 9,24
|
| -
|
| Ri
| |
| 72Cos(71t)
| 0,332
| 0,59
|
| -
|
| Ri
| |
| 36Sin(20t)
| 0,375
| 8,26
|
| -
|
| Ri
| |
| Cos(36t)
| 0,108
| 7,09
|
| -
|
| Ri
| |
| 6Sin(42t)
| 0,085
| -
|
|
|
| Ri
| |
| 24Cos(23t)
| 0,188
|
|
| -
|
| Ri
| |
| 50Cos(30t)
| 0,051
| -
| 1,5
|
|
| R2
| |
| 3Sin(42t)
| 0,06
| 9,56
|
| -
|
| Ri
| |
| 24Cos(96t)
| 0,964
| 0,11
|
| -
|
| Ri
| |
| 12Sin(12t)
| 0,763
| 9,7
|
| -
|
| Ri
| |
| 4Cos(29t)
| 0,846
| -
|
|
|
| Ri
| |
| 36Sin(23t)
| 0,880
| 2,243
|
| -
|
| Ri
| |
| 120Cos(33t)
| 0,246
| 3,66
|
|
|
| R2
| |
| 110Sin(15t)
| 0,471
| 9,34
|
| -
|
| Ri
| |
| 240Cos(7t)
| 4,186
| -
|
|
|
| R2
| |
| 380Sin(4t)
| 8,258
| 8,127
|
| -
|
| Ri
| |
| 6Cos(4t)
| 9,716
| 7,128
|
| -
|
| Ri
| |
| 70Sin(10t)
| 4,816
| 2,112
|
| -
|
| Ri
| |
| 7Cos(10t)
| 1,128
| -
|
|
|
| R2
| |
| 220Sin(64t)
| 0,151
| 1,59
|
|
|
| R2
| |
| 89Cos(4t)
| 7,239
| 8,793
|
| -
|
| Ri
| |
| 34Sin(4t)
| 8,604
| -
|
|
|
| Ri
| |
| 214Cos(6t)
| 5,263
| 4,987
|
| -
|
| Ri
| |
| 360Sin(18t)
| 0,383
| 7,808
|
| -
|
| Ri
| |
| 78Cos(26t)
| 3,097
| 0,459
|
| -
|
| Ri
| |
| 54Sin(16t)
| 6,897
| 0,538
|
| -
|
| Ri
| |
| 65Cos(28t)
| 8,699
| -
|
|
|
| R2
| |
| 3Sin(29t)
| 5,637
| -
|
|
|
| Ri
| |
| 72Cos(11t)
| 9,841
| 8,02
|
| -
|
| Ri
| |
| 200Sin(2t)
| 34,17
| 7,477
|
|
|
| R2
| |
| 220Cos(46t)
| 2,780
| 0,17
|
|
|
| Ri
| |
| 350Sin(54t)
| 3,075
| 0,113
|
| -
|
| Ri
| |
| 18Cos(18t)
| 6,95
| 0,462
|
| -
|
| Ri
| |
| 36Sin(10t)
| 27,52
| 0,363
|
|
|
| R2
| |
| 23Sin(177t)
| 4,367
| 0,007
|
| -
|
| Ri
| |
| 67Cos(58t)
| 0,756
| -
|
|
|
| R2
| |
| 136Sin(47t)
| 5,139
| 0,087
|
| -
|
| Ri
| |
| 321Cos(19t)
| 3,714
| 0,718
|
| -
|
| Ri
| |
| 12Sin(4t)
| 37,22
| 1,733
|
|
|
| R2
| |
| 124Cos(18t)
| 4,037
| 0,8
|
| -
|
| Ri
| |
| 22Sin(117t)
| 1,248
| 0,006
|
|
|
| R2
| |
| 24Cos(9t)
| 22,56
| 0,578
|
| -
|
| Ri
| |
| 100Sin(15t)
| 6,022
| 0,775
|
| -
|
| Ri
|
Схемы для курсовой работы
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




