Вопрос 31. Теплопроводность. Закон Фурье. Коэффициент теплопроводности.
Теплопроводность - процесс передачи теплоты путем непосредственного соприкосновения тел, имеющих различную температуру. При этом процесс теплообмена происходит за счет передачи энергии микродвижения одних частиц другим.
Тепловой поток 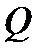 , , 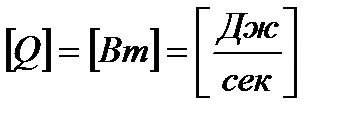 . .
Закон Фурье: тепловой поток пропорционален градиенту температуры и площади, то есть 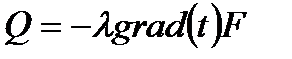 . .
Плотность теплового потока 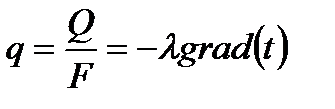 , , 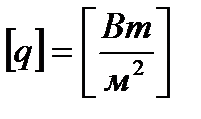 . .
Коэффициент теплопроводности 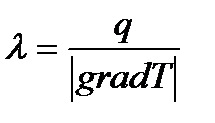 - количество теплоты, которое проходит в единицу времени через единицу поверхности через единичную толщину стенки при перепаде температуры в один градус, - количество теплоты, которое проходит в единицу времени через единицу поверхности через единичную толщину стенки при перепаде температуры в один градус, 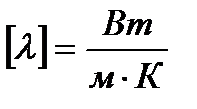 . .
_____________________________________________________________________
Вопрос 32. Дифференциальное уравнение теплопроводности. Условия однозначности.
Условности:
1. Теплофизические свойства системы: 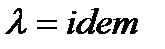 , , 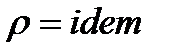 , ,  . .
2. Микрочастицы тела неподвижны.
3. Внутренние источники теплоты распределены в теле равномерно.
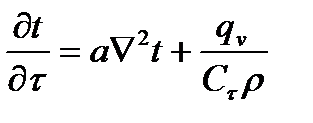 , где , где 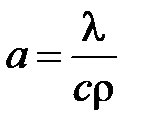 – коэффициент температуропроводности, характеризующий скорость изменения температуры в любой точке тела, [ – коэффициент температуропроводности, характеризующий скорость изменения температуры в любой точке тела, [ 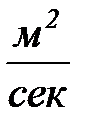 ] ]
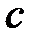 – теплоемкость тела; – теплоемкость тела; 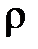 – плотность тела; – плотность тела;  – объемная плотность тепловыделения, [ вm/м3 ]; – объемная плотность тепловыделения, [ вm/м3 ]; 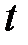 – температура; – температура;  – оператор Лапласа. – оператор Лапласа.
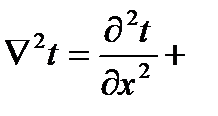 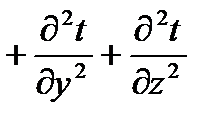 (для полярных координат (для полярных координат 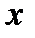 , , 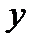 , , 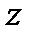 ), ),
Условия однозначности – математическое описание частных особенностей рассматриваемого процесса.
Решая уравнение 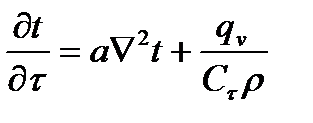 , получим общее решение, которое в совокупности с условиями однозначности даст нам частные решения. , получим общее решение, которое в совокупности с условиями однозначности даст нам частные решения.
Условия однозначности:
1. Геометрические условия (характеризуют форму, размеры и положение тела в пространстве):
a. Форма тела (плоское, цилиндрическое сферическое тело)
b. Ограниченное тело.
c. Неограниченное тело.
2. Физические условия (определяют физические свойства тела и среды)
a. Характер изменения физических параметров:
i. Характер изменения 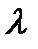 . .
ii. Характер изменения 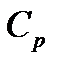 . .
iii. Характер изменения 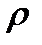 . .
iv. Характер изменения 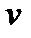 . .
3. Временные условия (дают представление о распределении температуры в исследуемом теле в начальный момент времени):
a. 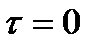 : :
i. 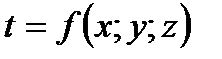 . .
ii. 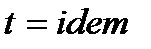 . .
b. 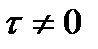 . .
4. Граничные условия (определяют особенности взаимодействия на границе изучаемого тела с окружающими телами (средой)):
a. Граничные условия первого рода – закон изменения температуры на границе тела:
i. 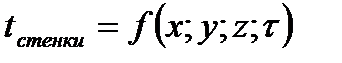 . .
ii. 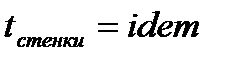 . .
b. Граничные условия второго рода – закон изменения температурного потока в стенке тела:
i. 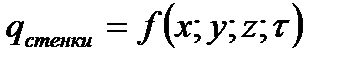 . .
ii. 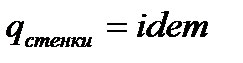 . .
c. Граничные условия третьего рода:
i. Закон изменения температуры окружающей среды.
ii. Закон, по которому идёт теплообмен тела с окружающей средой,  . .
d. Граничные условия четвёртого рода,  . .
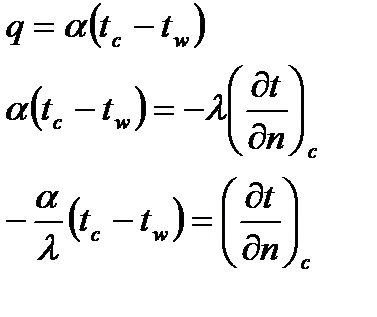    
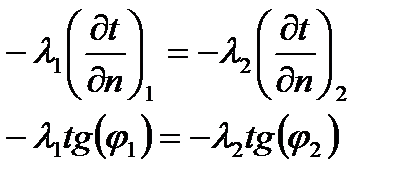
________________________________________________________
Билет 33. Теплопроводность через однослойные и многослойные плоские стенки.
Теплопроводность – процесс передачи теплоты соприкасающимися, беспорядочно движущимися структурными частицами вещества
В основу теории теплопроводности положен закон Фурье – тепловой поток прямо пропорционален температурному градиенту и площади поверхности тела. Закон Фурье для плоской однослойной стенки 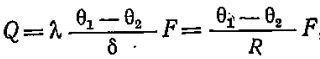

Плотность теплового потока – отношение теплового потока к площади поверхности теплопроводности. Для плоской стенки:
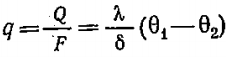 , где , где  . .
Коэффициент теплопроводности λ характеризует способность тел проводить теплоту.
Плотность теплового потока для стенки, состоящей из n слоёв:
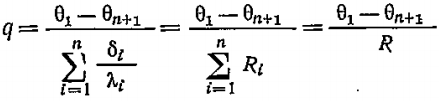 , ,
где R – термическое сопротивление многослойной стенки
Многослойную стенку можно заменить эквивалентной однослойной, толщина которой равна толщине многослойной стенки
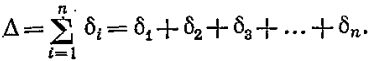
Тогда плотность теплового потока 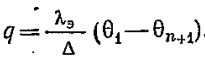 , где , где 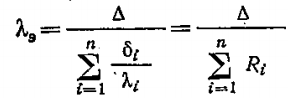
_____________________________________________________________________
Вопрос 34. Теплопроводность через однослойные и многослойные цилиндрические стенки
Тепловой поток для цилиндрической однослойной стенки:
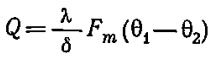
где Fm - расчётная поверхность теплопроводности,
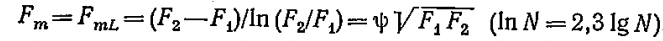
где...
δ – толщина стенки, δ=r2 – r1
F1, F2 – площади внутренней и наружной поверхностей трубы, [м2]
ψ – коэффициент, характеризующий отношение средней логарифмической FmL к средней геометрической 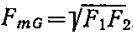
Линейная плотность теплового потока (тепловой поток, отнесённый к единице длины трубы) однослойной стенки определяется по формуле:
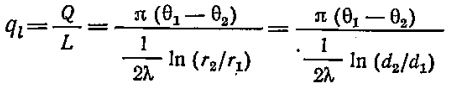
Тепловой поток для многослойной цилиндрической стенки:
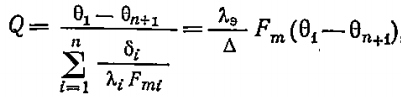
Где
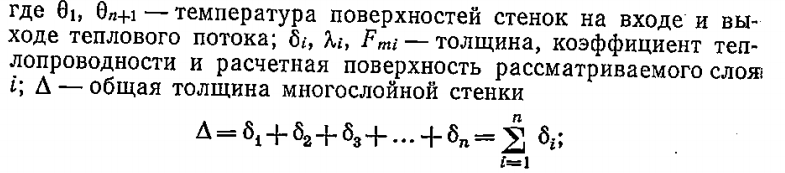
Fm – расчётная поверхность теплопроводности стенки;
λэ – эквивалентный коэффициент теплопроводности многослойной стенки
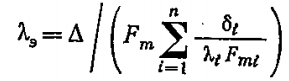
Линейная плотность теплового потока для многослойной стенки трубы
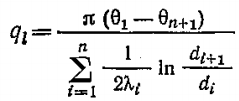
_____________________________________________________________________
Вопрос 35. Теплоотдача. Уравнение Ньютона. Коэффициент теплоотдачи.
Теплоотдача - конвективный теплообмен между жидкостью и поверхностью твёрдого тела (совместный перенос теплоты конвекцией и теплопроводностью).
Теплоотдачу рассчитывают по формуле Ньютона-Рихмана:
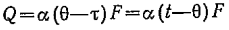
и плотность теплового потока
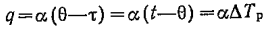

Коэффициент теплоотдачи зависит от: природы возникновения движения жидкости у поверхности теплообмена, режима движения жидкости, физических свойств жидкости, формы, размеров, положения в пространстве и состояния поверхности теплообмена.
____________________________________________________________________
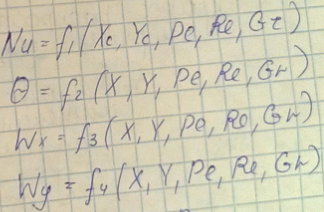 Вопрос 36. Критериальные уравнения, физический смысл критериев подобия. Числа подобия, составленные только из заданных величин математического описания задачи, называются определяющими критериями подобия. Критерии подобия, содержащие альфа, называются определяемыми. Вопрос 36. Критериальные уравнения, физический смысл критериев подобия. Числа подобия, составленные только из заданных величин математического описания задачи, называются определяющими критериями подобия. Критерии подобия, содержащие альфа, называются определяемыми.
Число Нуссельта, или критерий теплоотдачи, характеризует соотношение тепловых потоков, передаваемых конвекцией и теплопроводностью по нормали через пристенный слой.
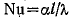 , где , где
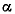 - коэффициент теплоотдачи, [Вт/м^2*С] - коэффициент теплоотдачи, [Вт/м^2*С]
l – определяющий линейный размер, [м]
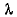 - коэффициент теплопроводности жидкости, [Вт/м**С] - коэффициент теплопроводности жидкости, [Вт/м**С]
Число Рейнольдса – критерий гидродинамического подобия, характеризуется соотношением сил инерции и молекулярного трения (вязкости)
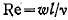 , где , где
w – средняя (линейная) скорость жидкости, определяется отношением объемного расхода к площади поперечного сечения потока, [м/с], 
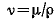 - кинематическая вязкость жидкости, [м^2/с] - кинематическая вязкость жидкости, [м^2/с]
По числовому значению Re судят о режиме течения жидкости:
Re<=2320 – ламинарный режим
Re>=10^4 – развитый турбулентный
2320<Re<10^4 – режим переходный
Число Прандтля характеризует физические свойства жидкости и их влияние на конвективный теплообмен. Число Прандтля определяет подобие температурных и скоростных полей в потоке жидкости.

, где альфа – коэффициент температуропроводности жидкости [м^2/с]
Число Пекле – критерий конвективного теплообмена, характеризует отношение плотности теплового потока, передаваемого конвекцией, к плотности теплового потока, передаваемого теплопроводностью
  Число Грасгофа характеризует соотношение подъемной силы, возникшей вследствие разности плотностей нагретых и холодных частиц жидкости и силы молекулярного трения, интенсивность свободного движения жидкости Число Грасгофа характеризует соотношение подъемной силы, возникшей вследствие разности плотностей нагретых и холодных частиц жидкости и силы молекулярного трения, интенсивность свободного движения жидкости

g – ускорение свободного падения, [м/с^2]
бета – температурный коэффициент объемного расширения
l – определяющий линейный размер
ϑ - разность между температурами жидкости и стенки
 — коэффициент кинематической вязкости [м²/с] — коэффициент кинематической вязкости [м²/с]
Установившийся конвективный теплообмен в общем случае описывается следующим уравнением подобия:

При вынужденном турбулентном движении:

Для чисто свободного движения:
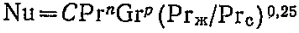
Введение множителя  даёт возможность использовать уравнение при любом направлении теплового потока (от стенки к среде и наоборот) даёт возможность использовать уравнение при любом направлении теплового потока (от стенки к среде и наоборот)
Теплоотдача при омывании плоской стенки:


_____________________________________________________________________
Вопрос 37. Последовательность расчетов конвективного теплообмена в условиях свободной конвекции.
Рассчитаем конвективный теплообмен на примере лабораторной работы

Дано:
Напряжение, подаваемое на опытную трубу U, [В]
Длина трубы l, [м]
Наружный диаметр трубы d, [м]
Температура окружающего воздуха tж, [°С]
Перепад температур между наружной поверхностью опытной трубы и окружающей средой, Δti=tci-tж, [°C] (данные шести термопар)
Обработка опытных данных начинается с определения теплового потока Q, передаваемого от опытной трубы в окружающую среду.
Соотношение для определения значения теплового потока Q в зависимости от напряжения U, подаваемого на опытную трубу, имеет следующий вид:

Средний перепад температур между наружной поверхностью опытной трубы и окружающей средой составляет

а средняя температура наружной поверхности опытной трубы равна

Средняя температура пограничного слоя воздуха у поверхности опыт-ной трубы равна
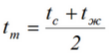
Теплота передается от наружной поверхности опытной трубы в окружа-ющую среду за счет конвективного и лучистого теплообмена. В условиях про-ведения контрольного опыта величина теплового потока, передаваемого от опытной трубы в окружающую среду путем излучения, составляет
 , где Co – излучательная способность абсолютно черного тела, равная 5,67 [Вт/м2К4], ε – степень черноты наружной поверхности опытной трубы, F – площадь наружной поверхности опытной трубы. , где Co – излучательная способность абсолютно черного тела, равная 5,67 [Вт/м2К4], ε – степень черноты наружной поверхности опытной трубы, F – площадь наружной поверхности опытной трубы.
Тепловой поток, передаваемый от опытной трубы в окружающую среду путем конвекции, равен
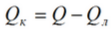
а опытное значение коэффициента теплоотдачи составляет
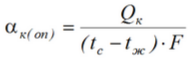
Определив при средней температуре пограничного слоя tm теплофизические свойства сухого воздуха λ; ν; β; Pr (находятся значения числа Грасгофа)
 и комплекса (GrPr). и комплекса (GrPr).
В зависимости от значения комплекса (GrPr) подбирается коэффициент C и показатель степени n в уравнении подобия конвективного теплообмена и определяются число Нуссельта
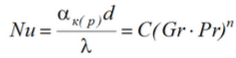
и расчетное значение коэффициента теплоотдачи
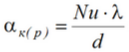
_____________________________________________________________________
Вопрос 38. Последовательность расчетов конвективного теплообмена в условиях вынужденной конвекции.
Рассчитаем конвективный теплообмен на примере лабораторной работы
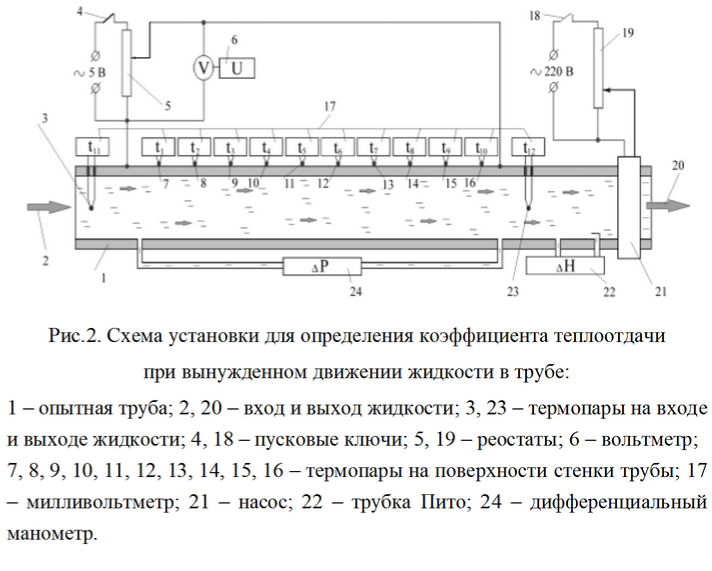
Дано: напряжение U [В]
Динамический напор жидкости ΔH [кГ/м2]
Температура стенки трубы t1 [°С] (10 измерений)
Температура жидкости на входе в трубу t11 [°C]
Температура жидкости на выходе из трубы t12 [°С]
Рассчитаем коэффициент теплоотдачи
Обработка опытных данных начинается с определения средней темпе-ратуры поверхности стенки трубы tс:
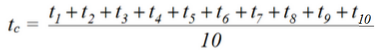
Средняя температура потока воды в трубе:
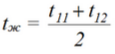
При средней температуре потока по таблице определяются теплофизические свойства воды: ρ; сp; λ; v.
Число Прандтля при средней температуре потока (10):
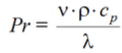
Скорость движения воды в трубе:
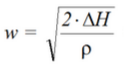
При движении жидкость нагревается на:
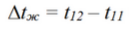
Количество теплоты в единицу времени, которое получает поток жид-кости от горячей поверхности стенки трубы:
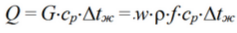
Плотность теплового потока от стенки трубы к потоку жидкости:
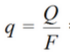
Опытное значение среднего коэффициента теплоотдачи:
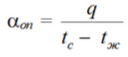
Число Рейнольдса (8) для потока жидкости в трубе:
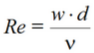
В зависимости от полученного значения определяется выражение для поиска числу Нуссельта.
Теоретическое значение среднего коэффициента теплоотдачи вычисляется из определения критерия Нуссельта
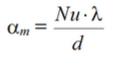
_____________________________________________________________________
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




