Характеристикой трубопровода называется график зависимости суммарных потерь напора в трубопроводе от расхода.

Для простого трубопровода потери равны требуемому напору, который в общем случае может быть найден по формуле

, (11.14)

которая при заданных значениях l, d, Σζ, однозначно отражает зависимость напора H от расхода Q.

Для квадратичной зоны сопротивления зависимость (11.13) переходит в следующую

, (11.15)

а если учитывать только сопротивления по длине, то (11.14) примет вид

. (11.16)

Зависимости (11.15) и (11.16) возможно представить в координатах H- Q, задавая ряд значений Q и определяя соответствующие значения Н. Построение графика зависимости Н от Q возможно в любой области сопротивления, а не только в квадратичной.

Полученная на рис. 11.3 кривая представляет геометрический образ характеристики трубопровода.

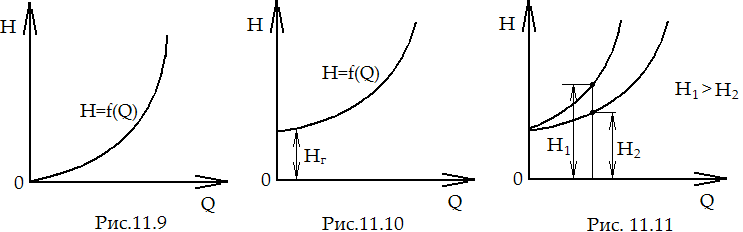
Рис. 11.3 Рис. 11.4 Рис. 11.5

Если помимо гидравлических сопротивлений необходимо еще преодолеть геометрический напор Н_г (высоту Н_г или эквивалентную разность давлений), то график (характеристика трубопровода) будет иметь вид, как на рис.11.4 (Н= Н_г при Q=0).

Допустим, что для данного трубопровода с открытым вентилем на нем построена зависимость Н от Q в виде графика 1 на рис. 11.5; если немного прикрыть этот вентиль на трубопроводе, то коэффициент его как местного сопротивления увеличится. При этом выражение в скобках в (11.14) также возрастет и при том же самом расходе потребуется больший напор, т.е. характеристика изменится и займет положение 2.

Последовательное и параллельное соединения

Трубопроводов

Последовательное соединение

Рассмотрим систему из последовательно соединенных труб различных диаметров и длин. Такое соединение участков трубопровода называется последовательным (рис. 11.9). Очевидно, что расход во всех последовательно соединенных трубах один и тот же, а полные потери напора Н для всего трубопровода равны сумме потерь напора на всех участках, т.е.

Q ₁= Q ₂= Q ₃ =…= Q _n = Q, (11.17)

H=H₁+H₂+ H₃+…+ H_n, (11.18)

где H₁, H₂, H₃, …, H_n – потери напора на 1, 2, 3, …, n -м участке.

Учитывая, что для каждого участка последовательного соединения справедлива зависимость (11.6) и имея в виду, что на каждом участке расход одинаковый, запишем (11.9) в виде:

. (11.19)

Из (11.19) следует, что решение первой и второй задач при последовательном соединении участков трубопровода разного диаметра будет таким же, как для простого трубопровода (трубопровода постоянного диаметра).

Третья же задача, если в ней потребовать определения диаметров для всех участков, становится неопределенной, так как в этом случае уравнение (11.19) содержит n неизвестных. Для решения этой задачи необходимо задать диаметры труб для всех участков, кроме одного, который может быть тогда определен.

Рис. 11.6 Рис. 11.7

Параллельное соединение

При параллельном соединении участков трубопровода жидкость, подходя с расходом Q к точке их разветвления А, распределяется по ответвлениям и далее снова собирается в точке их соединения В (рис. 11.7).

Заданы:

1. Суммарный расход до точки разветвления;

2. Длина, диаметр, величина к_э каждой ветви и все коэффициенты ζ_i

Найти:

1. Расходы Q₁, Q₂, Q₃, …, Q_n на отдельных участках, соединенных параллельно (в параллельных ветвях)

2. Потери напора Δ h между точками А и В на каждом участке.

При решении задачи, прежде всего, учтем очевидный факт:

равенство расхода Q сумме всех расходов

Q = Q₁ + Q₂ + Q₃ + … + Q_n. (11.20)

Для дальнейшего решения представим, что в точках А и В установлены пьезометры; так как концы всех трубопроводов смыкаются в одних и тех же точках А и В, то потери на всех этих участках одинаковы и равны Δ h (Δ h - разность показаний пьезометров, установленных в точках А и В).Поэтому справедливы следующие равенства

Δ h= Δ h₁= Δ h₂= Δ h₃= …= Δ h_n. (11.21)

Решение задачи выполним методом характеристик.

Для решения на графике ∆h-Q строится (по 4-6 точкам) характеристики первой, второй и третьей ветвей, рис 11.8.

Каждая точка на графике получением заданием расхода Q_i и подстановкой его в уравнение

Далее при нескольких произвольных значениях ∆h суммируются расходы для всех 3-х ветвей и, таким образом, получается суммарная кривая S. Она по своему смыслу выражает зависимость потерь ∆h от суммарного (общего) расхода Q. Но общий расход Q задан, поэтому откладывают его значение на горизонтальной оси, восстанавливают из этой точки перпендикуляр до пересечения с кривой S и находят на вертикальной оси соответствующее значение ∆h (расходы в ветвях находят по точкам пересечения горизонтальной прямой А-В с характеристиками ветвей).

Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? - задался я вопросом...

Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем...

Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор...

Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: