|
|
Метод деления отрезка пополам.
Общие сведения Постановка задачи. Пусть дана некоторая функция f(x). Необходимо найти с точностью до e такое x*, что f(x*)=0. В том случае, когда решение не может быть найдено в явном виде, применяются численные методы. Наиболее распространенными из них являются метод деления отрезка пополам, метод простых итераций, метод касательных (Ньютона), метод секущих и метод хорд.
Рассмотрим метод деления отрезка пополам более подробно. В соответствии с этим методом вначале необходимо приблизительно определить отрезок, на котором функция f(x) меняет знак. Для этого можно использовать графический способ, заключающийся в построении графика функции на экране компьютера и приблизительного визуального определения точек пересечения графика с осью абсцисс.
Блок-схема алгоритма поиска корня уравнения f(x)=0 Методом деления отрезка пополам
Метод хорд.
Является более быстрым способом нахождения корня уравнения f(x)=0 лежащего на отрезке [a;b], таком, что f(a)*f(b)<0. Для определённости пусть f(x)<0, f(b)>0. Разделим отрезок в отношении -f(a)/f(b). Это даёт приближённое значение корня x1=a+h1, где h1=-f(a)*(b-a)/(-f(a)+f(b)). Применяя этот приём, к тому из отрезков [a;x1] или [x1;b] на концах которого функция имеет противоположные знаки. Получим второе приближение корня x2. Геометрически, метод хорд эквивалентен замене кривой y=f(x) хордой проходящей через т. а и т. B. Уравнение хорды: (x-a)/(b-a)=(y-f(a))/(f(b)-f(a)). Полагая, что х=х1 и у=0, получим х1=а - f(a)*(b-a)/(f(b)-f(a)), x1 – первое приближение. Для сходимости процессов корень должен быть отделён вторая производная должна сохранять знак на отрезке [a;b]. Процесс вычисления заканчивается когда разность между 2-мя значениями корня <e или |f(xn+1)|<e. Графическая интерпретация показана на рис.
f(b) a=xo b
x f(a)
Блок-схема алгоритма поиска корня уравнения f(x)=0
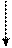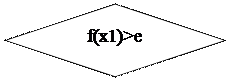        методом хорд
Метод простой итерации.
Метод простой итерации используется для решения нелинейных уравнений. Метод основан на последовательном приближении к корню уравнения при заданных начальных условиях: начальное приближение и точность вычисления. При использовании метода простой итерации, важным является выбор функции х = F(x), при этом должно выполняться условие: │f(x)│< q < 1 (f(x) – производная функции F(x)) во всех точках интервала изоляции [а;b] - это необходимое условие сходимости процесса. Преобразование исходного уравнения к виду х=F(x) можно осуществить многими методами. Например, выделить х из исходного уравнения, а остальное перевести в правую часть.Вычисления заканчиваются когда │xn+1 - xn│< ε. Алгоритм нахождения корня: 1) Заменяем уравнения f(x)=0 выражением x=φ(x) 2) Находим х1= φ(xо). 3) Проверяем |x1-xo|<=e, если выполняется условие, х1-корень, если нет,продолжаем: х2= φ(x1) x3= φ(x2) …….. xn+1 = φ(xn) Счет заканчивается, когда | xn+1 - xn | <=e либо f(xn+1)<=e. Условие, при котором данный процесс сходится, определяется следующей теоремой: если интервал [a,b] является интервалом изоляции корня уравнения x = φ(x), и во всех точках этого интервала производная φ’(x) удовлетворяет условию: |φ’(xn)|<q<1 то итерационный процесс сходиться. В случае, если по условию | xn+1 - xn | <=e невозможно найти корень, то заданную точность вычислений необходимо найти из выражения, где q- наименьшее значение |φ’(x)| на отрезке [a,b].
| xn+1 - xn | <=(1-q)*e/q Таким образом начальное приближение выбирается из соображений |φ’(xо)|<1. При использовании метода простой итерации важным является выбор функций φ(x). Ее производная должна удовлетворять условию сходимости. При этом скорость сходимости тем выше, чем ниже q. Преобразование исходного уравнения к виду x=φ(x) может осуществляться многими методами, например выделить х из уравнения f(x) =0, а остальное перенести в правую часть.
Блок-схема алгоритма поиска корня уравнения f(x)=0
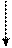  методом простой итерации
Метод Ньютона Метод Ньютона используется для решения нелинейных уравнений. Метод основан на последовательном приближении к корню уравнения при заданных начальных условиях: начальное приближение и точность вычисления. В методе Ньютона осуществляется экстерполяция с помощью касательной к кривой в данной точке. В основе метода лежит разложение функции по формуле Тейлора. Члены, содержащие h во второй и более высоких степенях, отбрасываются. Для нахождения корня используется соотношение xn+1 = xn + h. Предполагается, что переход от xn к xn+1 приближает значение функции к нулю. h = -f(x)/f’(x) тогда xn+1 = xn - -f(x)/f’(x) Геометрически метод Ньютона эквивалентен замене небольшой дуги y=f(x) касательной, проведенной в некоторой точке кривой.
y f(b)
b 0 a x3 x2 x1 x f(a)
Блок-схема алгоритма поиска корня уравнения f(x)=0 Методом Ньютона
Нет
да
да
нет
Метод Гауса. При численном решении систем линейных уравнений одним из распространенных является метод Гаусса, сущность которого сводится к поэтапному исключению неизвестных из уравнений. Исходная матрица: а11*v+а12*z=d1 а21*v+а22*z=d2 1) если а11<>0, то разделим первое уравнение на а11 и умножим на а21. Вычтем из второго уравнения преобразованное первое. Получим: (а22-а12/a11)*z=(d2-d1/a11) откуда z2=d*/a*,где d*= d2-d1/a11 a*= а22-а12/a11 Сейчас легко находим v: v=d1/а11-v*а12/a11. Аналогично для матриц большего порядка. Метод итерации. При большом числе неизвестных используют приближённо-численные методы. Дана СЛАУ: а11*х1+а12*х2+…+х1n*хn=В1 а21*х1+а22*х2+…+х2n*xn=B2 ….. an1*x1+an2*x2+…+ann*xn=Bn
|a11 a12 … a1n| |B1| |x1| A=| a21 a22 … a2n| B= |B2 x=|x2| |…. | |….| |…| |an1 an2 … ann| |Bn| |xn| Предположим, что аii<>0. Разрешим первое уравнение относительно х1, второе относительно х2 и т.д. x1=b1+A12*x2 +A13*x2+…+A1n*xn x2=b2+A21*x1+A23*x3+…+A2n*xn ….. xn=bn+An1*x1+An2*x2+…+An(n-1)*n(n-1)
Тогда x=b + A*x Далее решаем методом последовательных приближений. За начальное приближение выбираем столбец свободных членов: X10=b1 X20=b1 ….. Xn0=b1; Алгоритм нахождения корней: X11=b1+A*x10 X21=b2+A*x20 ….. Xn1=bn+A*xn0
Вычисление заканчивается тогда, когда разность между 2-мя ближними итерациями значений корня будет <=e.
Метод Зейделя. Он представляет собой некоторую модификацию метода итерации. основная идея в том, что при вычислении к+1 приближения неизвестных xi учитываются уже вычисленные к+1 значения переменной x1,x2,x3,… Метод Зейделя даёт лучшую сходимость, чем метод итерации, но приводит к более громоздким вычислениям. Этот метод может сходиться тогда, когда метод итерации расходится, и наоборот, процесс заканчивается когда разность приближёния корня в соседней итерации <= заданной точности.
Метод Горнера. Существует много методов для решения полиномов на языке PASCAL. Один из этих методов – разложение полинома по схеме Горнера. Полином f(x) = a0 + a1t + + a2t2+ a3t3+ a4t4+ … + antn по схеме Горнера представляется в виде f(x) = a0 + t(a1 + t(a2 +t(a3 +… + t(an-1 + t an)…)))
Данное разложение полинома удобно тем, что в нём отсутствует возведение в степень, что значительно ускоряет вычисление полинома.
  Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам...  ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования...  Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...  ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|
При отыскании корня методом половинного деления сначала вычисляются значения функции в точках a и b - соответственно f(a) и f(b), имеющие противоположные знаки. Далее по формуле xср=(a+b)/2 вычисляется координата центра отрезка [a, b] и находится значение функции в этой точке f(xср). Оно сравнивается со значениями функции на концах отрезка. Если функция меняет знак на отрезке [a, xср], то весь отрезок [a, b] усекается до его левой части, то есть xср становится правой границей отрезка (b). Аналогично, если функция меняет знак на отрезке [xср, b], отрезок [a, b] усекается до правой части. Эти операции повторяются до тех пор, пока разница между соседними значениями x не станет меньше или равной выбранной точности.
f(x)
0 x1 x2 x*
нет
да