Сдам Сам
Главная | Контакты | FAQ

ПОЛЕЗНОЕ
Как развить коммуникабельность Почему могут возникнуть ссоры между супругами, в то время как их отношения кажутся прочными Почему появляется страх? Как стать богатым и отойти от дел молодым Советы от доктора Айболита «Как быть здоровым» Как сделать приглашение правильно Точка зрения. Как сделать сотрудника вовлеченным? Лень и как с ней бороться. Психологические аспекты Способов заработать с помощью internet Лекции по Основам предпринимательства Последнее добавление


КАТЕГОРИИ
АвтоматизацияАрхитектураАстрономияАудит Биология Бухгалтерия Генетика География Геология Изобретательство Информатика Искусство История Компьютеры Литература Логика Маркетинг МатематикаМашиностроение Медицина Менеджмент Металлы и Сварка Механика Образование Педагогика Политика ПравоотношениеПроизводство Психология РазноеРелигия Социология Спорт Технологии Торговля Физика Философия Финансы Химия Экология Экономика







РОЗВ’ЯЗАННЯ СИСТЕМИ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ МЕТОДОМ ГАУССА





 

 

Задана система лінійних алгебраїчних рівнянь

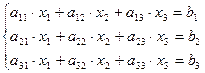
Числові значення коефіцієнтів системи наведені в таблиці 15.1.

Для розв’язання системи рівнянь необхідно:

- скласти графічний алгоритм визначення коренів системи;

- скласти програму для ЕОМ або скористатися стандартною підпрограмою;

- розв’язати систему рівнянь в діалоговому режимі;

- провести аналіз результатів.

 

РОЗВ’ЯЗАННЯ СИСТЕМИ АЛГЕБРАЇЧНИХ РІВНЯНЬ МЕТОДОМ ПРОСТОЇ ІТЕРАЦІЇ АБО МЕТОДОМ ЗЕЙЛЯ

Для розв’язання рівнянь необхідно:

-скласти графічний алгоритм знаходження коренів системи рівнянь з точністю до 0.01;

-скласти програму для ЕОМ або скористатися стандартною підпрограмою;

-розв’язати систему в діалоговому режимі;

-провести аналіз результатів.

Систему рівнянь та варіанти завдань взяти з таблиці 15.1. Метод розв’язання вказує викладач.

Таблиця 15.1-Варіанти завдань

    Коефіцієнти системи
N вар і аі1 аі2 аі3 bi

 

           
  1 2 3 0.10 0.12 -0.13 0.12 0.71 0.15 -0.13 0.15 0.63 0.10 0.26 0.38
  1 2 3 0.34 -0.04 0.10 -0.04 0.10 0.12 0.10 0.12 0.71 0.33 -0.05 0.28
  1 2 3 0.63 0.05 0.15 0.05 0.34 0.10 0.15 0.10 0.71 0.34 0.32 0.42
  1 2 3 0.30 -0.10 -1.5 1.20 -0.20 -0.30 0.15 0.10 0.71 0.34 0.32 0.42
  1 2 3 6.36 7.42 5.77 11.75 19.03 7.42 11.75 6.36 -41.70 -49.49 -27.67
  1 2 3 0.103 0.047 -0.167 0.012 0.809 -0.106 0.075 -0.142 -1.109 1.209 0.914 0.649
  1 2 3 0.894 -0.191 0.062 0.0 0.872 0.021 0.047 0.196 -1.086 0.941 -1.425 1.113
  1 2 3 0.868 0.093 0.135 0.102 0.943 -0.069 -0.132 0.120 0.909 0.787 1.395 1.483
  1 2 3 1.035 -0.194 -0.002 0.120 1.098 0.089 0.137 -0.173 -0.962 -0.947 -1.181 -0.91
  1 2 3 -0.934 0.076 -0.149 0.08 0.841 -0.074 0.083 -0.159 -0.787 1.107 0.688 -0.932
  1 2 3 -0.969 0.164 0.106 0.169 1.006 -0.155 -0.002 -0.164 0.954 -0.633 -0.693 -1.113
  1 2 3 -0.095 0.0 0.111 0.192 -0.169 -0.083 -0.6 -0.199 0.813 1.359 -1.153 0.635
  1 2 3 0.71 0.1 0.12 0.1 0.34 -0.04 0.12 -0.04 0.1 0.29 0.32 -0.1
  1 2 3 0.1 -0.04 -0.13 -0.04 0.34 -0.04 -0.13 0.05 0.63 -0.15 0.31 0.37
  1 2 3 1.2 -0.2 -0.3 -0.2 1.6 0.1 0.3 -0.1 -1.5 -0.6 0.3 0.4
  1 2 3 0.2 0.58 0.05 0.44 -0.29 0.34 0.81 0.05 0.1 0.74 0.02 0.32
  1 2 3 3.11 -1.65 0.6 -1.66 3.51 0.78 -0.6 -0.78 -1.87 -0.92 2.57 1.65
  1 2 3 1.11 0.111 -0.123 -0.199 -0.903 -0.164 0.049 0.196 0.98 -1.26 -0.677 1.015
  1 2 3 0.818 0.161 0.008 0.196 1.083 -0.055 0.074 0.021 1.023 1.053 1.145 1.104
  1 2 3 1.008 0.134 -0.133 -0.137 1.071 0.071 -0.055 0.015 -0.934 1.269 -0.796 1.332
  1 2 3 0.908 0.061 -0.16 0.024 0.872 0.103 0.025 -0.087 -1.138 -0.786 0.752 1.332
  1 2 3 0.828 0.161 0.188 0.061 1.085 0.069 0.106 -0.055 0.922 -0.898 -1.425 0.625
  1 2 3 -0.816 0.075 -0.199 0.025 1.111 -0.097 0.125 -0.05 1.02 0.777 -1.301 -0.813
  1 2 3 0.73 1.12 0.32 -0.85 -0.14 0.23 1.08 0.51 -0.49 0.67 0.83 0.17
  1 2 3 1.421 -2.05 1.09 -2.15 0.77 -2.21 1.1 -2.03 1.41 0.69 1.03 1.35

 

ЧИСЛОВЕ ІНТЕГРУВАННЯ

 

За варіантами завдань, наведених в таблиці 16.1, обчислити означений інтеграл f(x)dx із заданою похибкою,поділивши проміжок [a,b] на n частин, для цього потрібно:

-скласти графічний алгоритм;

-написати програму або скористатися стандартною;

-розв’язати задачу на ЕОМ в діалоговому режимі.

 

Таблиця 16.1 –Варіанти завдань

N вар Підінтегральна Функція n a b   Метод розв`язування

 

             
  1/(sqr(2*x3+1.5))   0.8 0.6 0.001 Прямокутникiв
  sqr(1-2.7*x3)   0.1 1.5 0.001 Трапецiй
  x/ln(x)       0.001 Сiмпсона
  1/sqr(4*x2+1.5)   0.6 1.7 0.001 Прямокутникiв
  sqr(1.5-0.4*tg(x2))   1.5 2.1 0.001 Трапецiй
  x*arctg(x)/3Ö(1+x3)   0.2 2.1 0.001 Ciмпсона
  (p-x2)*sin(3Ö(2.1+x)       0.001 Прямокутникiв
  x*sqr(cos(x))   0.1 1.1 0.001 Трапецiй
  1/sqr(1.8*x2+0.7)   1.2 2.4 0.001 Ciмпсона
  cos(x)/(1+ln2(x))   2.3 3.6 0.001 Прямокутникiв
  sin(x)/x   0.7 1.7 0.001 Трапецiй
  ln(x)*cos(x+0.8)   1.3 2.7 0.001 Ciмпсона
  sqr(1-1/4*sin2(x))     1.6 0.001 Прямокутникiв
  sqr(1+x)/ln(x)       0.001 Трапецiй
  tg2(x)+ctg2(x)   p/6 p/3 0.001 Сiмпсона
      1.5 0.001 прямокутникiв
  x*ex*sin(x)       0.001 трапецiй
  sqr(1+x4)   0.1 1.6 0.001 Сiмпсона
  sqr(x)*sin(x)   0.2 1.6 0.001 прямокутникiв
  xx*(1+ln(x))       0.001 трапецiй
Продовження таблиці 16.1
21

 ln2(x)/x       0.001 Сiмпсона
  x*arctg(x)       0.001 прямокутникiв
  ex*cos2(x)     п 0.001 трапецiй
  sin(x)*ln(tg(x))     1.5 0.001 Сiмпсона
  x3/(3+x)       0.001 трапецiй

РОЗВЯЗАННЯ ДИФЕРЕНЦІЙНИХ

РIВНЯНЬ

Одержати числовий розв'язок диферeнцiйного рівняння вiдповiдним методом(Ейлера, Ейлера-Кошi,Рунге-Кутта) при заданих початкових умовах на вказаному iнтервалi. Для цього необхiдно:

-скласти графiчний алгоритм;

-розробити програму або скористатися стандартною;

-розв'язати рiвняння на ЕОМ в дiалоговому режимi;

-проаналiзувати результат наближеного розв'язку рiвняння.

Варiанти завдань наведенi в таблицi 16.1.

 

ІНТЕРПОЛЯЦІЯ ФУНКЦІЙ

Необхідно побудувати інтерполяційну залежність, яка у вузлах інтерполяції набуває тих же значень, що і функція, яка задана таблично, користуючись поліномом Лагранжа або многочленом Ньютона. Для цього потрібно:

- скласти графічний алгоритм обчислення значення функції у=f(x) при заданому значенні аргумента х;

- розробити програму і розв’язати задачу на ЕОМ;

- проаналізувати результат обчислення.

Вихідні дані наведені в таблиці 18.1.

Таблиця 18.1- Варіанти завдань

Номер варіанту   Вузли інтерполяції Значення аргумента
                 
                 

 

                 
  x y 0.41 1.821 0.72 2.735 1.0 3.908 1.32 5.756 1.61 6.756 1.85 8.631 1.21
  x y 3.63 12.423 4.20 10.612 4.72 8.216 5.01 7.421 5.53 5.603 5.91 3.805 3.89
  x y 5 19.21 8 31.12 11 50.35 14 42.61 17 38.44 19 31.72 10.61
  x y 0.36 2.652 0.53 3.06 0.96 3.898 0.92 4.917 1.16 5.814 1.28 7.213 0.66
  x y 1.68 0.8071 1.73 0.899 1.82 1.2036 1.88 1.2615 1.96 0.9871 2.02 0.7815 1.79
  x y 0.3 1.422 0.6 2.6781 0.9 3.071 1.2 4.4115 1.5 6.0871 1.8 7.953 1.15
  x y -0.33 6.812 -0.52 6.812 -0.84 9.106 -1.23 11.21 -1.52 12.631 -1.91 11.853 -1.65
  x y 0.4 -2.149 0.2 -0.61 0.06 1.806 -0.21 2.512 -0.46 3.261 -0.71 4.121 0.16
  x y 0.55 1.316 0.72 2.481 0.88 3.781 1.06 3.605 1.14 2.261 1.48 1.561 1.23
  x y -0.45 1.561 -0.84 2.935 -1.13 5.621 -1.42 9.806 -1.76 13.643 -2.1 18.256 -1.69
  x y 1.4 2.561 1.6 2.089 1.8 1.863 1 2.612 1.2 2.612 1.4 3.126 1.72
  x y 2.3 6.306 2.7 4.287 3.0 2.145 3.41 0.631 3.6 -3.615 4.8 -5.861 5.62
  x y 1.35 12.75 1.41 11.653 1.48 8.35 1.56 6.36 1.59 3.81 2.01 1.81 1.79
  x y 2.75 2.361 1.653 2.523 0.835 2.572 0.636 2.791 0.385 3.012 0.182 3.689 2.42
  x y 3.5 2.721 4.1 2.306 4.6 1.931 5.2 1.801 5.7 1.571 5.4 1.326 4.92
  x y 0.65 12.413 0.41 11.243 0.48 16.851 0.52 20.321 0.61 14.351 0.78 16.821 0.631
  x y 0.46 2.401 0.49 2.261 0.56 2.061 0.63 1.901 0.72 1.621 0.79 1.391 0.61
Продовження таблиці 18.1
18

 x y 3.69 -0.023 9.28 0.084 13.17 0.125 17.36 0.176 19.25 0.227 1.64 -0.06 10.65
  x y 2.143 8.369 2.654 9.471 3.265 8.182 3.676 7.093 4.287 6.124 4.287 6.124 3.75
  x y 1.82 0.806 2.735 0.917 3.9 1.068 5.42 1.219 6.76 1.352 8.65 1.423 4.52
  x y -0.3 -3.154 -0.16 -1.965 0.04 -0.526 0.23 2.187 0.4 3.658 0.61 6.019 -0.26
  x y -0.85 5.235 -1.26 7.444 -1.67 9.353 -2.18 6.162 -2.39 5.67 -2.71 3.881 -1.95
  x y 0.4 1.256 0.8 2.475 1.2 4.574 1.6 8.183 2.0 9.392 2.4 11.601 1.78
  x y 1.5 1.882 1.9 2.773 1.3 4.464 1.7 6.355 2.1 8.746 2.5 11.237 1.45
  x y 6.8 11.412 7.5 10.621 9.1 8.23 11.2 11.349 12.6 13.858 11.85 17.367 10.36

 







Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все...

Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...

ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между...

ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала...




Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

©2015- 2025 zdamsam.ru Размещенные материалы защищены законодательством РФ.