|
|
Увеличением количества испытаний.Величина, около которой происходит стабилизация относительной частоты случайного события как раз и характеризует его вероятность. Нередко в свой речи мы выражаем интуитивное понимание вероятности реализации той или иной ситуации формулировками типа “шансы пятьдесят на пятьдесят” или “девять против одного”. Теория вероятностей поднимает тему случайности до уровня серьезной и строгой науки. 2.4. Множество событий и операции на нем В каждом конкретном случайном эксперименте случайные события образуют множество, на котором могут быть введены различные операции, позволяющие из простейших событий формировать сложные события. В дальнейшем, следуя традиции, случайные события как элементы соответствующего множества будут обозначаться прописными латинскими буквами, а когда это будет удобно, то и русскими. Словесное описание содержания события раскрывается с помощью знака равенства, который в данной ситуации читается как “состоит в том, что”. Например, запись А=“выпал орел” может быть прочитана как написано и означает, что содержанием события А является выпадение орла при бросании монеты. Первой в списке операций логично поставить сравнение событий. Если событие В происходит всегда, когда произошло событие А, то говорят что из А следует В и обозначают символом АÌВ. Например, если при бросании кубика А=”выпала цифра 2’’ и В=”выпало четное число”, то АÌВ. Однако в данной ситуации очевидно из В не следует А, т.е. ВËА. Таким образом все случайные события относительно друг друга находятся в отношении следствия с ответом “да” или “нет”. Теперь можно сформулировать условие равенства событий. События А и В называются равными, если из А следует В и наоборот, т.е. АÌВ и ВÌА Û А=В. Например, если при бросании кубика А=”выпало четное число”, а В=”выпало или 2 или 4 или 6”, то А=В. Суммой двух событий называется событие А+В, которое состоит в том, что произошло событие или А или В или оба одновременно. Здесь “одновременно” не просто слово, а термин, понимаемый не буквально как реализация событий физически в один момент времени, а в смысле “вместе”. В этом определении “или” имеет не исключающий характер, поскольку допускает совместное возникновение событий. Если в эксперименте со стрельбой
Из определения суммы событий следует, что она обладает свойствами коммутативности (перестановочности слагаемых) А+В=В+А и ассоциативности (возможности изменения порядка суммирования) А+(В+С)=(А+В)+С. Очевидно, что АÌА+В "В, а также А+А=А. Последний результат свидетельствует о принципиальном отличии алгебры событий от привычной алгебры чисел. Упражнение. При бросании кубика представить случайное событие А=”выпало четное число” в виде суммы событий его составляющих, введя соответствующие обозначения.
 = “попадание в первом выстреле”, а = “попадание в первом выстреле”, а 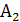 =”попадание во втором выстреле” попадание дважды будет являться произведением этих событий, т.е. =”попадание во втором выстреле” попадание дважды будет являться произведением этих событий, т.е. 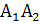 =”попасть дважды”. =”попасть дважды”.
В соответствии содержанием операции произведения событий АА=А. Умножение событий коммутативно (сомножители можно менять местами) АВ= ВА, ассоциативно (сомножители можно группировать в указанном порядке) А(ВС)=(АВ)С и дистрибутивно (можно раскрывать скобки и выносить общий множитель за скобки) А(В+С)=АВ+АС. Скобки, как и обычно, устанавливают приоритет операций. Рассмотренныеоперации над событиямив частностиимеют своими следствиями: АÉ АВÌВ,А+АВ=А при любом В как сумма события фактически с самим собой, в чем нетрудно убедиться с помощью кругов Эйлера. Особенности алгебры событий проявляются в таком примере (А+В)(А+С)=АА+АС+ВА+ВС=(А+АВ)+АС+ВС=А+АС+ВС=(А+АС)+ВС=А+ВС. Упражнение. Доказать полученный результат непосредственно с помощью кругов Эйлера для всех трех событий А, В и С.   Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...  ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между...  Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот...  ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|