|
|
Оценка вероятности промаха БП типа кэш.Стр 1 из 3Следующая ⇒ Лекция №1. Введение. При разработке вычислительных машин (ВМ) и систем необходимо решить множество вопросов: «Каким должен быть объем буферной памяти (БП)? Как должна быть реализована сама БП?» и т.д. Существуют три пути решения этих вопросов. Первый путь основан на опыте разработчиков, но это означает, что мы можем получить не совсем оптимальное решение. Второй путь основан на некоторой модификации реально существующей системы. Третий путь основан на моделировании, которое бывает имитационное (используется специальный язык программирования) и аналитическое (создаются математические модели процессов, которые происходят в ВМ).
Моделирование БП типа кэш. При изучении тракта оперативная память (ОП) - БП - центральный процессор (ЦП) нужно решить: какой способ отображения использовать, размер блока, количество блоков, алгоритм замещения, дисциплина обновления ОП. В качестве критериев оптимальности могут быть использованы разные показатели. Например, время выполнения команды, программы, объем оборудования. Рассмотрим первый критерий. При выполнении команды существует несколько этапов ее выполнения, на каждом из которых тратится время. Нас интересуют этапы, связанные с обращениями к ОП. При выполнении команды может произойти не одно обращение к памяти. Рассмотрим этап, связанный с выборкой команды. Для простоты будем считать, что время выполнения команды и будет выборка ее из памяти. За командой мы сначала обращаемся к БП. Но при этом может быть «успех» или «неуспех». Введем частоту (вероятность) «неуспеха» P, тогда с вероятностью 1-Р время выборки команды равно времени обращения к БП (ТБП), а с вероятность Р время выборки команды равно сумме времен обращения к БП и ОП (ТБП+ТОП) следовательно, можно найти средне время выполнения команды: Т=(1-Р)*ТБП+Р*(ТБП+ТОП)=ТБП+Р*ТОП Определение. Обратная величина (1/Т) называется производительностью. Она показывает, сколько команд выполняется в единицу времени. ПР=1/Т=1/ ТБП+Р*ТОП
При увеличении вероятности «неуспеха» происходит резкое падение производительности. Оценим его: пусть ТБП=1; ТОП=10; Р=0.1, то ПР=1/2*ТБП - уменьшилась в два раза, следовательно, от вероятности промаха зависит производительность. Рассмотрим параметры, которые оказывают влияние на вероятность промаха. Если это влияние слабое, тогда параметр является несущественным и при моделировании его можно исключить. Если же наоборот, то этот параметр - существенный и носит название атрибут.
Структурированный подход.
При создании модели этого тракта необходимо рассмотреть две модели: модель работы БП и модель работы рабочей нагрузки. Во время выполнения программы происходит обращение за командами или за данными. В связи с этим можно говорить, что существует поток команд и данных или говорят, что существует рабочая нагрузка. Нас интересует адресная трасса - номера ячеек, к которым происходит обращение, следовательно, существует проблема задания адресной трассы при моделировании тракта ОП - БП - ЦП. Адресную трассу можно задать, используя структурированный подход. Все операторы можно разбить на следующие классы: - операторы следования; - операторы перехода; - операторы цикла. Существует доказательство, что все операторы могут быть сведены к выше перечисленным операторам. В результате получим, что адресная трасса примет вид: (i,i+1), если i-ый оператор является оператором следования; (i,i+k), если i-ый оператор - безусловный переход вперед; (i,..,i+l,i,...,i+l,...,i,...,i+l) (r раз), если i-ый оператор - оператор цикла. Получившаяся рабочая нагрузка обусловлена только наличием команд. Реальная программа состоит из комбинации этих объектов.
Лекция №2 Лекция №3
Секторное отображение.
Пусть V-объем БП, S-число секторов. Алгоритм замещения LRU.
ДЗ. Доказать, что для FIFO будет аналогично.
Оптимальный алгоритм замещения для группо-ассоциативного Отображения.
РИСУНОК ДЗ. Найти вероятность промаха для группо-ассоциативного отображения для произвольного Т.
Лекция №4. Алгоритм замещения LRU.
Пусть БП имеет чисто ассоциативное отображение, следовательно имеется V=S мест. Для того чтобы описать состояние БП типа кэш необходимо использовать вектор длиной S, и элементы этого вектора есть номера блоков, которые находятся в кэш. Пусть блоки в векторе располагаются по принципу: слева - самый «молодой», а справа - самый «старый». Например пусть для S=4 вектор будет 5,3,7,8. Тогда самый «молодой» будет блок с номером 5, а самый «старый» - 8.
Пусть S=2, n=3. Построим граф переходных вероятностей, у которого число состояний - это число размещений n по S.
ДЗ. Достроить граф. Найдем вероятность
А вероятность промаха будет:
В общем случае
ДЗ. S=3, n=6. Найти Мы имеем систему Выразим из системы все
Двоичное дерево. Пусть n-произвольное, S=8.
ДЗ. 1) S=8,n=12. 2) Построить граф переходов для а) равновероятного алгоритма замещения; б) алгоритма замещения FIFO.
Лекция №5. Дискретное распределение.
Определим состояние системы тремя параметрами U1U2U3, где U1 - указывает сколько времени осталось до завершения считывания команды из ОП; U2 - количество команд в буфере; U3 - указывает сколько времени осталось до завершения выполнения команды в процессоре. Построим граф переходов данной системы.
Граф переходов содержит 6(n+1) состояний. Найдем ДЗ. Выписать все уравнения и определить вероятности простоя как ЦП, так и ОП.
Лекция №6. Пример.
Определим состояние системы тремя параметрами U1U2U3, где U1 - указывает сколько времени осталось до завершения считывания команды из ОП; U2 - количество команд в буфере; U3 - показывает выполняется (1) или не выполняется (0) команда в ЦП. Построим граф переходов данной системы.
Составим систему уравнений
В данной системе одно уравнение линейно зависимо, следовательно надо отбросить любое уравнение и добавить уравнение нормировки. Решается эта система любым из известных способов.
Найдем
Лекция №7. Лекция №8
Мы получили систему дифференциальных уравнений первого порядка:
Одно из этих уравнений необходимо отбросить и добавить уравнение нормировки:
 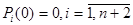
Изменить
Если наблюдать за системой достаточно долго, то можно говорить о некотором стационарном поведении системы. Решается эта система достаточно сложно. Стационарные характеристики такой системы получаются достаточно легко:
Следовательно:
Решим получившуюся систему уравнений. Из (3*) =>
Отсюда следует:
ДЗ. Пусть l=m. Чему равняется вероятность пребывания в том либо в другом состоянии? Чему равно среднее время выполнения команды этой системой. Пусть n=¥. Чему равны Рi при 1) l=m 2) l<m 3) l>m? Чему равно среднее число команд в системе при n<¥?
Вложенные цепи Маркова. Лекция №9.
Необходимо вычислить qi. Время выборки команды из ОП является случайной величиной, подчиняющейся произвольной функции распределения F(t). Пусть время выборки одной команды равно t. Разобьем это время на m одинаковых интервалов по Dt (Dt*m=t). Вероятность того, что за время Dt будет выполнена ровно одна команда в условиях экспоненциального закона распределения, равна:
Лекция №1. Введение. При разработке вычислительных машин (ВМ) и систем необходимо решить множество вопросов: «Каким должен быть объем буферной памяти (БП)? Как должна быть реализована сама БП?» и т.д. Существуют три пути решения этих вопросов. Первый путь основан на опыте разработчиков, но это означает, что мы можем получить не совсем оптимальное решение. Второй путь основан на некоторой модификации реально существующей системы. Третий путь основан на моделировании, которое бывает имитационное (используется специальный язык программирования) и аналитическое (создаются математические модели процессов, которые происходят в ВМ).
Моделирование БП типа кэш. При изучении тракта оперативная память (ОП) - БП - центральный процессор (ЦП) нужно решить: какой способ отображения использовать, размер блока, количество блоков, алгоритм замещения, дисциплина обновления ОП. В качестве критериев оптимальности могут быть использованы разные показатели. Например, время выполнения команды, программы, объем оборудования. Рассмотрим первый критерий. При выполнении команды существует несколько этапов ее выполнения, на каждом из которых тратится время. Нас интересуют этапы, связанные с обращениями к ОП. При выполнении команды может произойти не одно обращение к памяти. Рассмотрим этап, связанный с выборкой команды. Для простоты будем считать, что время выполнения команды и будет выборка ее из памяти. За командой мы сначала обращаемся к БП. Но при этом может быть «успех» или «неуспех». Введем частоту (вероятность) «неуспеха» P, тогда с вероятностью 1-Р время выборки команды равно времени обращения к БП (ТБП), а с вероятность Р время выборки команды равно сумме времен обращения к БП и ОП (ТБП+ТОП) следовательно, можно найти средне время выполнения команды: Т=(1-Р)*ТБП+Р*(ТБП+ТОП)=ТБП+Р*ТОП Определение. Обратная величина (1/Т) называется производительностью. Она показывает, сколько команд выполняется в единицу времени. ПР=1/Т=1/ ТБП+Р*ТОП
При увеличении вероятности «неуспеха» происходит резкое падение производительности. Оценим его: пусть ТБП=1; ТОП=10; Р=0.1, то ПР=1/2*ТБП - уменьшилась в два раза, следовательно, от вероятности промаха зависит производительность. Рассмотрим параметры, которые оказывают влияние на вероятность промаха. Если это влияние слабое, тогда параметр является несущественным и при моделировании его можно исключить. Если же наоборот, то этот параметр - существенный и носит название атрибут.
Структурированный подход.
При создании модели этого тракта необходимо рассмотреть две модели: модель работы БП и модель работы рабочей нагрузки. Во время выполнения программы происходит обращение за командами или за данными. В связи с этим можно говорить, что существует поток команд и данных или говорят, что существует рабочая нагрузка. Нас интересует адресная трасса - номера ячеек, к которым происходит обращение, следовательно, существует проблема задания адресной трассы при моделировании тракта ОП - БП - ЦП. Адресную трассу можно задать, используя структурированный подход. Все операторы можно разбить на следующие классы: - операторы следования; - операторы перехода; - операторы цикла. Существует доказательство, что все операторы могут быть сведены к выше перечисленным операторам. В результате получим, что адресная трасса примет вид: (i,i+1), если i-ый оператор является оператором следования; (i,i+k), если i-ый оператор - безусловный переход вперед; (i,..,i+l,i,...,i+l,...,i,...,i+l) (r раз), если i-ый оператор - оператор цикла. Получившаяся рабочая нагрузка обусловлена только наличием команд. Реальная программа состоит из комбинации этих объектов.
Лекция №2 Оценка вероятности промаха БП типа кэш. Будем выяснять вероятность «промаха» в зависимости от параметров кэш-памяти. Пусть способ отображения БП - группо-ассоциативный. Введем параметр ассоциативности S, который показывает сколько областей в БП. V-объем БП (в блоках), n-число ячеек в блоке.
1) Пусть рабочая нагрузка состоит из операторов следования. Пусть К- объем программы в блоках. Вероятность «промаха»:
При обращении к кэш-памяти за очередной командой происходит «промах» только для первой команды, принадлежащей данному блоку, т.к. в блок БП переписывается не только эта команда, но и остальные, следовательно происходит процесс опережающего ввода.
Вывод: чем больше ячеек в блоке - тем меньше вероятность «промаха». 2) Пусть программа состоит из команд следования и перехода вперед. Пусть qi - вероятность того, что после выполнения текущей команды должна выполняться команда, отстоящая от текущей на i адресов вперед. Пусть выполнилась первая команда, принадлежащая данному блоку, тогда вероятность того, что этот блок обеспечит выполнения только одной команды равна:
две команды:
ДЗ. Найти U3 и вывести рекуррентное соотношение. Найдем среднее число команд, которые дает блок:
ДЗ. Найти m, если qi=1/n (если n®¥, то можно убедится, что m=e=2,47...) Вероятность «промаха»:
Вывод: команды ветвления вперед увеличивают вероятность «промаха». 3) Программа состоит из всех трех операторов. Пусть длина цикла составляет l блоков и число повторений - r. При определении вероятности «промаха» рассмотрим три случая: 1. l £ V 2. V+V/S £ l 3. V £ l £ V+V/S Рассмотрим первый случай (l £ V).
Этот случай характерен тем, что на первом цикле (шаге) (всего r) в БП нет ни одного блока программы, следовательно, при обращении к каждому блоку программы будет, происходит один «промах». На остальных циклах промахов нет. Для простоты будем считать, что программа начинается с начала области.
Рассмотрим второй случай (V+V/S £ l) Пусть будет алгоритм замещения LRU. На первом цикле при обращении к первым V блокам программы будет происходить один «промах», а V+1 блок вытесняет первый блок БП и т.д. На втором цикле тоже происходят вытеснения. Действительно первый блок программы отсутствует в БП (вместо него V+1 блок) следовательно, произойдет вытеснение V/S+1 блока и т.д.
Рассмотрим третий случай (V £ l £ V+V/S).
На первом цикле при обращении к первым V блокам программы будет происходить один «промах», а хвост программы (l-V блоков) вытесняет первые блоки из БП. На остальных циклах вытеснения происходят только с первыми l-V блоками каждой области БП.
На рис. приведена зависимость вероятности «промаха» от длины программы, состоящей из операторов следования, ветвления и цикла. Пусть нам зафиксировали объем КЭШа и наша задача - найти параметр ассоциативности S (1£ S £.V). Если S=V, то мы имеем чисто ассоциативное отображение. Если S=1, то второй участок зависимости наиболее пологий, следовательно, мы имеем оптимальное значение параметра ассоциативности, принимая во внимание только «промах» при обращении к БП типа кэш (вероятность «промаха»).
Лекция №3
Секторное отображение.
Пусть V-объем БП, S-число секторов. Алгоритм замещения LRU.
ДЗ. Доказать, что для FIFO будет аналогично.
  Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...  Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? - задался я вопросом...  Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем...  Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|