|
|
ЧАСТЬ III. ЭЛЕКТРИЧЕСТВО и МАГНЕТИЗМСтр 1 из 6Следующая ⇒ УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК Электрический ток, сила тока и плотность тока В электродинамике – разделе учения об электричестве, в котором рассматриваются явления и процессы, обусловленные движением электрических зарядов или макроскопических заряженных тел, – важнейшим понятием является понятие электрического тока. Электрический ток есть упорядоченное движение электрических зарядов. Электрический ток, возникающий в проводящей среде вследствие того, что в нем создается электрическое поле, называется током проводимости. Электрический ток может быть обусловлен также движением в пространстве макроскопических заряженных тел (пылинок, капель жидкости) или даже одного заряженного тела. Такой ток называют конвекционным. Примером конвекционного тока может служить ток, который возникает при вращении тела, заряженного с некоторой объемной или поверхностной плотностью. К электрическому току относят и направленное движение электронов или ионов в вакууме, которое формально не подпадает под определение как тока проводимости (нет проводящей среды), так и конвекционного тока (упорядоченно перемещаются заряженные микро-, а не макрообъекты). Эти токи определяют работу электровакуумных приборов, установок ионной имплантации и ионного легирования и т. д. Для возникновения и существования электрического тока необходимо, с одной стороны, наличие свободных носителей тока – заряженных частиц, способных перемещаться упорядочено, а с другой — наличие электрического поля, энергия которого, каким-то образом восполняясь, расходовалась бы на их упорядоченное движение. За направление тока условнопринимают направление движения положительных зарядов. Количественной мерой электрического тока служит сила тока
где Физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока, называется плотностью тока:
Выразим силу и плотность тока через среднюю скорость
а плотность тока
Плотность тока – вектор,ориентированный по направлению тока, т. е. направление вектора
Понятие напряжения является обобщением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов в том случае, если на этом участке не действует эдс.
Закон Ома В 1826 г. немецкий физик Г. Ом (1787–1854) экспериментально установил закон, согласно которому, сила тока, проходящего в однородном проводнике, пропорциональна напряжению на концах проводника:
где R – характеристика проводящей среды, электрическое сопротивление проводника. В СИ сопротивление измеряется в омах (Ом). Значение сопротивления проводника R зависит от материала, из которого проводник изготовлен, а также его размеров и формы. Для однородного проводника с площадью поперечного сечения S и длиной l имеем
где Закон Джоуля–Ленца
Рассмотрим однородный проводник, к концам которого приложено напряжение U. За время
Уравнение (7.20) может быть составлено для всех замкнутых контуров, которые можно выделить мысленно в данной разветвленной цепи. Однако независимыми будут только уравнения для тех контуров, которые нельзя получить наложением других контуров один на другой. При составлении уравнений второго правила Кирхгофа токам и эдс нужно приписывать знаки в соответствии с выбранным направлением обхода. Эдс также нужно приписать знак минус, так как она действует в направлении, противоположном направлению обхода. Направления обхода в каждом из контуров можно выбирать совершенно произвольно и независимо от выбора направлений в других контурах. При этом может случиться, что один и тот же ток либо одна и та же эдс войдет в разные уравнения с различными знаками. Это, однако, не имеет никакого значения, потому что изменение направления обхода вызывает лишь изменение всех знаков в уравнении (7.20) на обратные. Число независимых уравнений, составленных в соответствии с первым и вторым правилами Кирхгофа, оказывается равным числу различных токов, текущих в разветвленной цепи. Поэтому, если заданы эдс и сопротивления для всех неразветвленных участков, то могут быть вычислены все токи.
Магнитное поле Тема 3. Магнитное поле. Закон Био-Савара-Лапласа Электрический ток создает поле, действующее на магнитную стрелку. Стрелка ориентируется по касательной к окружности, лежащей в плоскости, перпендикуляной к проводнику с током (рис. 9). Основной характеристикой магнитного поля является вектор индукция По аналогии с электрическим полем, магнитное поле также может быть изображено графически с помощью силовых линий (линий индукции магнитного поля). Силовая линия – это такая линия, касательная к которой в каждой точке совпадает по направлению с вектором индукции
Рис. 9 Для нескольких источников магнитного поля согласно принципу суперпозиции магнитных полей индукция результирующего магнитного поля равна векторной сумме индукций всех отдельных магнитных полей:
Вектор индукции Закон Био-Савара-Лапласа в векторной форме:
 , ,
где
Направление вектора В скалярном виде закон Био-Савара-Лапласа:
Магнитное поле линейного тока. Для нахождения индукции В произвольной точке М, удаленной от оси проводника на расстояние b (рис. 11), векторы
По закону Био-Савара-Лапласа модуль вектора магнитной индукции
В качестве переменной интегрирования выберем угол Из рисунка 11 следует, что Тогда
Из прямоугольного треугольника DOM:
Следовательно, индукция dB, создаваемая элементом проводника dl с током I:
Теперь можно перейти к интегрированию:
Так как угол
Следовательно,
Магнитное поле в центре кругового проводника с током. Для нахождения индукции магнитного поля в центре кругового проводника с током необходимо разбить этот проводник на элементы По закону Био-Савара-Лапласа модуль вектора
Так как все элементы Тогда выражение для модуля вектора
Теперь для нахождения модуля вектора
Следовательно, индукция магнитного поля B в центре кругового проводника радиусом R с током I:
Тема 8. Уравнения Максвелла УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
ЧАСТЬ III. ЭЛЕКТРИЧЕСТВО и МАГНЕТИЗМ ЭЛЕКТРОСТАТИКА Тема 1. Теорема Остроградского-Гаусса для электростатического поля
Многие физические явления, наблюдаемые в природе и окружающей нас жизни, не могут быть объяснены только на основе законов механики, молекулярно-кинетической теории и термодинамики. В этих явлениях проявляются силы, действующие между телами на расстоянии, причем эти силы не зависят от масс взаимодействующих тел и, следовательно, не являются гравитационными. Эти силы называют электромагнитными силами. О существовании электромагнитных сил знали еще древние греки. Но систематическое, количественное изучение физических явлений, в которых проявляется электромагнитное взаимодействие тел, началось только в конце XVIII века. Трудами многих ученых в XIX веке завершилось создание стройной науки, изучающей электрические и магнитные явления. Эта наука, которая является одним из важнейших разделов физики, получила название электродинамики. Основными объектами изучения в электродинамике являются электрические и магнитные поля, создаваемые электрическими зарядами и токами.
Электростатическое поле – это особый вид материи, с помощью которой происходит взаимодействие заряженных тел.
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда. В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:
Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному заряду e. В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером. Атом данного вещества может потерять один или несколько электронов или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион. В системе СИ элементарный заряд e равен:
Заряд может передаваться от одного тела к другому только порциями, содержащими целое число элементарных зарядов. Таким образом, электрический заряд тела – дискретная величина:
Физические величины, которые могут принимать только дискретный ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда. Следует отметить, что в современной физике элементарных частиц предполагается существование так называемых кварков – частиц с дробным зарядом Однако, в свободном состоянии кварки до сих пор наблюдать не удалось.
Точечным называется заряд, сосредоточенный на теле, размерами которого можно пренебречь по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует.
Закон Кулона:сила взаимодействия F между двумя неподвижными точечными зарядами q 1 и q 2 прямопропорциональна величинам этих зарядов и обратно пропорциональна квадрату расстояния r между ними:
где e – диэлектрическая проницаемость среды, показывающая во сколько раз сила взаимодействия зарядов в данной среде меньше, чем в вакууме. Кулоновская сила Электрические поля, которые создаются неподвижными электрическими зарядами, называются электростатическими.
Для обнаружения и опытного исследования электростатического поля можно использовать пробный точечный заряд q 0 . Если этот заряд поместить в какую- либо точкуэлектростатического поля,то на него будетдействовать сила Напряженность электростатического поля в данной точке есть физическая величина
Напряжённость электростатического поля, создаваемого точечным зарядом q в любой точке поля, находящейся на расстоянии r от этого заряда:
Силовая линия — это такая линия, касательная в каждой точке к которой совпадает по направлению с вектором напряженности электростатическго поля в данной точке (рис. 1, 2). Рис. 1 Рис. 2 Если поле создается точечным зарядом, то силовые линии – это радиальные прямые, выходящие из положительного заряда (рис. 2, а), и входящие в отрицательный заряд (рис. 2, б). С помощью силовых линий можно характеризовать не только направление, но и величину напряженности электростатического поля, связывая её с густотой силовых линий. Большей густоте силовых линий соответствует большая величина напряженности (рис. 1, 2). Количественно числу силовых линий, пронизывающих единичную площадку, расположенную перпендикулярно силовым линиям, ставится в соответствие величина напряженности электростатического поля. В этом случае определенному заряду q, создающему поле, соответствует определенное число N силовых линий, выходящих (для
Поток вектора напряженности электростатического поля Если площадка S перпендикулярна силовым линиям (рис. 3), то поток ФЕ вектора напряженности
Рис. 3 Рис. 4
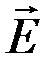 через данную площадку S: через данную площадку S:
где α – угол между векторами напряженности
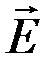 через произвольную поверхность S, необходиморазбить эту поверхность на элементарные площадки dS (рис. 5),определить элементарный поток dФЕ через каждую элементарную площадку dS по формуле: через произвольную поверхность S, необходиморазбить эту поверхность на элементарные площадки dS (рис. 5),определить элементарный поток dФЕ через каждую элементарную площадку dS по формуле:  , ,
а затем все эти элементарные потоки dФЕ сложить, что приводит к интегрированию:
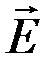 и нормали и нормали  к данной элементарной площадке dS. к данной элементарной площадке dS.
Если ввести вектор
Теорема Остроградского - Гаусса для электростатического поля. Теорема Остроградского - Гаусса для электростатического поля связывает между собой величину потока ФЕ вектора напряженности электростатического поля в вакууме через произвольную замкнутую поверхность S с величинойзаряда q, заключенного внутри данной замкнутой поверхности S (рис. 6).
 ) или входящие в заряд (для ) или входящие в заряд (для 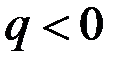 ), пронизываютпроизвольную замкнутую поверхность S, охватывающую этот заряд (рис. 6), то величина потока ФЕ вектора напряженности электростатического поля через эту произвольную замкнутую поверхность S будет определяться числом N силовых линий, выходящих из заряда (для ), пронизываютпроизвольную замкнутую поверхность S, охватывающую этот заряд (рис. 6), то величина потока ФЕ вектора напряженности электростатического поля через эту произвольную замкнутую поверхность S будет определяться числом N силовых линий, выходящих из заряда (для  ) или входящих в заряд (для ) или входящих в заряд (для 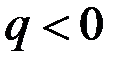 ): ):
Это соотношение есть теорема Остроградского-Гаусса дляэлектростатического поля.
Таккак поток считается положительным, если силовые линии выходят из поверхности S, и отрицательным для линий, входящих в поверхность S, то в случае, если внутри произвольной замкнутой поверхности S находится не один, а несколько (n) разноименных зарялов, то теорема Остроградского - Гаусса для электростатического поля формулируется следующим образом:
поток вектора напряженности электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e0:
В общем случае электрические заряды могут быть распределены внутри объёма, ограниченного замкнутой поверхностью S, с некоторой объемной плотностью В таком случае теорема Остроградского - Гаусса приобретает вид:
Напряженность электростатического поля зависит от диэлектрических свойств среды. В диэлектрике напряженность поля меньше, чем напряженностьвнешнего электростатического поля в вакууме, в котором находится диэлектрик, в e раз (e – диэлектрическая проницаемость среды), а модуль вектора
Вектор электрического смещения Используя то, что в вакууме
то есть поток вектора смещения В случае, если электрические заряды распределены внутри объёма V, ограни-ченного замкнутой поверхностью S, с некоторой объемной плотностью
Тема 2. Работа сил электростатического поля. Потенциал Если в электростатическом поле, создаваемом точечным зарядом q, перемещается другой пробный заряд q 0из точки 1 в точку 2 вдоль произвольной траектории (рис. 7), то при этом совершается работа сил электростатического поля.
Из рисунка 7 видно, что Тогда
то есть работа при перемещении заряда из точки 1 в точку 2 в электростатическом поле не зависит от траектории перемещения, а определяется только положениями начальной (1) и конечной (2) точек, то есть электростатическое поле точечного заряда является потенциальным.
Работа, совершаемая силами электростатического поля при перемещении заряда q 0из точки 1 в точку 2, выражается следующим образом:
где φ1 и φ2 – потенциалы электростатического поля в точках 1 и 2.
Потенциал электростатического поля определяется с точностью до произвольной аддитивной постоянной С, то есть для поля точечного заряда q:
Тогда
Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой
Если считать, что при удалении на бесконечность потенциал электростатического поля обращается в нуль (φ∞ =0), то потенциал φ1 в данной точке поля можно определить следующим образом:
то есть потенциал j в данной точке поля равен работе сил электростатического поля при перемещении точечного положительного единичного заряда из данной точки поляна бесконечность. Циркуляцией вектора напряженности
Для того, чтобы найти циркуляцию вектора напряженности Однако для электростатического поля циркуляция вектора напряженности
С одной стороны, эта работа равна:
а с учетом того, что
С другой стороны, эта работа может быть определена с помощью формулы:
из которой следует, что для произвольного замкнутого контура эта работа равна нулю, так как
 Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор...  Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот...  Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем...  Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|