| № п/п
| Вопрос
| Ответ
|
| 1.
| Процесс увеличения суммы денег в связи с начислением процентов называют …
|
|
| 2.
| В случае, когда наращенная сумма определяется по отношению к неизменной базе, имеют дело с … процентами.
|
|
| 3.
| В случае, когда исходная сумма меняется, имеют дело с … процентами.
|
|
| 4.
| При начислении простых процентов наращенная сумма определяется по формуле
| 1. P(1+ ni);
2.  ;
3. ;
3.  ;
4. Pn(1 + i);
5. P(n +i). ;
4. Pn(1 + i);
5. P(n +i).
|
| 5.
| При определении числа дней пользования ссудой применяется … подхода.
| 1. Один
2.Два
3.Три
4. Четыре
|
| 6.
| Наращенная сумма по сложным процентам определяется по формуле
| 1.P(1 + i) n
2. n(P + i);
3.  ;
4. P(1 + n) i;
5. ;
4. P(1 + n) i;
5. 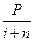
|
| 7.
| Ставки, обеспечивающие равноценность финансовых последствий, называются …
|
|
| 8.
| Множитель наращения по простым ставкам определяется по формуле
| 1. (1 + n)i;
2. (1 + i)n;
3.(1 + ni);
4. (n + i)-1;
|
| 9.
| Возможны, и применяются на практике … варианта простых процентов.
| 1. Два
2. Три
3.Четыре
|
| 10.
| Точные проценты с точным числом дней ссуды – это ….
| 1. АСТ/АСТ
2. АСТ/360
3. 360/360
|
| 11.
| Процесс удержания процентов непосредственно перед выдачей кредита называется ….
|
|
| 12.
| В зависимости от вида процентной ставки применяются … метода дисконтирования.
| 1. Два
2. Три
3. Четыре
|
| 13.
| Для ставки наращения прямой задачей является определение наращенной суммы, обратной - ….
|
|
| 14.
| Для учетной ставки прямая задача заключается в дисконтировании, обратная -
|
|
| 15.
| Ставки, при которых результаты наращения или дисконтирования будут одинаковыми, называются ….
|
|
| 16.
| … проценты применяются в финансовых операциях, если проценты не выплачиваются сразу, а присоединяются к сумме долга.
|
|
| 17.
| Наращенная сумма на коне срока по сложной ставке вычисляется по формуле …
| 1. P(1 + i) n;
2. n(P + i);
3.  ;
4. P(1 + n) i
5. ;
4. P(1 + n) i
5. 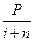
|
| 18.
| Величину … называют множителем наращения по сложной ставке.
| 1. (1 + n)i;
2. (1 + i)n;
3. (1 + ni);
4. (n + i)-1;
|
| 19.
| Величина множителя наращения зависит от … параметров.
| 1. Двух
2. Трех
3.Четырех
4.Пяти
5.Шести
|
| 20.
| Для срока меньше года простые проценты … сложных.
| 1. Меньше
2. Больше
3. Равны друг другу
|
| 21.
| Ставка, измеряющая тот реальный относительный доход, который получается за год, называется ….
|
|
| 22.
| Дисконтирование по сложной учетной ставке осуществляется по формуле …
| 1.S(1 – n)d
2. S(1 –nd)
3. (S – nd)-1
4.  5. S(1 – d)n
5. S(1 – d)n
|
| 23.
| Формулы эквивалентности ставок получают исходя из равенства ….
|
|
| 24.
| Платежи, которые, будучи «приведенными» к одному моменту времени, оказываются равными, называются ….
|
|
| 25.
| 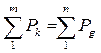 - это уравнение … финансовых платежей. - это уравнение … финансовых платежей.
|
|
| 26.
| Процесс общего роста цен, приводящий к снижению покупательной способности, называется …
|
|
| 27.
| Темп инфляции определяется по формуле ….
| 1. 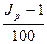 2. (1 – Jp)×100
3. (100 –Jp)-1
4. 100(Jp – 1)
5.
2. (1 – Jp)×100
3. (100 –Jp)-1
4. 100(Jp – 1)
5.  × 100 × 100
|
| 28.
| Постоянный темп инфляции 5%. Определите рост цен за год.
| 1. 60%
2. 79,6%
3. 80%
4. 76,9%
5.69,7%
|
| 29.
| Индекс цен определяется по формуле
| 1. 100 +  2. 1 +
2. 1 + 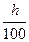 3.
3. 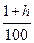 4. (100 + h)-1
5.
4. (100 + h)-1
5. 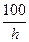 + 1 + 1
|
| 30.
| Индекс цен за несколько периодов равен … цепных индексов цен.
| 1. Сумме
2. Разности
3. Произведению
4. Отношению
|
| 31.
| Увеличение наращенной суммы с учетом ее инфляционного обесценения имеет место только при ….
| 1. 1 + ni < Jp
2. 1 + ni = Jp
3. 1 + ni > Jp
|
| 32.
| Предоставление денег или товаров в долг на условиях возвратности с уплатой процентов – это ….
| 1. Трансферт
2. Кредит
3. Дотация
|
| 33.
| Если предполагается отдать заем одним платежом, то размер этого платежа вычисляется по формуле ….
| 1. D(1 + n i)
2. D(1 + i)n
3. D(n + i)
4. D(1 + n) i
5. D(n i)-1
|
| 34.
| Срочная уплата долга является сумма двух величин …
| 1. Ставки по займу и проценты по займу
2. Проценты по займу и расходы по погашению основного долга.
3. Расходы по погашению основного долга и общего срока займа.
|
| 35.
| Если производить погашение основного долга равными ежегодными платежами, то размеры платежей равны …
| 1. D - n
2. n -D
3. 
|
| 36.
| При значительных размерах кредита, заемщик для своевременного погашения долга предусматривает ….
| 1. Создание погасительного фонда.
2. Создание плана расчета за заем.
3. Возможность увеличения срока оплаты.
|
| 37.
| Срочная уплата в погасительный фонд, при начислении простых процентов определяется как….
| 1. D + gR
2. (D + R)g
3. Dg + R *
4. (D + g)R
5. D(R +g)
|
| 38.
| Сумма взносов и начисленных процентов, накопленных в погасительном фонде должна быть равна ….
| 1. Сумме разового долга
2. Величине погасительного платежа.
3.Сумме долга на момент его погашения.
|
| 39.
| Плата, выраженная в процентах от суммы долга, которую взимают банки с заемщика за пользование кредитными деньгами называется ….
|
|
| 40.
| Финансовые средства, вкладываемые в объекты предпринимательской деятельности с целью получения прибыли – это ….
|
|
| 41.
| Методы без дисконтирования распределенных во времени сумм называют ….
| 1. Бухгалтерскими
2. Дисконтными
3. Динамическими
|
| 42.
| Методы, учитывающие фактор времени называют ….
| 1. Бухгалтерскими
2. Дисконтными
3. Статическими
|
| 43.
| Разность между дисконтируемыми показателями чистого дохода и инвестиционных затрат называется ….
| 1. Чистым приведенным доходом.
2. Внутренней нормой доходности.
3. Суммой процентов
|
| 44.
| Ставка «уравновешивающая» инвестиции и доходы, распределенные во времени называется ….
| 1. Чистым приведенным доходом.
2. Внутренней нормой доходности.
3. Суммой процентов
|
| 45.
| Чем больше сумма капитальных вложений, тем … чистый приведенный доход (при одинаковых поступлениях)
| 1. больше
2. меньше
|
| 46.
| С ростом ставки приведения, размер чистого приведенного дохода ….
| 1. возрастает
2. сокращается
3. не изменяется
|
| 47.
| По мере увеличения продолжительности периода поступлений дохода величина чистого приведенного дохода ….
| 1. увеличивается
2. уменьшается
3. не изменяется
|
| 48.
| Дисконтирование членов потока производится по ставке внутренней нормы доходности, тогда чистый приведенный доход равен ….
| 1. 50
2. 100
3. 1
4. 0
5. 25%
|
| 49.
| Расчетное время, необходимое для полной компенсации инвестиций называется …. окупаемости
|
|
| 50.
| В простом случае срок окупаемости определяется как … инвестиций и средней величины доходов.
| 1. Сумма
2. Разность
3. Произведение
4. Отношение
|
| 51.
| Отсрочка поступлений доходов … срок окупаемости.
| 1. Увеличивает
2. Уменьшает
3. Не изменяет
|
| 52.
| Срок окупаемости растет с … ставки приведения.
| 1. Увеличением
2. Уменьшением
|
| 53.
| Рентабельность и срок окупаемости находятся в … зависимости.
| 1. В прямой
2. В обратной
|
| 54.
| Отношение суммы дисконтированных доходов к величине дисконтированных инвестиций называется … доходности
| Индексом
|
| 55.
|
Проект рентабелен, если индекс доходности ….
| 1. Больше 0
2. Больше 1
3. Меньше 1
|
| 56.
| … - это стратегия уменьшения риска посредством распределения инвестиций между несколькими направлениями деятельности.
| Диверсификация.
|
| 57.
| Что такое чистая текущая стоимость проекта:
| а) суммарная чистая прибыль от реализации проекта;
б) разность между суммарным дисконтированным денежным потоком и дисконтированными инвестициями.
|
| 58.
| Как обычно влияет финансирование проекта за счет эмиссии акций на рентабельность собственного капитала (отдачу на собственный капитал):
| а) увеличивается;
б) снижается;
в) не изменяется.
|
| 59.
| Что такое внутренняя ставка доходности проекта:
| а) доходность инвестиционных вложений в данный проект;
б) ставка дисконтирования, при которой достигается только окупаемость инвестиционных вложений.
|
| 60.
| Петров всем видам вложений предпочитает краткосрочные облигации: покупает, хранит их до срока погашения, а затем реинвестирует поступившие средства. В официальных источниках годовая доходность подобных облигаций рассчитывается по правилу простой ставки. На данный момент у Петрова имеются две возможности: трехмесячные облигации с доходностью 24% или шестимесячные, у которых доходность равна
24,5%. Какие облигации выгоднее:
| 1) трехмесячные;
2) шестимесячные;
3) никакой разницы, доход за год будет одинаков.
|
| 61.
| Фирма желает взять заем на покупку нового оборудования, которое будет стоить 20000 ден. ед. и служить 1 год. Ожидается, что благодаря этому дополнительный годовой доход составит 1500 ден. ед. Фирма осуществит инвестиции в оборудование при условии, что процентная ставка составит:
| 1)6%;
2) 8%;
3) 10%;
4)15%;
5) 4%.
|
| 62.
| Если темп инфляции увеличивается, то при прочих равных условиях в соответствии с эффектом Фишера (правилом компенсации)
| 1) номинальная и реальная ставки процента понизятся;
2) номинальная и реальная ставки процента повысятся;
3) номинальная и реальная ставки процента не изменятся;
4) номинальная ставка процента повысится, реальная — не изменится
|
| 63.
| Индивидуальный предприниматель купил оборудование на сумму 250 тыс. руб., рассчитывая продать его в конце 1-го года за 300 тыс. руб. за вычетом налогов. Предполагаемая доходность инвестиций составит:
| 1) 10%;
2) 15%;
3) 20%;
4) 25%.
|
| 64.
| Если номинальная процентная ставка составляет 10%, а
темп инфляции определен в 4% в год, то реальная процентная ставка составит:
| 1) 14%;
2) 6%;
3) 2,5%;
4) 6%;
5) 4%.
|
| 65.
| В год «1» уровень цен не изменяется, номинальная ставка процента составляет 6%. В год «2» темп инфляции составил 3%. Если реальная ставка процента в году «2» на том же уровне, что и в году «1», то номинальная ставка процента в году «2» должна:
| 1) вырасти на 9%;
2) вырасти на 3%;
3) снизиться на 3%;
4) вырасти на 6%;
5)остаться неизменной на уровне 6%.изменится;
5) номинальная ставка процента не изменится, реальная
снизится.
|
| 66.
| По условиям одного из двух обязательств должно быть выплачено 500 тыс. руб. через 4 месяца; второго —540 тыс. руб. через 8 месяцев. Применяется простая процентная ставка 18%. Какое из этих условий выгоднее для должника:
| 1) первое;
2) второе;
3) равноценны.
|
| 67.
| Проценты на проценты начисляются в схеме:
| 1) сложных процентов;
2) простых процентов;
3) как сложных, так и простых процентов;
|
| 68.
| Если реальная ставка инвестирования в году была равна 6,0%, а номинальная — 11,3%, то каков был уровень
инфляции в этом году?
| 1)5,3%;
2) 5%;
3) 105%
|
| 69.
| Капитал в 1 млн. руб. может быть помещен в банк на 3 месяца с ежемесячным начислением 3% (по ставке сложных процентов) или на срочный вклад на 3 месяца, по которому в конце 3-го месяца начисляется 9%. Определить наиболее предпочтительный способ помещения капитала:
| 1) второй;
2) первый;
3) никакой разницы, доход одинаковый.
|
| 70.
| Вкладчик рассматривает три доступных ему способа вложения денег на ближайшее полугодие:
а) в банк на 6 месяцев с ежемесячным начислением процентов исходя из годовой ставки 12%;
б) с трехмесячным начислением под 12,4% годовых;
в) срочный валютный депозит (в долл. США) на 6 месяцев при 8,5% в год. Текущий курс составляет 28 руб. и согласно прогнозам поднимется до 28,5 руб. за 1 долл. к концу полугодия. Расположить эти способы в порядке убывания выгодности:
| 1) а, б, в;
2) в, б, а;
3) б, в, а;
4) б, а, в.
|
| 71.
| Рассматриваются следующие схемы обслуживания долгосрочной задолженности:
а) равными срочными уплатами;
б) разовое погашение в конце срока;
в) равными процентными выплатами.
Расположить в порядке убывания остатка задолженности на любую промежуточную дату:
| 1) б, в, а;
2) а, б, в;
3) а, в, б;
4) в, а, б.
|
| 72.
| У заемщика имеется 2 возможных варианта заимствования необходимой ему суммы под 8% годовых на 180 дней с момента подписания договора:
По всем рассматриваемым вариантам принята одна и та же временная база, равная 360 дням. Какой вариант вы бы ему рекомендовали?
| 1) по простой ставке начисления процентов;
2) по сложным процентам с ежемесячной капитализацией процентов;
|
| 73.
| При выдаче ссуды на 180 дней под 10% годовых по простой ставке кредитором удержаны комиссионные в размере 0,5% суммы кредита. Какова эффективность ссудной операции в виде годовой ставки сложных процентов при условии, что год равен 360 дням:
| 1) 11,05%;
2) 11,36%;
3) 10,25%;
|
| 74.
| При выдаче кредита в 6000 руб. на 60 дней под 30% годовых по простой ставке кредитором в момент его предоставления были удержаны проценты. Какова доходность кредитной операции, измеряемая простыми процентами?
| 1) 32,46%;
2) 30,95%;
3) 31,58%.
|
| 75.
| Долг, равный 300 тыс. руб., необходимо погасить за 3 года. За заем выплачиваются проценты по ставке 10% годовых. Расположить в порядке возрастания среднего срока срочной уплаты следующие схемы погашения:
а) равными частями долга;
б) разовое погашение в конце срока;
в) равными процентными выплатами;
| 1) а, б, в;
2) а, в, б;
3) в, а, б;
4) в, б, а.
|
| 76.
| Субъект направляет свои деньги на приобретение государственных ценных бумаг лишь в случае, если:
| 1) процентные ставки скоро вырастут;
2) процентные ставки значительно сократятся;
3) процентные ставки сначала вырастут, а затем снизятся;
4) будет наблюдаться инфляционный рост цен;
|
| 77.
| Цена на колл-опцион становится тем меньше, чем при прочих равных:
| 1) выше цена базисной акции;
2) выше цена исполнения;
3) выше безрисковая ставка процента;
4) больше времени до даты истечения;
5) ниже риск базисной акции.
|
| 78.
| Рента пренумерандо это:
|
1)рента, образуемая платежами после некоторого указанного момента времени;
2) рента, платежи которой поступают в начале каждого периода;
3) рента, платежи которой скорректированы на величину налога;
4) рента, платежи которой скорректированы с учётом инфляции.
|
| 79.
| Какая должна быть номинальная ставка при ежемесячном начислении процентов, чтобы обеспечить эффективную ставку 20%?
| 1) 16,8%;
2) 13,8%;
3) 18,37%;
4) 12,2%.
|
| 80.
| Финансовая рента это:
| 1) поток платежей, все члены которого положительные величины, а временные интервалы постоянны;
2) величина каждого отдельного платежа ренты;
3) ставка, применяемая для расчёта процентов при учёте векселей;
4) рента с изменяющимися членами.
|
| 81.
| Что такое период ренты?
| 1) временной интервал между двумя соседними платежами;
2) временной интервал от начала ренты до конца ее последнего периода;
3) время первого платежа;
4) время последнего платежа.
|
| 82.
| Множитель наращения это:
| 1) отношение наращенной суммы ренты к сумме её годовых платежей или к размеру отдельного платежа;
2) множитель, который показывает во сколько раз наращенная сумма больше первоначальной;
3) отношение современной стоимости ренты к сумме её годовых платежей или к размеру отдельного платежа;
4) рента с изменяющимися членами.
|
| 83.
| Наращенная сумма ссуды это:
| 1) процесс увеличения денег в связи с присоединением процентов к сумме долга;
2) множитель, который показывает, во сколько раз увеличилась первоначальная сумма вклада;
3) ставка процента, скорректированная на инфляцию;
4) первоначальная её сумма вместе с начисленными на неё процентами к концу срока.
|
| 84.
| В каком случае обычно используется простая процентная ставка:
| 1) при долгосрочном кредитовании;
2) при краткосрочном кредитовании;
3) при ипотеке.
|
| 85.
| Что не учитывает срок окупаемости проекта:
| а) объем инвестиций;
б) требуемую инвесторами доходность;
в) денежные потоки за пределами срока окупаемости.
|
| 86.
| При каком виде лизинга не предусматривается переход предмет лизинга в собственность лизингополучателя:
| а) финансовом;
б) возвратном;
в) оперативном.
|
| 87.
| Фактор времени в финансовых вычислениях учитывается:
| а) с помощью множителя затрат;
б) с помощью начисления процентов;
в) начальной суммой ссуды.
|
| 88.
| Процентами в финансовых расчетах называют:
| а) наращенную сумму долга;
б) процентную ставку;
в) абсолютную величину дохода от предоставления денег в долг.
|
| 89.
|
Субъект, предоставляющий деньги в долг есть:
| а) кредитор;
б) заемщик;
в) налогоплательщик
|
| 90.
| Процентная ставка представляет собой:
| а) коэффициент наращения;
б) инструмент наращения долга;
в) величину ссуды с последующей выплатой процентов;
г) отношение суммы процентных денег, выплачиваемых за определенный отрезок времени к величине ссуды.
|
| 91.
| Наиболее часто проценты начисляются:
| а) выборочно;
б) дискретно;
в) непрерывно.
|
| 92.
| Наращением или ростом первоначальной суммы называют:
| а) рост процентной ставки за последующие периоды начисления процентов;
б) увеличение денег в связи с присоединением процентов к сумме долга;
в) различные виды процентных ставок.
|
| 93.
| В количественном финансовом анализе процентная ставка является:
| а) показателем степени доходности финансовой операции;
б) инструментом способа начисления процентов;
в) коэффициентом, определяющим степень конечной суммы долга.
|
| 94.
| Простыми процентами называются проценты:
| а) начисляемые периодически в течение всего срока ссуды;
б) часть начальной суммы долга;
в) начисляемые на одну и ту же начальную сумму.
|
| 95.
| Сложными процентами называются проценты, которые начисляются:
| а) один раз в год;
б) ежеквартально;
в) на сумму с начисленными на нее процентами в предыдущем периоде;
г) в течение всего срока ссуды.
|
| 96.
| Наращенная сумма ссуды есть:
| а) первоначальная ее сумма вместе с начисленными на нее процентами;
б) сумма долга, выплаченная раньше обозначенного срока;
в) изменение суммы долга по сложным процентам.
|
| 97.
| Формула наращения по простым процентам:
| а) P(1-n/i);
б)P(1+n/i);
в) P(i+ni);
г) P/(1+ni).
|
| 98.
| Наращенная сумма всегда:
| а) больше первоначальной суммы;
б) меньше первоначальной суммы;
в) равна первоначальной сумме.
|
| 99.
| При первоначальной сумме ссуды 10000 руб. и процентной ставке простых процентов 12 % годовых наращенная сумма через два года составит:
| а) 13000 руб.;
б) 12600 руб.;
в) 12400 руб.
|
| 100.
| Коэффициент наращения при процентной ставке простых процентов 10% годовых за три года составит:
| а) 1,25
б) 2,15
в) 1,5
г) 1,3
|
| 101.
|
Обыкновенный (коммерческий) процент получают, когда за базу сравнения берут:
|
а) действительное число дней в году (К = 365)
б) число дней в году (К=360)
с) непрерывное начисление процентов.
|
| 102.
| Наращенная сумма за 100 дней при процентной ставке простых процентов 7% первоначальной сумме 50000 руб. и при точном проценте составит:
| а) 50959 руб.
б) 51125 руб.
в) 50324 руб.
|
| 103.
| Формула наращенной суммы при простых переменных процентных ставках:
| а) S(1 - ∑ nkik);
б) Р(1+кn);
в) Р(1 + ∑ nkik).
|
| 104.
| Множитель наращения за 1 год при ставках простых процентов за 1-ое полугодие – 12% годовых и за 2-ое полугодие – 10% годовых составит:
| а) 1,25;
б) 1,11;
в) 1,17.
|
| 105.
| Реинвестирование есть процесс, когда:
| а) сумма долга погашается частями;
б) сумма депозита возвращается в установленный срок;
в) сумма с процентами опять инвестируется.
|
| 106.
| При трехкратном реинвестировании через каждый год первоначальная сумма в 15000 руб. за 3 года при простой процентной ставке 8% годовых возрастает до величины:
| а) 17398 руб.;
б) 20157 руб.;
в) 18896 руб.
|
| 107.
| Дисконтирование есть:
| а) определение суммы долга на любой последующий момент времени;
б) операция наращения начальной суммы долга;
в) задача, обратная наращению процентов.
|
| 108.
| Величину начальной суммы долга, найденную дисконтированием, называют:
| а) приведением;
б) коммерческим учетом;
в) современной величиной конечной суммы долга.
|
| 109.
| При математическом дисконтировании для определения текущей стоимости используется соотношение:
| а) а) Р= S(1+ni);
б) Р= S /(1+ni);
в) Р= S + кn.
|
| 110.
| Для расчета процентов при коммерческом учете используется:
| а) ставка наращения;
б) учетная ставка;
г) переменная ставка процентов.
|
| 111.
| Для указанной в векселе суммы 20000 руб. при сроке ссуды 1,5 года и учетной ставке 7% годовых фактически полученная заемщиком сумма составляет:
| а) 18200 руб.;
б) 17100 руб.;
в) 17900 руб.
|
| 112.
| Заемщику выплачена сумма 10200 руб. при указанной сумме долга в векселе 15000 руб. Ссуда выдана сроком на 2 года. Такие условия соответствуют учетной ставке:
| а) 16%
б) 12%
в) 9%.
|
| 113.
| Ссуда выдана на 120 дней по простой учетной ставке 7% годовых. Заемщик получил 18100 руб. Какая сумма долга проставлена в векселе при таких условиях. Временная база составляет 360 дней.
| а) 19627 руб.
б) 18532 руб.
в) 18800 руб.
|
| 114.
| Платежное обязательство составлено на 100 дней, где указана сумма ссуды 1 млн. рублей. Сумма выдана под учетную ставку простых процентов 12 % годовых. Сумма полученная заемщиком составляет (при К = 360 дней):
| а) 1010125 руб.;
б) 925102 руб.;
в) 966667 руб.
|
| 115.
| При простой ставке наращения 10 %, начальной сумме долга 12000 руб., конечной сумме долга 15000 руб. продолжительность ссуды (в годах) составляет:
| а) 1,5 года;
б) 2,0 года;
в) 2,75 года;
г) 2,5 года.
|
| 116.
| Уровень процентов ставки может служить:
| а) критерием эффективности финансовой операции;
б) альтернативой выбранной схемы расчета;
в) процентными деньгами.
|
| 117.
| Уровень простой процентной ставки можно определить по формуле:
| а) 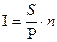 ;
б) I=(S-P)∙P∙H;
в) I=(S-P)/P∙n. ;
б) I=(S-P)∙P∙H;
в) I=(S-P)/P∙n.
|
| 118.
| Наращение по простым процентам для кредитора выгодно при продолжительности срока ссуды n:
| а) 2 года;
б) 4 года;
в) меньше одного года.
|
| 119.
| Присоединение начисленных процентов к сумме, которая являлась базой для их начисления, называют:
| а) дисконтированием;
б) наращивание по сложным процентам;
в) капитализацией процентов.
|
| 120.
| Формула наращения по сложным процентам:
| а) S=P(1-in);
б) S=P(1+in);
в) S=P/(1-in);
г) S=P(1+i)n
|
| 121.
| Срок ссуды составляет три года. Первоначальная сумма равна 10000 руб. Сложная процентная ставка наращения составляет 12 % за первый год, 10 % - за 2-й и 3-й год. Наращенная сумма через 3 года составит:
| а) 13552 руб.;
б) 14227 руб.;
в) 12936 руб.
|
| 122.
| Через сколько лет удвоится сумма при ставке простых процентов 6 % годовых:
| а) 6,5 года;
б) 16,7 года;
в) 12,3 года.
|
| 123.
| Сколько лет необходимо ждать (приближенно) пока сумма удвоится по ставке сложных процентов 6% годовых:
| а) 7,3 года;
б) 13,52 года;
в) 11,67 года.
|
124.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|
©2015- 2026 zdamsam.ru Размещенные материалы защищены законодательством РФ.