|
Погрешности прямых измерений
 Теория случайных погрешностей основана на законах теории вероятностей и математической статистике. Дадим несколько определений. Случайным событием называется такое событие, появление которого в данных условиях невозможно точно предсказать. Вероятностью данного события называется отношение числа благоприятных для события случаев к числу всех возможных случаев. Событие, вероятность которого равна единице, называется достоверным. Вероятность невозможного события равна 0. Теория случайных погрешностей основана на законах теории вероятностей и математической статистике. Дадим несколько определений. Случайным событием называется такое событие, появление которого в данных условиях невозможно точно предсказать. Вероятностью данного события называется отношение числа благоприятных для события случаев к числу всех возможных случаев. Событие, вероятность которого равна единице, называется достоверным. Вероятность невозможного события равна 0.
Постулаты теории случайных погрешностей (постулаты Гаусса): 1. погрешности измерений являются непрерывным рядом значений, среднее значение является наиболее вероятным; 2. погрешности могут быть положительные и отрицательные, т.е. отклонения от среднего значения в одну и другую сторону равновероятны; 3. большие погрешности, т.е. оклонения от среднего маловероятны. Случайные ошибки не зависят от природы величины, т.е. от того какая величина измеряется (длина или сила тока).
Эти постулаты лежат в основе нормального закона распределения погрешностей, описываемого функцией Гаусса (см. Рис.). Пусть получены n измерений одной и той же величины одним и тем же прибором. Некоторое значение  этой величины является наиболее вероятным. Все остальные значения данной серии измерений распределены относительно этой величины является наиболее вероятным. Все остальные значения данной серии измерений распределены относительно 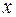 по нормальному закону. На Рис. по нормальному закону. На Рис.  - числовые значения измерений данной серии; - числовые значения измерений данной серии;  - некоторая функция, выбранная таким образом, что площадь под всей кривой распределения равна вероятности того, что истинное значение измеряемой величины находится в области всех значений - некоторая функция, выбранная таким образом, что площадь под всей кривой распределения равна вероятности того, что истинное значение измеряемой величины находится в области всех значений  , ограниченных этой кривой. Т.е. эта вероятность равна 1. , ограниченных этой кривой. Т.е. эта вероятность равна 1.
Если выделить часть этой области, ограничив ее по оси абсцисс числовым интервалом 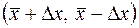 , то площадь между кривой распределения и этой частью, оси абсцисс (выделена на Рис.) будет равна вероятности , то площадь между кривой распределения и этой частью, оси абсцисс (выделена на Рис.) будет равна вероятности  того, что истинное значение того, что истинное значение 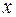 попадает в этот интервал. Числовой интервал попадает в этот интервал. Числовой интервал  называется доверительным интервалом. Величина называется доверительным интервалом. Величина  , представляющая собой вероятность того, что истинное значение измеряемой величины находится в доверительном интервале, называется доверительной вероятностью или коэффициентом надежности. , представляющая собой вероятность того, что истинное значение измеряемой величины находится в доверительном интервале, называется доверительной вероятностью или коэффициентом надежности.
В реальных условиях для конечного числа измерений пользуются не нормальным законом распределения, а распределением Стьюдента, которое при увеличении числа измерений приближается к нормальному распределению. Переход от нормального распределения к распределению Стьюдента осуществляется с помощью коэффициентов Стьюдента  , зависящих от коэффициента надежности , зависящих от коэффициента надежности  и числа измерений и числа измерений  (см. Табл.). (см. Табл.).
Таблица коэффициентов Стьюдента

| 
| | 0,1
| 0,3
| 0,5
| 0,7
| 0,8
| 0,9
| 0,95
| 0,98
| 0,99
| 0,999
| |
| 0,16
| 0,5
| 1,00
| 2.0
| 3,1
| 6.3
| 12,7
| 31,8
| 63,7
| 636,6
| |
| 0,14
| 0,45
| 0,82
| 1,3
| 1,9
| 2,9
| 4,3
| 7,0
| 9,9
| 31,6
| |
| 0,14
| 0,42
| 0,77
| 1,3
| 1,6
| 2,4
| 3,2
| 4,5
| 5,8
| 12,9
| |
| 0,13
| 0,41
| 0,74
| 1,2
| 1,5
| 2,1
| 2,8
| 3,7
| 4,6
| 8,6
| |
| 0,13
| 0,41
| 0,73
| 1,2
| 1,5
| 2,0
| 2,6
| 3,4
| 4,0
| 6,9
| |
| 0,13
| 0,40
| 0,72
| 1,1
| 1,4
| 1,9
| 2,4
| 3,1
| 3,7
| 6,0
| |
| 0,13
| 0,40
| 0,71
| 1,1
| 1,4
| 1,9
| 2,4
| 3,0
| 3,5
| 5,4
| |
| 0,13
| 0,40
| 0,71
| 1,1
| 1,4
| 1,9
| 2,3
| 2,9
| 3,4
| 5,0
| |
| 0,13
| 0,40
| 0,70
| 1,1
| 1,4
| 1,8
| 2,3
| 2,8
| 3,3
| 4,8
|
Тогда абсолютная погрешность серии из  измерений равна измерений равна  .Величина среднеквадратичной погрешности .Величина среднеквадратичной погрешности  вычисляется по формуле: вычисляется по формуле:  , где , где  - число измерений; - число измерений;  - абсолютные погрешности отдельных измерений, равные разности между отдельными и наиболее вероятным значением измеряемой величины - абсолютные погрешности отдельных измерений, равные разности между отдельными и наиболее вероятным значением измеряемой величины  . За наиболее вероятное значение . За наиболее вероятное значение  физической величины принимается среднее арифметическое значение из физической величины принимается среднее арифметическое значение из  измерений: измерений: 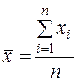 . При обработке измерений вычисляют и относительную погрешность . При обработке измерений вычисляют и относительную погрешность  . .
Схема обработки прямых измерений
- Находим среднее арифметическое
 из всех полученных значений из всех полученных значений  измеряемой величины: измеряемой величины:  . . - Определяем абсолютные погрешности
 отдельных измерений: отдельных измерений:  . . - Вычисляем
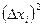 . Находим сумму . Находим сумму  . .   - Определяем среднюю квадратичную погрешность среднего арифметического:
 . . - По заданному преподавателем коэффициенту надежности
 и числу измерений и числу измерений  определяем по таблице коэффициент Стьюдента определяем по таблице коэффициент Стьюдента  . . - Находим величину абсолютной погрешности:
 . . - Вычисляем относительную погрешность:
 . . - Записываем окончательный результат в виде:

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




