Б) единичного круга на единичный круг.
a) Imz>0 на |w|<1 имеет вид W=(z-z0/z- 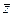 0)ei 0)ei 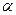 (1) (1)
где 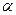 - действительно число. □Пусть дробно-линейная функция w=w(z) - действительно число. □Пусть дробно-линейная функция w=w(z)
Отображает полуплоскость на круг так, что w(z0)=0 (Imz0>0) Тогда в силу сохранения симметрии w(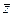 0)= 0)= 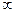 и w=A(z-z0/z- и w=A(z-z0/z- 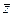 0), (так как всякое дробно линейное отобр, переводящее точку z1 в 0 а z2 в 0), (так как всякое дробно линейное отобр, переводящее точку z1 в 0 а z2 в 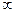 равно w=A(z-z1/z-z2)) равно w=A(z-z1/z-z2))
покажем что |A|=1. Так как точки действительной оси переходят в точки единичной окружности, то есть |w|<1 при действительных z=x то
1=|A(z-z0/z- 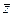 0)|= |A| (так как z-z0=z- 0)|= |A| (так как z-z0=z- 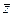 0) Следовательно A=ei 0) Следовательно A=ei 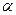 ■ Всякое комфорное отображение имеет именно вид (1) – так как по теореме Римана существует единственное такое отображение, удовлетворяющее условиям.б) |z|<1 на круг |w|<1 имеет видw=(z-z0/1-z ■ Всякое комфорное отображение имеет именно вид (1) – так как по теореме Римана существует единственное такое отображение, удовлетворяющее условиям.б) |z|<1 на круг |w|<1 имеет видw=(z-z0/1-z 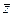 0)ei 0)ei 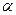 (1) (1)
где 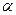 - действительно число. □Пусть дробно-линейная функция w=w(z) отображает круг |z|<1 на круг |w|<1 так, что w(z0)=0 Тогда в силу сохранения симметрии w(1/ - действительно число. □Пусть дробно-линейная функция w=w(z) отображает круг |z|<1 на круг |w|<1 так, что w(z0)=0 Тогда в силу сохранения симметрии w(1/ 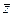 0)= 0)= 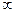 и имеем w=A(z-z0/1-z и имеем w=A(z-z0/1-z 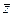 0) (так как всякое дробно линейное отобр, переводящее точку z1 в 0 а z2 в 0) (так как всякое дробно линейное отобр, переводящее точку z1 в 0 а z2 в 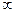 равно w=A(z-z1/z-z2)). Покажем что |A|=1. Так как точки единичной окр переходят в точки ед окр, то 1=|A(ei равно w=A(z-z1/z-z2)). Покажем что |A|=1. Так как точки единичной окр переходят в точки ед окр, то 1=|A(ei 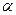 -z0/1-ei -z0/1-ei 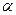 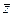 0)|=|A| (так как | ei 0)|=|A| (так как | ei 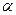 -z0|=|e-i -z0|=|e-i 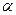 - - 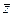 0|)Следовательно A=ei 0|)Следовательно A=ei 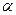 ■ ■
29. Конформные отображения элементарными функциями (z2,zn, √z, n√ z).
a) w=z2 = R2ei2 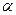 . Однолистная в области, когда в области нет точек связанных равенством z1=-z2 (нет ни одно пары точек, симметричных относительно z=0) . Однолистная в области, когда в области нет точек связанных равенством z1=-z2 (нет ни одно пары точек, симметричных относительно z=0)
Образы лучей argz= 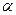 и дуг окружностей |z|= и дуг окружностей |z|= 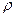 . Линии argz=const и |z|=const образуют координатную сетку на плоскости z. (полярные координаты) . Линии argz=const и |z|=const образуют координатную сетку на плоскости z. (полярные координаты)
Образы прямых Rez=с и Imz=с Взаимо однозначно переводит Rez=с в параболу v2=2p(p/2-u) а прямую Imz=с в параболу v2=2p(u+p/2) здесь p=2c2; w=u+iv;
б) w= 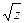 Обратная к функции w=z2: аналитическая плоскости z с выколотыми z=0, Обратная к функции w=z2: аналитическая плоскости z с выколотыми z=0, 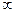 , ,
а в плоскости с разрезом, соединяющим 0 и 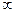 , распадается на две регулярные ветви. , распадается на две регулярные ветви.
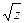 = =  ei( ei( 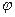 +2 +2 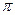 k)/2 k)/2
в) w= 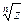 =| =| 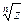 | ei( | ei( 
30. Конформные отображения функциями еz, Lnz, функцией Жуковского.
W=1/2(z+1/z) - функция регулярна в точках кроме 0 и 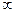 причем причем  (z)=1/2(1-1/z2) а в точках z=0 и z= (z)=1/2(1-1/z2) а в точках z=0 и z= 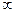 полюсы первого порядка. Однолистна в след областях полюсы первого порядка. Однолистна в след областях
1-|z|>1
2-|z|<1
3-ImZ>0
4-ImZ<0
W=ez =ex+di=|ex|edi w=eceiy c=0 – единичная окружность c<0 – единичный круг, c>0 – внешнось
W=LnZ=ln|z|+iargz+2 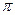 ki; ki;
Интегральная теорема Коши для односвязной области.
Пусть f – функция аналитическая в некоторой области D и её производная непрерывна, тогда для любого замкнутого контура 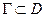


 0 0
Аналитичность интеграла с переменным верхним пределом.
Если  определена и непрерывна в D и определена и непрерывна в D и  , то , то  -- аналитична в D и -- аналитична в D и 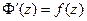 в D в D


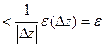
f(z) – непрерывная =>


Интегральная теорема Коши для многосвязной области.
Аналитическая функция  в в  и f(z) непрерывная => и f(z) непрерывная => 
Из данной области делаем односвязную с помощью разрезов, тогда  , но , но 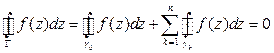
Интегральная формула Коши.
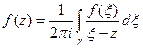 Функция Функция  дифференцируема по дифференцируема по  в области D с выколотой точкой z. Выберем в области D с выколотой точкой z. Выберем 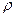 так, чтобы круг так, чтобы круг  вместе с его границей вместе с его границей  лежал внутри лежал внутри 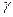 . Тогда . Тогда

где  , так как , так как  , то , то

 в силу непрерывности f(z) в силу непрерывности f(z)
Теорема о бесконечной дифференцируемости интеграла типа Коши.
Интеграл Коши  есть аналитическая функция в любой области не содержащей точек есть аналитическая функция в любой области не содержащей точек  и имеет производную любого порядка и имеет производную любого порядка 
(по индукции)

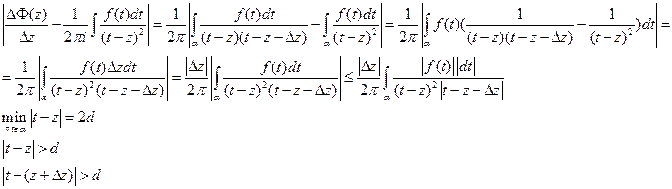 Поскольку f(t) непрерывная на замкнутом множестве, то она на нём ограничена Поскольку f(t) непрерывная на замкнутом множестве, то она на нём ограничена 
Т.о. доказали 
36.Теорема о 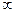 -ой дифференцируемости аналитической функции. -ой дифференцируемости аналитической функции.
Пусть  аналитична в обл-ти аналитична в обл-ти  и непрер. в замкн. обл-ти и непрер. в замкн. обл-ти  .Тогда во внутренних точках обл-ти .Тогда во внутренних точках обл-ти  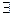 производная производная 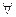 порядка ф-ии порядка ф-ии  , причём , причём  □Для доказательства достаточно повторить следующие суждения соответствующее число раз. С помощью интеграла Коши □Для доказательства достаточно повторить следующие суждения соответствующее число раз. С помощью интеграла Коши 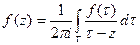 (*). Рассм. в обл-ти (*). Рассм. в обл-ти  некую замкнутую подобласть некую замкнутую подобласть  , расстояние всех , расстояние всех  которой от границы которой от границы 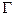 обл-ти обл-ти  некого «+» числа некого «+» числа 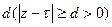 . .  - явл.аналитич-ой ф-ей - явл.аналитич-ой ф-ей  в в  , причём , причём 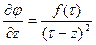 -непрерыв.ф-ия своих аргументов. В силу общих св-в интегралов, зав.от параметра, в внут. -непрерыв.ф-ия своих аргументов. В силу общих св-в интегралов, зав.от параметра, в внут.  -ах обл-ти -ах обл-ти   (**). (**) явл. интегралом, завис.от пар-ра,и его подынт. ф-ия имеет те же св-ва, что подынт.ф-ия у (*). (**). (**) явл. интегралом, завис.от пар-ра,и его подынт. ф-ия имеет те же св-ва, что подынт.ф-ия у (*).  явл.аналитич-ой ф-ей явл.аналитич-ой ф-ей  в в  ,причём для её производной верно: ,причём для её производной верно:  .■ .■
Теорема Морера.
Пусть  -непрерывная в односв.области -непрерывная в односв.области  и и 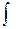 от от  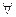 замкнутому контуру, целиком замкнутому контуру, целиком  ,равен 0. Тогда ,равен 0. Тогда  -аналитическая в обл-ти -аналитическая в обл-ти  . □При условиях теоремы . □При условиях теоремы  ,где ,где  -проихвольные -проихвольные  области области  , а , а 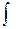 берётся по берётся по 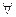 пути, соединяющему эти пути, соединяющему эти  в обл-ти в обл-ти  ,является аналитической в этой обл-ти ф-ей, причём ,является аналитической в этой обл-ти ф-ей, причём  . Но, как было только что установлено, производная аналитической ф-ии также является анал.ф-ей, т.е. . Но, как было только что установлено, производная аналитической ф-ии также является анал.ф-ей, т.е. 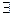 нерерывная производная ф-ии нерерывная производная ф-ии 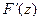 , а именно ф-ия , а именно ф-ия  ,что и доказывает теорему.■Эта теорема в определённом смысле явл. обратной по отношении к т.Коши. Её легко обобщить на многосвязные области. ,что и доказывает теорему.■Эта теорема в определённом смысле явл. обратной по отношении к т.Коши. Её легко обобщить на многосвязные области.
Принцип максимума модуля.
Пусть  -анал-ая в обл. -анал-ая в обл.  и непрерыв. в замкн. обл. и непрерыв. в замкн. обл.  .Тогда или .Тогда или  или максимальные знач-я или максимальные знач-я  достигаются только на границе области. □ достигаются только на границе области. □  по условию непрерывная в замкн.области.Она достигает своего макс.значения по условию непрерывная в замкн.области.Она достигает своего макс.значения  в какой-то в какой-то  данной обл-ти.Т.е. данной обл-ти.Т.е.  , ,  (*). Пусть (*). Пусть  -внутр.точка обл-ти -внутр.точка обл-ти  . Построим в . Построим в  круг круг 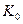 радиуса радиуса  с центром в с центром в  .Пишем ф-лу среднего для .Пишем ф-лу среднего для  и и  учтя (*): учтя (*):    (**). Т.к. (**). Т.к.  непрерывна на контуре интегрирования и из (*) непрерывна на контуре интегрирования и из (*) 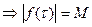 при при 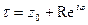 (***). По (*) (***). По (*)  не может быть не может быть  . Если предположим, что в какой-то . Если предположим, что в какой-то 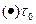 интегрирования модуль интегрирования модуль  то из непрерыв. то из непрерыв.  и в некой и в некой 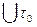 , т.е. можно указать отрезок инт-ия , т.е. можно указать отрезок инт-ия  , на котором , на котором  Тогда Тогда  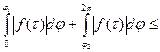   ,что противоречит (**).Значит (***) имеет место.■ ,что противоречит (**).Значит (***) имеет место.■
Теорема Лиувилля.
Пусть на всей компл.пл-ти ф-ия  аналитическая, а аналитическая, а  равномерно ограничен. Тогда равномерно ограничен. Тогда  тождественно = постоянной. □Пишем тождественно = постоянной. □Пишем  в в  : : 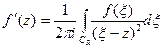 ,интегрирование будем вести по окружности ,интегрирование будем вести по окружности  . Из условия . Из условия 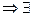 такая такая   ,что ,что  независимо от независимо от  . Поэтому . Поэтому   . Т.к. . Т.к.  можно выбрать сколь угодно большим, а можно выбрать сколь угодно большим, а  не зависит от не зависит от  . Т.к. выбираем . Т.к. выбираем  на всей компл.пл-ти. на всей компл.пл-ти.  . ■ . ■
Основная теорема алгебры
Полином 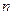 -ой степени имеет на компл.пл-ти ровно -ой степени имеет на компл.пл-ти ровно 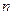 нулей (с учётом их кратности). □Представим полином нулей (с учётом их кратности). □Представим полином  в виде в виде  , где , где  , ,  . Составим . Составим  . При . При 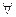 заданных значениях заданных значениях  всегда найдётся такое знач. всегда найдётся такое знач.  , что для всех знач. , что для всех знач.  имеет место: имеет место:  . По теор.Руше . По теор.Руше 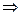 , что полное число нулей ф-ии , что полное число нулей ф-ии  в в 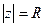 равно числу нулей в этом круге ф-ии равно числу нулей в этом круге ф-ии  . Но . Но  на всей компл.пл-ти имеет! на всей компл.пл-ти имеет! 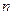 -кратный нуль - -кратный нуль - 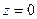 .Отсюда в силу произвольности .Отсюда в силу произвольности  и следует утверждение теоремы.■ и следует утверждение теоремы.■
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




