Равномерная сходимость рядов ФКП.
Кр.Коши: Ряд  (*) равном.сход.в обл. (*) равном.сход.в обл. 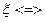 если если
 при при  натурального.□(Необх.) Из равном. сход. (*) натурального.□(Необх.) Из равном. сход. (*)   при при  , для , для  натур. (Дост.)Из натур. (Дост.)Из  (**)по кр.Коши для числ.посл-ти с компл.числами (**)по кр.Коши для числ.посл-ти с компл.числами 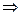 , что при , что при  -сходится.Значит, при выполнении (**) ряд (*) сход. в -сходится.Значит, при выполнении (**) ряд (*) сход. в  к к  . НО в силу (**): . НО в силу (**):  при при  во всех точках обл-ти во всех точках обл-ти  одновременно.■ одновременно.■
Непрерывность суммы равномерно сходящихся рядов ФКП.
Если ф-ии  непрерывны в обл. непрерывны в обл.  , а ряд , а ряд  сход.в ней равномерно к сход.в ней равномерно к  , то , то  непрер. в обл-ти непрер. в обл-ти  . □Рассм. . □Рассм.  , где , где  принадлежат обл. принадлежат обл.  .Т.к. равномерная сходимость ряда .Т.к. равномерная сходимость ряда  ,для ,для 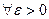 можно указать такое можно указать такое  , что имеем: , что имеем:   для для 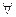 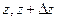 ,что ,что  .Т.к. .Т.к.  непрерна,то в непрерна,то в 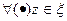 для заданного для заданного  и выбранного и выбранного  можно указать такое можно указать такое  , что , что   при при 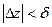 . Из всего этого . Из всего этого 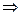 для для  можно указать можно указать  при при 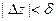 .■ .■
Почленное интегрирование равномерно сходящихся рядов ФКП.
 n(z) равномерно сходится к f(z); fn(z) аналитична в D n(z) равномерно сходится к f(z); fn(z) аналитична в D 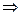  D D
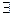  (z)dz= (z)dz=  n(z) n(z)
Un(x)-непрерывен на [a,b];  n(x) равномерно сходится к S(x) на [a,b]; n(x) равномерно сходится к S(x) на [a,b];
 n(x)dx= n(x)dx=  (x)dx; □ Un(x)-непрерывен на [a,b] (x)dx; □ Un(x)-непрерывен на [a,b]
А S(x) – непрерывна на [a,b]; (по теореме о непрерывности суммы)
1)Un(x), S(x)- непрерывны; 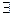 S1, S2; S1, S2;
2)  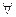 n> n> 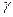 ; ; 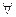 x x 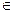 [a,b]: |S(x)-Sn(x)|< [a,b]: |S(x)-Sn(x)|< 
Полученный ряд имеет  n конечную сумму n конечную сумму  n= n=  n(x)dx n(x)dx
|  (x)dx- (x)dx-  n|=| n|=|  (x)dx- (x)dx-  n(x)dx|=| n(x)dx|=|  (x)dx - (x)dx -  n(x)dx|=| n(x)dx|=|  (x)- Sn(x)dx |<= (x)- Sn(x)dx |<= 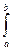 |S(x)-Sn(x)|dx< |S(x)-Sn(x)|dx<  (b-a) ■ (b-a) ■
Я теорема Вейерштрасса.
Пусть ф-ии  -аналит-ие в обл. -аналит-ие в обл.  ,а ряд ,а ряд  сход.равномерно в сход.равномерно в 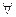 замкн. подобласти замкн. подобласти  обл-ти обл-ти  к ф-ии к ф-ии  . Тогда: 1) . Тогда: 1)  -анал.ф-я в обл. -анал.ф-я в обл.  . 2) . 2)  . 3) Ряд . 3) Ряд 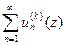 сход. равномерно в сход. равномерно в 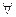 замкн. подобласти замкн. подобласти  обл-ти обл-ти  . □1) Рассм. . □1) Рассм. 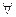 внутр. внутр.  ,построим односвяз.подобл. ,построим односвяз.подобл.  обл-ти обл-ти  ,содержащую ,содержащую  внутри. внутри.  -непрерывная ф-ия в обл-ти -непрерывная ф-ия в обл-ти  . Рассм. . Рассм. 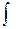 от от  по произв. контуру по произв. контуру  целиком.Т.к. в силу аналитичности целиком.Т.к. в силу аналитичности  : :  . Выполнены все усл-я т.Морера. . Выполнены все усл-я т.Морера. 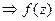 -ф-ия аналит-ая в -ф-ия аналит-ая в  точки точки  .Т.к. произвольная .Т.к. произвольная  , , 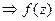 -аналитическая в -аналитическая в  ■ □2) Фиксируем ■ □2) Фиксируем  и выберем и выберем  замкн.контур замкн.контур  целиком и содержащим целиком и содержащим  внутри. Миним. расстояние от внутри. Миним. расстояние от  до до  обозначим обозначим 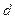 . Рассм. ряд . Рассм. ряд  . Т.к. . Т.к.  ряд сход.равном. на ряд сход.равном. на  в силу условий теоремы. Проинт.его почленно по в силу условий теоремы. Проинт.его почленно по  и используя инт-л Коши,имеем: и используя инт-л Коши,имеем: 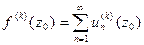 . Т.к. . Т.к.  - - 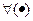 обл-ти обл-ти  ,то доказано.■ □3) Рассм. ,то доказано.■ □3) Рассм. 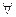 подобл-ть подобл-ть  обл-ти обл-ти  и постр.замкн.контур и постр.замкн.контур  содержащий содержащий  внутри, причём внутри, причём  . Для . Для  имеем: имеем: 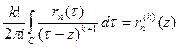 .Причём .Причём  -остаток ряда -остаток ряда  . В силу сходимости . В силу сходимости  ,для ,для 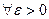 можно указать такое можно указать такое  , что на , что на  при при  будет равномерная оценка будет равномерная оценка  ,где ,где 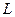 -длина контура -длина контура  .Тогда .Тогда  , что и доказывает.■ Эти доказательства для односвязной обл. , что и доказывает.■ Эти доказательства для односвязной обл.  .Для многосв.рассматривается аналогично. .Для многосв.рассматривается аналогично.
Я теорема Вейерштрасса.
Пусть ф-ии  -аналит-ие в обл. -аналит-ие в обл.  ,непрерывные в ,непрерывные в  и ряд и ряд
 сход.равномерно на границе сход.равномерно на границе 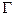 этой обл-ти.Тогда ряд этой обл-ти.Тогда ряд 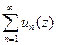 равном.сход. и в равном.сход. и в  . □Разность частичных сумм данного ряда, ф-я . □Разность частичных сумм данного ряда, ф-я  ,как конечная сумма аналит-их ф-ий, явл.аналитической в ,как конечная сумма аналит-их ф-ий, явл.аналитической в  и непрер.в и непрер.в  .Из равном.сход. .Из равном.сход. 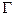 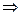   ,при ,при  для для 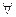 натурального натурального  и всех и всех 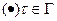 одновременно. По теор.о максимуме одновременно. По теор.о максимуме  аналит-ой ф-ии аналит-ой ф-ии  при при  для для 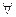 натурального натурального  и для всех и для всех  . Выполнен кр.Коши, что и доказывает теорему.■ . Выполнен кр.Коши, что и доказывает теорему.■
Теорема Абеля.
Если степенной ряд  сход. в некот. сход. в некот.  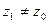 ,то он абсолютно сходится в ,то он абсолютно сходится в  ,удовлетворяющую ,удовлетворяющую  причём в причём в  радиуса радиуса 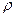  , ряд сходится равномерно.□Обозначим , ряд сходится равномерно.□Обозначим 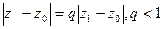 . Т.к. . Т.к.  должен сходится, то при должен сходится, то при 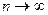 его члены его члены    . .  Тогда Тогда   (*). По условию (*). По условию 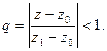  сходится. Из (*) сходится. Из (*) 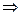 сходимость рассматриваемого ряда. Чтобы доказать равномерную сход-ть сходимость рассматриваемого ряда. Чтобы доказать равномерную сход-ть  в круге в круге  достаточно, по приз. Вайерштр., построить сходящийся числовой ряд, мажорирующий данный ряд в рассматриваемой области. Такой ряд – это достаточно, по приз. Вайерштр., построить сходящийся числовой ряд, мажорирующий данный ряд в рассматриваемой области. Такой ряд – это 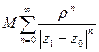 , тоже представляюет сумму бескон.геом. прогрессии со знаменателем , тоже представляюет сумму бескон.геом. прогрессии со знаменателем  ■ ■
Круг и радиус сходимости степенного ряда.

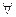   ряд сходится(круг сходимости степенного ряда, R-радиус сходимости), ряд сходится(круг сходимости степенного ряда, R-радиус сходимости), 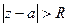 расходится. расходится. 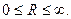


Если не 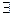 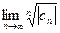  -формула Коши-Адамара. -формула Коши-Адамара.
Степенной ряд (1) внутри своего круга сходимости сходится к своей сумме f(z), которая является аналитической.
Внутри круга сходимости степенной ряд можно почленно интегрировать по любой кривой, целиком лежащей в круге сходимости и почленно дифференцировать любое количество раз, при этом вновь полученные степенные ряды будут иметь тот же радиус сходимости.
Пр. 1)  z z 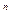  R= R= 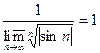 , ,  . .
Теорема Тейлора.
 , аналитическая внутри , аналитическая внутри  , может быть представлена в этом круге степ.рядом , может быть представлена в этом круге степ.рядом  , причём он определён однозначно. □Выберем , причём он определён однозначно. □Выберем  , построим окружность , построим окружность  с центром в с центром в  радиуса радиуса  . Имеем . Имеем  (*). Преобразуем: (*). Преобразуем:   (**). (**).     . .  по теор. Коши можно заменить на по теор. Коши можно заменить на 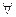 замкн.контур замкн.контур  ,лежащим в ,лежащим в  . .  , аналитическая внутри , аналитическая внутри  , разлаг.в нём в сходящийся степ. ряд. Коэф-ты разложения , разлаг.в нём в сходящийся степ. ряд. Коэф-ты разложения  . Докажем! разложения. Пусть есть другое: . Докажем! разложения. Пусть есть другое:  где хотя бы один где хотя бы один  . Ряд сход-ся в . Ряд сход-ся в  . Из всего . Из всего  .?!? .?!? 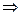 ! доказана. ■ ! доказана. ■
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




