Силы, действующие в зацеплении передач
В прямозубой передаче в зоне зацепления действует нормальная сила  , которая направлена по линии зацепления NN. Эту силу раскладывают на составляющие: окружную силу , которая направлена по линии зацепления NN. Эту силу раскладывают на составляющие: окружную силу 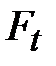 и радиальную и радиальную 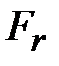 .При заданном моменте .При заданном моменте  , , 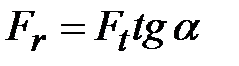 . .
Для косозубой передачи составляющие нормальной силы  (см. рис. 4.12)окружная сила (см. рис. 4.12)окружная сила 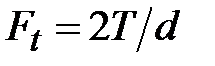 , осевая , осевая  и радиальная и радиальная  . .
В шевронной передачеосевые силы 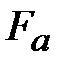 взаимно уравновешиваются и не передаются на валы и опоры. взаимно уравновешиваются и не передаются на валы и опоры.
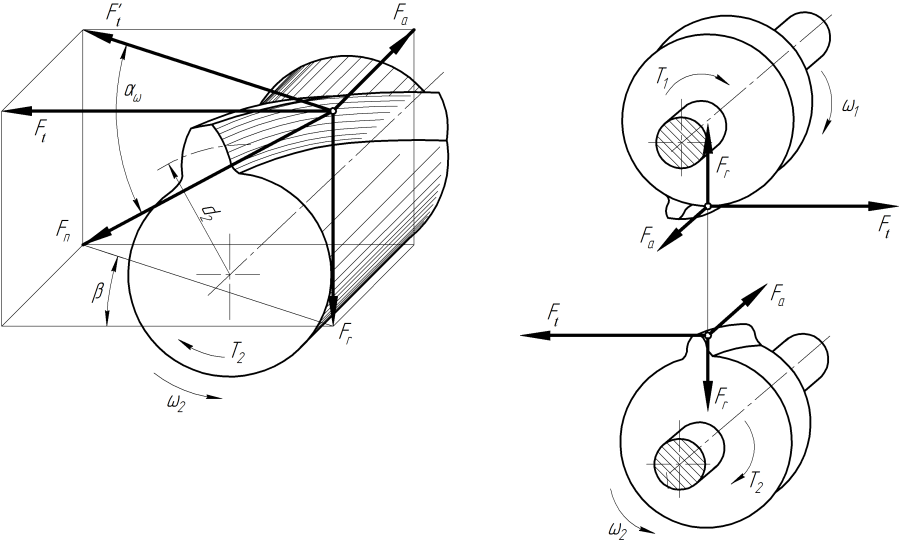
Рис. 4.12. Силы, действующие в зацеплении передач
Проверочный расчет зубьев на выносливость при изгибе
Для предотвращения усталостного излома шестерни и колеса должно выполняться условие:
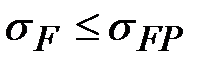 , (4.3.28) , (4.3.28)
где  – расчетное местное напряжение изгиба в опасном сечении; – расчетное местное напряжение изгиба в опасном сечении;  – допустимое напряжение. – допустимое напряжение.
Расчетное местное напряжение при изгибе определяют по формуле:
 . (4.3.29) . (4.3.29)
Коэффициент нагрузки при изгибе:
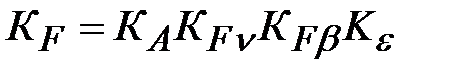 . (4.3.30) . (4.3.30)
Коэффициент  формы зуба выбирают в зависимости от числа зубьев эквивалентного колеса. Коэффициент формы зуба выбирают в зависимости от числа зубьев эквивалентного колеса. Коэффициент  , учитывающий распределение нагрузки по длине контактных линий при расчетах понапряжениям изгиба, определяют по графику (см. рис. 4.9) в зависимости от параметра , учитывающий распределение нагрузки по длине контактных линий при расчетах понапряжениям изгиба, определяют по графику (см. рис. 4.9) в зависимости от параметра  , твердости поверхностей зубьев и места установки колес относительно опор. , твердости поверхностей зубьев и места установки колес относительно опор.
Коэффициент  ,учитывающий динамическую нагрузку, можно определить по таблице 4.11 или формуле ,учитывающий динамическую нагрузку, можно определить по таблице 4.11 или формуле
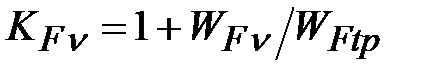 . (4.3.31) . (4.3.31)
Удельную окружную динамическую силу при изгибе принимают для дальнейших расчетов по таблице 4.10 или рассчитывают по выражению
 , (4.3.32) , (4.3.32)
где 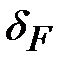 – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зубьев: для косозубых и шевронных передач – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зубьев: для косозубых и шевронных передач  = 0,06; для прямозубых передач с модификацией головки = 0,06; для прямозубых передач с модификацией головки 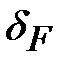 = 0,11; для прямозубых передач без модификации головки = 0,11; для прямозубых передач без модификации головки 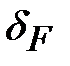 = 0,16; = 0,16;  – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса (см. табл. 4.9); – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса (см. табл. 4.9);
 – окружная скорость, м/с. – окружная скорость, м/с.
Удельную расчетную окружную силу при расчете на изгибную прочность определяют по формуле:
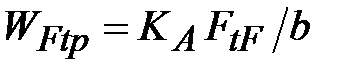 . (4.3.33) . (4.3.33)
Коэффициент 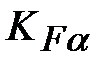 учитывает распределение нагрузки между зубьями. Для расчета на выносливость при изгибе прямозубыхпередач можно принимать учитывает распределение нагрузки между зубьями. Для расчета на выносливость при изгибе прямозубыхпередач можно принимать  . Для косозубых и шевронных передач значения . Для косозубых и шевронных передач значения  выбирают в зависимости от степени точности изготовления передачи: выбирают в зависимости от степени точности изготовления передачи:
Степень точности 6 7 8 9
 0,72 0,81 0,91 1 0,72 0,81 0,91 1
При необходимости более точного расчета 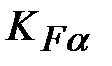 следует воспользоваться рекомендациями ГОСТ 21354 – 87. следует воспользоваться рекомендациями ГОСТ 21354 – 87.
Коэффициент, учитывающий наклон зуба:
 , (4.3.34) , (4.3.34)
где  – коэффициент осевого перекрытия. Желательно проектировать передачу так, чтобы – коэффициент осевого перекрытия. Желательно проектировать передачу так, чтобы 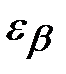 был бы близок или равен целому числу. был бы близок или равен целому числу.
Коэффициент, учитывающий перекрытие зубьев в прямозубых передачах,  ,в косозубых передачах – ,в косозубых передачах –  (при (при  ) или ) или 
(при 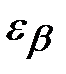 ≥1). ≥1).
Проверочный расчет на прочность по напряжениям изгиба
при перегрузках
Прочность зубьев, необходимую для предотвращения остаточных деформаций, хрупкого излома или образования первичных трещин в поверхностном слое, определяют из условия:
 , (4.3.35) , (4.3.35)
т.е. сопоставляя расчетное и допустимое напряжения изгиба в опасном сечении при максимальной нагрузке.
Расчетное напряжение изгиба в опасном сечении
 , (4.3.36) , (4.3.36)
где 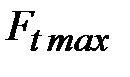 – максимальная нагрузка; – максимальная нагрузка;  – рабочая нагрузка. – рабочая нагрузка.
Ориентировочно можно принимать 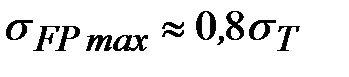 при НВ <350 и при НВ <350 и  при НВ > 350 (здесь при НВ > 350 (здесь  – предел текучести материала). – предел текучести материала).
4.4. Расчет конических передач
Конические зубчатые передачи применяются при необходимости передачи вращающего момента между валами, оси которых пересекаются. Угол между осями обычно равен 90°. Но возможен угол и отличный от 90°.
Конические колеса выполняются с прямыми, тангенциальными, круговыми и другими криволинейными зубьями (рис. 4.13).
По сравнению с цилиндрическими зубчатыми передачами, конические имеют большую массу и габаритные размеры, дороже в изготовлении и требуют тщательной регулировки закрепления при монтаже и в процессе эксплуатации. Кроме того, в коническом зацеплении возникают осевые силы, дополнительно нагружающие подшипники. Нагрузочная способность конической прямозубой передачи приблизительно на 15 % ниже цилиндрической.

Рис. 4.13. Виды конических зубчатых колес с прямыми а,
тангенциальными б и круговыми в зубьями
Область применения конических колес с прямыми зубьями ограничена окружной скоростью до 3 м/с. Колеса с косыми (тангенциальными) зубьями используют редко, так как они очень чувствительны к погрешностям изготовления и монтажа и трудоемки в изготовлении. При окружных скоростях более 3 м/с в основном применяют зубчатые колеса с круговыми зубьями. Они проще в изготовлении, менее чувствительны к погрешностям изготовления и монтажа. Их зубья обладают высокой изгибной прочностью, а передачи с такими колесами – большой плавностью зацепления. Существенный недостаток передач с косыми и круговыми зубьями – возникающие в них осевые усиления, которые при изменении направления вращения колес меняются по значению и направлению.
Основные кинетические и геометрические параметры. В зависимости от размеров сечений по длине зубья конических колес выполняют трех форм
(рис. 4.14).
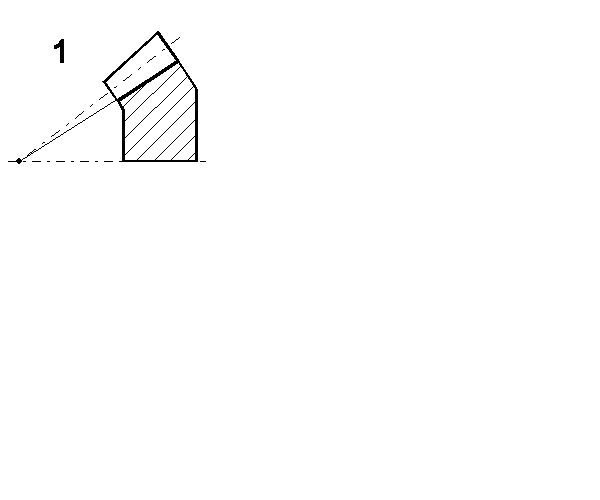   
Рис. 4.14. Формы зубьев конических колес
Осевую форму 1 применяют для конических передач с прямыми и тангенциальными (косыми) зубьями, а также для передач с круговыми зубьями при нормальном модуле 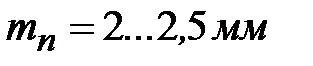 , угле наклона линии зуба на среднем диаметре , угле наклона линии зуба на среднем диаметре  °и общем числе зубьев °и общем числе зубьев 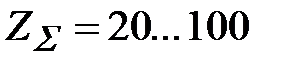 .Для этой формы характерны нормальные понижающиеся зубья и совпадения вершин делительного и внутреннего конусов. .Для этой формы характерны нормальные понижающиеся зубья и совпадения вершин делительного и внутреннего конусов.
Осевая форма 2 характеризуется равноширокими зубьями и несовпадением вершин делительного и внутреннего конусов. При такой форме ширина впадины постоянная, а толщина зуба по делительному конусу увеличивается пропорционально расстоянию от вершины. Это основная форма для колес с круговыми зубьями, так как позволяет обрабатывать одновременно обе поверхности зубьев.
Осевой форме 3 присущи равновысокие зубья, так как образующие делительного и внутреннего конусов параллельны между собой. Такую форму применяют для круговых зубьев при  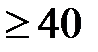 и средних конусных расстояниях и средних конусных расстояниях
от 75 до 750 мм.
Для конических колес удобнее задавать и измерять размеры зубьев на внешнем торце. Так, в колесах с зубьями формы I задают внешний окружной модуль  , значение которого может быть нестандартное. В конических колесах с зубьями формы II принято применять нормальный модуль , значение которого может быть нестандартное. В конических колесах с зубьями формы II принято применять нормальный модуль 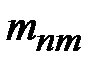 на середине ширины зубчатого венца. на середине ширины зубчатого венца.
Для нарезания круговых зубьев используют немодульный инструмент, позволяющий обрабатывать зубья в некотором диапазоне модулей.
Поэтому допускается использование передач с нестандартными и даже дробными модулями.
Между модулями  и и 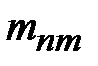 существует следующая зависимость: существует следующая зависимость:
 , (4.4.1.) , (4.4.1.)
где  – коэффициент относительной ширины колеса; b – ширина зубчатого венца; – коэффициент относительной ширины колеса; b – ширина зубчатого венца;  – внешнее конусное расстояние; – внешнее конусное расстояние;  – угол наклона линии – угол наклона линии
зуба.
При выборе  следует помнить, что его увеличение улучшает плавность зацепления, но при этом возрастает осевое усиление зацепления, и, как следствие, увеличиваются габаритные размеры подшипниковых узлов. Для трансмиссий обычно применяют следует помнить, что его увеличение улучшает плавность зацепления, но при этом возрастает осевое усиление зацепления, и, как следствие, увеличиваются габаритные размеры подшипниковых узлов. Для трансмиссий обычно применяют  . .
При ведущей шестерне конические передачи выполняют, как правило, с передаточным отношением 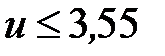 . В передачах с круговыми зубьями предельное значение . В передачах с круговыми зубьями предельное значение 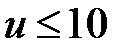 . Если шестерня ведомая, то передаточное отношение должно быть не более 3,15. . Если шестерня ведомая, то передаточное отношение должно быть не более 3,15.
Число зубьев шестерни обычно задают в пределах 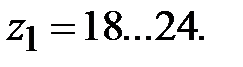 Минимальное число зубьев шестерни конических передач, при котором отсутствует подрезание зубьев, определяют по формулам: для прямозубых передач с исходным контуром по ГОСТ 13754-81: Минимальное число зубьев шестерни конических передач, при котором отсутствует подрезание зубьев, определяют по формулам: для прямозубых передач с исходным контуром по ГОСТ 13754-81:
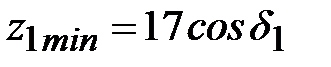 . (4.4.2) . (4.4.2)
Для передач с круговыми зубьями при выполнении исходного контура по ГОСТ 16202-81:
 , (3.4.3) , (3.4.3)
где  – половина угла делительного конуса. – половина угла делительного конуса.
Для выбора  в конических передачах рекомендуется: для зубчатых передач с твердостью рабочих поверхностей зубьев шестерни и колеса в конических передачах рекомендуется: для зубчатых передач с твердостью рабочих поверхностей зубьев шестерни и колеса  число зубьев шестерни определяется по графикам на рис. 4.15 в зависимости от внешнего делительного диаметра шестерни число зубьев шестерни определяется по графикам на рис. 4.15 в зависимости от внешнего делительного диаметра шестерни  . .

Рис. 4.15. Графики для определения зубьев конической шестерни
а – прямозубой; б – с круговыми зубьями
Схема сил, действующих в прямозубом коническом зацеплении приведена на рис. 4.16, а, б, в геометрические размеры конического зацепления – на
рис. 4.16, г.


а) б)
Рис. 4.16. Схема сил, действующих в прямозубом коническом зацеплении,
и геометрические размеры конического зацепления
Таблица 4.14
Условные обозначения и основные формулы геометрического расчета
параметров ортогональной конической передачи
с круговыми зубьями, изготовленными по форме 1
| Параметр
| Обозначения и расчетные формулы
| |
|
| | 1. Число зубьев плоского колеса
| 
| | 2. Среднее конусное расстояние
| 
| | 3. Внешнее конусное расстояние
| 
| | 4. Ширина зубчатого венца
| b
| | 5. Среднее конусное расстояние для зубьев
| 
| | 6. Коэффициент ширины
| 
| | 7. Средний нормальный модуль зубьев
| 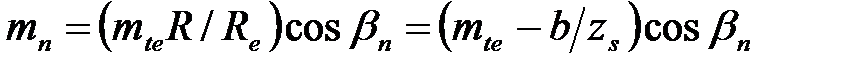
| | 8. Передаточное число
| u = z2 / z1
| | 9. Угол делительного конуса
| Шестерня
| 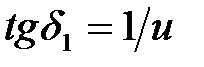
| | Колесо
| 
| | 10. Коэффициент смещения
| Шестерня
| 
| | Колесо
| 
| | 11. Коэффициент изменения толщины зубьев шестерни
| 
| | 12. Внешний окружной модуль при заданном
| 
| | 13. Высота ножки зуба в расчетном сечении, мм
| Шестерня
| 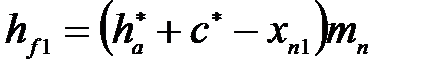
| | Колесо
| 
| | 14. Нормальная толщина зу-ба в расчетном сечении
| Шестерня
| 
| | Колесо
| 
| | 15. Угол ножки зубьев
| Шестерня
| 
| | Колесо
| 
| | 16. Угол головки зубьев
| Шестерня
| 
| | Колесо
| 
| | 17. Увеличение высоты головки зуба при переходе от среднего сечения на внешний торец
| Шестерня
| 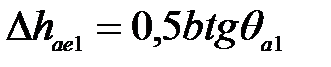
| | Колесо
| 
| | 18. Увеличение высоты ножки зуба при переходе от расчетного сечения на внешний торец
| Шестерня
| 
| | Колесо
| 
| | 19. Высота головки зуба в расчетном сечении
| Шестерня
| 
| | Колесо
| 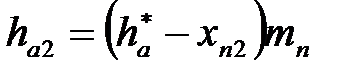
| | 20. Внешняя высота головки зуба
| Шестерня
| 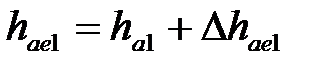
| | Колесо
| 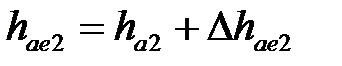
| | | | | | Окончание табл. 4.14
|
|
| | 21. Внешняя высота ножки зуба
| Шестерня
| 
| |
| Колесо
| 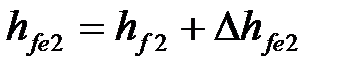
| | 22. Внешняя высота зуба
| Шестерня
| 
| | Колесо
| 
| | 23. Угол конуса вершин
| Шестерня
| 
| | Колесо
| 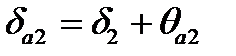
| | 24. Угол конуса впадин
| Шестерня
| 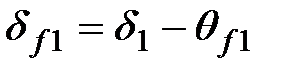
| | Колесо
| 
| | 25.Средний делительный диаметр
| Шестерня
| 
| | Колесо
| 
| | 26. Внешний делительный диаметр
| Шестерня
| 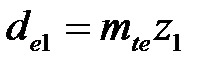
| | Колесо
| 
| | 27. Внешний диаметр вершин
| Шестерня
| 
| | Колесо
| 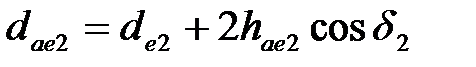
| | 28. Расстояние от вершины до плоскости внешней окружности вершин зубьев
| Шестерня
| 
| | Колесо
| 
| | 29. Коэффициент осевого перекрытия
| 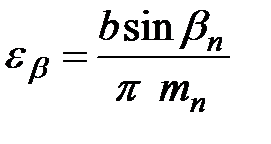
|
При твердости  ≤350 и ≤350 и  ≤350 значение ≤350 значение 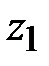 , определенное по графику, увеличивают в 1,6 раза; при , определенное по графику, увеличивают в 1,6 раза; при  и и  ≤350 – в 1,3 раза. ≤350 – в 1,3 раза.
Подробный расчет для прямозубых конических передач приведен в
ГОСТ 19624-74, а для колес с круговыми зубьями – в ГОСТ 19326-73.
Основные зависимости для определения геометрических параметров ортогональной конической передачи с круговыми зубьями, изготовленными по форме 1 и форме 2, указаны в таблицах 4.14. и 4.15.
Таблица 4.15
Основные формулы геометрического расчета параметров ортогональной
конической передачи с круговыми зубьями, изготовленными по форме 2
| Параметр
| Обозначения и расчетные формулы
| |
|
| | 1. Число зубьев плоского колеса
| 
| | 2. Внешнее конусное расстояние
| 
| | 3. Ширина зубчатого венца
| b
| | 4. Среднее конусное расстояние для зубьев
| R = Re - 0,5b
| | 5. Коэффициент ширины
| 
| | 6. Средний угол наклона линии зубьев
| sin n = (d 0/2 R)(1 – 0.5 b 2/ d 02)
| | 6. Средний нормальный модуль зубьев
| 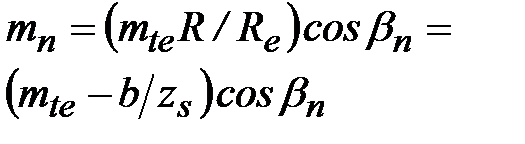
| | 6. Передаточное число
| u = z2 / z1
| | 7. Угол делительного конуса
| Шестерня
| 
| | Колесо
| 
| | 8. Коэффициент смещения
| Шестерня
| xn1 = 2(1-1 /u 2)cos3 bn/z1)1/2
| | Колесо
| 
| | 9. Коэффициент изменения толщины зубьев шестерни
| 
| | 10. Внешний окружной модуль при заданном
| 
| | 11. Сумма углов ножек шестерни и колеса
|  , где , где 
 ; ; 
| | 12. Угол ножки зубьев
| Шестерня
| 
| | Колесо
| 
| | 13. Угол головки зубьев
| Шестерня
| 
| | Колесо
| 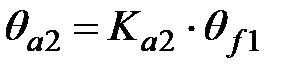
| | 14. Высота ножки зуба в расчетном сечении, мм
| Шестерня
| 
| | Колесо
| 
| | 15. Увеличение высоты головки зуба при переходе от среднего сечения на внешний торец
|
Шестерня
| 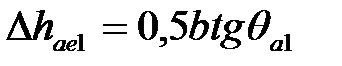
| |
Колесо
| 
| | 16. Увеличение высоты ножки зуба при переходе от расчетного сечения на внешний торец
| Шестерня
| 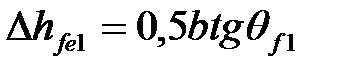
| | Колесо
| 
| | 17. Уменьшение высоты головки зуба в расчетном режиме
| Шестерня
| 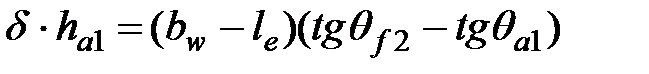
| | Колесо
| 
| | | | | | Окончание табл. 4.15
|
|
| | 18. Высота головки зуба в расчетном сечении
| Шестерня
| 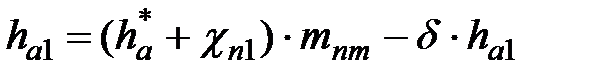
| | Колесо
| 
| | 19. Внешняя высота головки зуба
| Шестерня
| 
| | Колесо
| 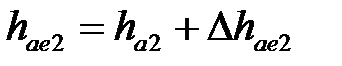
| | 20. Внешняя высота ножки зуба
| Шестерня
| 
| | Колесо
| 
| | 21. Внешняя высота зуба
| Шестерня
| 
| | Колесо
| 
| | 22. Угол конуса вершин
| Шестерня
| 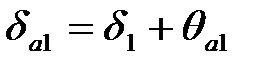
| | Колесо
| 
| | 23. Угол конуса впадин
| Шестерня
| 
| | Колесо
| 
| | 24. Средний делительный диаметр
| Шестерня
| 
| | Колесо
| 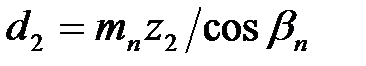
| | 25. Внешний делительный диаметр
| Шестерня
| 
| | Колесо
| 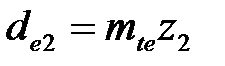
| | 26. Внешний диаметр вершин
| Шестерня
| 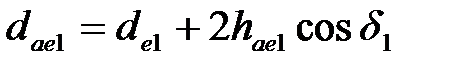
| | Колесо
| 
| | 27. Расстояние от вершины до плоскости внешней окружности вершин зубьев
| Шестерня
| 
| | Колесо
| 
| | 28. Коэффициент осевого перекрытия
| 
|
В конических передачах  >1; чтобы повысить сопротивление заеданию в зацеплении, шестерню рекомендуется выполнять с положительным смещением ( >1; чтобы повысить сопротивление заеданию в зацеплении, шестерню рекомендуется выполнять с положительным смещением ( для прямозубых передач, для прямозубых передач,  для передач с круглыми зубьями), а колесо – с равным ему по абсолютной величине отрицательным смещением для передач с круглыми зубьями), а колесо – с равным ему по абсолютной величине отрицательным смещением
( или или  ). ).
Значение  и и  определяют по таблицам ГОСТ 19624-74, определяют по таблицам ГОСТ 19624-74,
ГОСТ 19326-73 или по формуле
 . (4.4.4) . (4.4.4)
Для конических зацеплений с  ≥2,5 применяют тангенциальную коррекцию, за счет которой увеличивается толщина зуба шестерни при соответственном уменьшении толщины зуба колеса, что приводит к выравниванию их прочности на изгиб. Коэффициент тангенциального смещения (изменения расчетной толщины зуба исходного контура): ≥2,5 применяют тангенциальную коррекцию, за счет которой увеличивается толщина зуба шестерни при соответственном уменьшении толщины зуба колеса, что приводит к выравниванию их прочности на изгиб. Коэффициент тангенциального смещения (изменения расчетной толщины зуба исходного контура):
 , (4.4.5) , (4.4.5)
где a, b – постоянные коэффициенты, характеризующие инструмент: a = 0,03,
b = 0,08 для прямозубых передач; а = 0,11, b = 0,01 для передач с круговыми зубьями – при βm =35°.
Тангенциальная коррекция не требует специального инструмента, ее выполняют разведением резцов, обрабатывающих противоположные стороны зубьев. Применение высотной коррекции в сочетании с тангенциальной позволяет одновременно уменьшить вероятность заедания зубьев и выровнять прочность зубьев шестерни и колеса.
Проектный и проверочный расчеты конических передач
на контактную выносливость
По критериям эти расчеты аналогичны расчетам цилиндрических передач, отличаются лишь уточнением некоторых коэффициентов и определением внешнего делительного диаметра колеса вместо межосевого расстояния.
Для прямозубых конических колес и колес с круговыми зубьями при
βm = 35° и  = 0,285 ориентировочное значение внешнего делительного диаметра = 0,285 ориентировочное значение внешнего делительного диаметра  , мм, можно определить по формуле , мм, можно определить по формуле
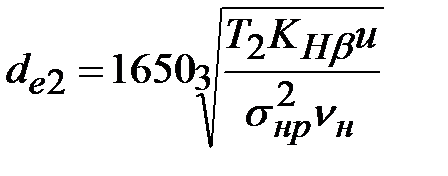 . (4.4.6) . (4.4.6)
где  – расчетный вращающий момент на колесе, Н – расчетный вращающий момент на колесе, Н 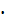 м; м;  – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца зубчатого колеса. Для конических передач коэффициент – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца зубчатого колеса. Для конических передач коэффициент 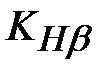 можно определятьпо графикам (см. рис. 4.9) при можно определятьпо графикам (см. рис. 4.9) при  = 0,285; u – передаточное число, должно соответствовать одному из стандартных значений; = 0,285; u – передаточное число, должно соответствовать одному из стандартных значений;  – допустимое контактное напряжение, МПа; – допустимое контактное напряжение, МПа; 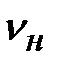 – коэффициент вида зубьев: для конических передач с прямым зубом – коэффициент вида зубьев: для конических передач с прямым зубом  = 0,85; для передач с круговым зубом его определяют по формулам таблицы 4.16. = 0,85; для передач с круговым зубом его определяют по формулам таблицы 4.16.
Таблица 4.16
Формулы для определения коэффициентов  и и 
| Коэффициент
| Твердость рабочих поверхностей зубьев
| HB  , HB , HB 
| HRC 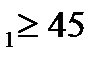 ,HB ,HB 
| HRC  ,НRC ,НRC 
| 
|  =1,22+0,21u =1,22+0,21u
|  =1,13+0,13u =1,13+0,13u
|  =0,81+0,15u =0,81+0,15u
| 
|  =0,94+0,08u =0,94+0,08u
|  =0,85+0,043u =0,85+0,043u
|  =0,65+0,11u =0,65+0,11u
|
Полученное значение  округляют до стандартного, по которому выбирают ширину венцов колес (табл. 4.17). округляют до стандартного, по которому выбирают ширину венцов колес (табл. 4.17).
Затем определяют внешний делительный диаметр шестерни  ,и по графикам (см. рис. 4.15) определяют число зубьев шестерни z 1ичисло зубьев колеса ,и по графикам (см. рис. 4.15) определяют число зубьев шестерни z 1ичисло зубьев колеса  . Полученное число зубьев . Полученное число зубьев 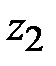 округляют до целого числа в ближайшую сторону и уточняют фактическое передаточное число: округляют до целого числа в ближайшую сторону и уточняют фактическое передаточное число:  . .
Отклонение расчетного значения и от заданного не должно превышать 4 %.
С точностью до второго знака после запятой определяют внешний окружной модуль для колес:
– с прямыми зубьями
 ; (4.4.7) ; (4.4.7)
– с круговыми зубьями
 . (4.4.8) . (4.4.8)
Все остальные геометрические размеры вычисляют по формулам, приведенным в таблицах 4.14 и 4.15.
После определения геометрических параметров колес и передачи в целом их проверяют на контактную выносливость по формуле:
 . (4.4.9) . (4.4.9)
Таблица 4.17
Основные параметры конических передач (по ГОСТ 12289-76)
Внешний
делитель-
ный диаметр
колеса 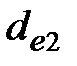
| Ширина венцов зубчатых колёс  , мм,
для номинальных передаточных чисел , мм,
для номинальных передаточных чисел
| | 1,6
| (1,8)
| 2,0
| (2,24)
| 2,5
| (2,8)
| 3,15
| (3,55)
| 4,0
| (4,5)
| 5,0
| |
(71)
(90)
(112)
(140)
(180)
(225)
(280)
| 10,5
|
11,5
|
11,5
| –
–
| –
–
| –
–
–
–
| –
–
–
–
| –
–
–
–
–
–
| –
–
–
–
–
–
| –
–
–
–
–
–
–
| –
–
–
–
–
–
–
| | Примечание: Значения диаметров, данные в скобках, ограничены в применении
|
Параметры, входящие в эту формулу, определяют следующим образом:  по рисунку 4.10; по рисунку 4.10; 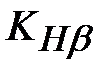 по рисунку 4.17; по рисунку 4.17;  по таблице 4.11; по таблице 4.11; 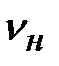 по таблице 4.16. Коэффициент по таблице 4.16. Коэффициент  , учитывающий механические свойства материала шестерни и колеса, для стали равен 190 МПа. Коэффициент , учитывающий механические свойства материала шестерни и колеса, для стали равен 190 МПа. Коэффициент  учитывающий форму сопряженных поверхностей, вычисляют по формуле (4.3.14). Для колес с прямыми зубьями можно принимать учитывающий форму сопряженных поверхностей, вычисляют по формуле (4.3.14). Для колес с прямыми зубьями можно принимать  = 2,5; с круговыми зубьями (при β m =35° = 2,5; с круговыми зубьями (при β m =35°  =2,26). =2,26).
Коэффициент, учитывающий суммарную длину контактных линий:
– для прямозубых конических передач
 , (4.4.10) , (4.4.10)
– для конических передач с круговыми зубьями
 . (4.4.11) . (4.4.11)
Коэффициент торцевого перекрытия зубьев εa вычисляют по формуле (4.3.18).
Проектный расчет конических зубчатых передач
на выносливость зубьев по напряжениям изгиба
Такой расчет выполняют для открытых передач, подверженных интенсивному износу. Сначала определяют модуль при предварительно принятом числе зубьев z 1 и параметре  . .
Рекомендуется 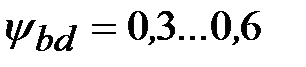 при соблюдении условий: при соблюдении условий: 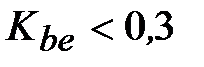 ; ;  . Меньшие значения . Меньшие значения 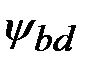 целесообразно принимать для неприрабатывающихся колес, когда HB > 350 и НВ > 350, а также при резко переменных нагрузках. целесообразно принимать для неприрабатывающихся колес, когда HB > 350 и НВ > 350, а также при резко переменных нагрузках.
Коэффициент ширины зубчатого венца относительно среднего диаметра шестерни можно также вычислить по формуле:
 . (4.4.12) . (4.4.12)
Нормальный модуль в среднем сечении зубчатого венца определяют из условия изгибной выносливости:
 , (4.4.13) , (4.4.13)
где  – допустимый коэффициент износа: – допустимый коэффициент износа:  = 1,1…1,25 в зависимости от требуемой точности передачи. = 1,1…1,25 в зависимости от требуемой точности передачи.
Для колес с круговыми зубьями такой расчет не выполняют, так как в открытых передачах эти колеса не применяют.



Рис. 4.17. Графики для определения ориентировочных значений K Hβ и K Fβ
для конических передач:1 – передача I (опоры на шариковых подшипниках);
2 – передача I (опоры на роликовых подшипниках); 3 – передача II.
Штрихпунктирные линии соответствуют коническим передачам с круговыми зубьями. Для этих передач при HB2 < 350, а также при HB1 < 350 и HB2 < 350 следует принимать K Hβ = 1
Проверочный расчет конических зубчатых передач
на выносливость по напряжениям изгиба
Напряжение изгиба в зубе шестерни:
 . (4.4.14) . (4.4.14)
Коэффициент  , учитывающий перекрытие зубьев, для конических передач с прямыми зубьями принимают , учитывающий перекрытие зубьев, для конических передач с прямыми зубьями принимают 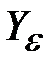 =1, а с круговыми зубьями определяют по формуле: =1, а с круговыми зубьями определяют по формуле:
 . (4.4.15) . (4.4.15)
Коэффициент, учитывающий наклон линии зуба, для конических передач с прямыми зубьями принимают  =1, с круговыми зубьями (при βm = 35°): =1, с круговыми зубьями (при βm = 35°):
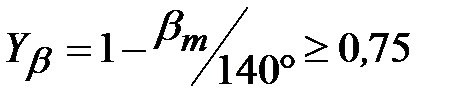 . (4.4.16) . (4.4.16)
Окружная сила на среднем диаметре, Н:
 . (4.4.17) . (4.4.17)
Коэффициент  учитывает распределение нагрузки между зубьями. Для конических передач с прямыми зубьями принимают учитывает распределение нагрузки между зубьями. Для конических передач с прямыми зубьями принимают  =1, с круговыми зубьями его определяют в зависимости от степени точности изготовления колес и окружной скорости, м/с: =1, с круговыми зубьями его определяют в зависимости от степени точности изготовления колес и окружной скорости, м/с:
 . (4.4.18) . (4.4.18)
Коэффициент  , учитывающий неравномерность распределения нагрузки по длине контактных линий, определяют по графикам (см. рис. 4.17), а коэффициент , учитывающий неравномерность распределения нагрузки по длине контактных линий, определяют по графикам (см. рис. 4.17), а коэффициент  , учитывающий динамическую нагрузку, возникающую в зацеплении, – по таблице 4.11. , учитывающий динамическую нагрузку, возникающую в зацеплении, – по таблице 4.11.
При известном напряжении  для зуба шестерни условие прочности для зуба колеса имеет вид для зуба шестерни условие прочности для зуба колеса имеет вид
 , (4.4.19) , (4.4.19)
где YFE2 – коэффициент, учитывающий форму зуба колеса. Его определяют по соотношениям, указанным табл. 4.13 или графику (см. рис. 4.11) в зависимости от числа зубьев эквивалентного колеса  и коэффициента смещения χ. и коэффициента смещения χ.
Силы, действующие в зацеплении конических зубчатых передач
В прямозубой конической передаче силу нормального давления Fn можно разложить на две составляющие (рис. 4.16, а):окружную Fn и распорную которую, всвою очередь, раскладывают на осевую Fa и радиальную Fr силы. Из рисунка 4.16, б видно,что
 ; (4.4.20) ; (4.4.20)
 , ,
где  – окружная сила соответственно на шестерне и колесе (табл. 4.18); – окружная сила соответственно на шестерне и колесе (табл. 4.18);  , ,  – вращающие моменты соответственно на шестерне и колесе. – вращающие моменты соответственно на шестерне и колесе.
Таблица 4.18
Формулы для определения сил в зацеплении
| Сила
| Ведущее зубчатое колесо
| Ведомое зубчатое колесо
| | Окружная
| 
| | Осевая
| 
| 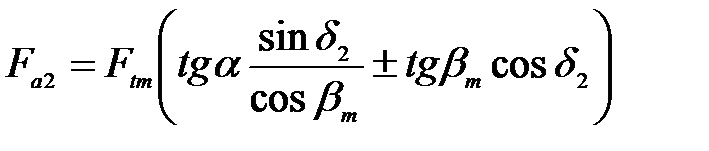 |
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|





