Сушка в условиях внутренней задачи
Постановка задачи
Сушка в условиях внутренней задачи может протекать только при удалении связанной влаги. Зерна (частицы) материала в ПС очень невелики по размерам, поэтому протяженность пути диффундирующей влаги внутри зерна мала; можно было бы предположить, что рассматриваемая стадия — быстрая и не может стать лимитирующей. Однако для ряда ТМ коэффициент внутренней диффузии влаги  крайне низок (скажем, для воды в полимерных материалах он находится на уровне 10-12 – 10-13 м2/с); поэтому внутренняя диффузия вполне может оказаться лимитирующей стадией несмотря на малые размеры частиц. крайне низок (скажем, для воды в полимерных материалах он находится на уровне 10-12 – 10-13 м2/с); поэтому внутренняя диффузия вполне может оказаться лимитирующей стадией несмотря на малые размеры частиц.
Процесс сушки в условиях внутренней задачи сначала рассмотрим качественно. Будем оперировать смешанной концентрацией влаги в материале 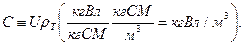 Проследим за процессом в единичном зерне, приняв его в целях упрощения сферическим, а процесс сушки — симметричным (рис. 11.46). Пусть исходная влажность материала Проследим за процессом в единичном зерне, приняв его в целях упрощения сферическим, а процесс сушки — симметричным (рис. 11.46). Пусть исходная влажность материала  постоянна по объему зерна, а равновесная (с потоком СА) составляет постоянна по объему зерна, а равновесная (с потоком СА) составляет  . После внесения зерна в зону сушки на его поверхности мгновенно (в условиях внутренней задачи внешний массообмен подразумевается бесконечно интенсивным) устанавливается и в ходе всего процесса поддерживается равновесная концентрация . После внесения зерна в зону сушки на его поверхности мгновенно (в условиях внутренней задачи внешний массообмен подразумевается бесконечно интенсивным) устанавливается и в ходе всего процесса поддерживается равновесная концентрация  . Спустя небольшой промежуток времени . Спустя небольшой промежуток времени  приповерхностные области зерна теряют влагу (глубинные — еще не затронуты сушкой). К моменту приповерхностные области зерна теряют влагу (глубинные — еще не затронуты сушкой). К моменту  незатронутыми остаются лишь центральные зоны, в остальных влажность заметно меньше. А к моменту незатронутыми остаются лишь центральные зоны, в остальных влажность заметно меньше. А к моменту  концентрация влаги меньше исходной уже во всем объеме зерна; в момент концентрация влаги меньше исходной уже во всем объеме зерна; в момент  обезвоживание зерна еще глубже: влажность понижена, она стала ближе к равновесной. Если сушка ведется долго (теоретически — бесконечно долго), то влажность во всем объеме зерна стремится к равновесной. обезвоживание зерна еще глубже: влажность понижена, она стала ближе к равновесной. Если сушка ведется долго (теоретически — бесконечно долго), то влажность во всем объеме зерна стремится к равновесной.
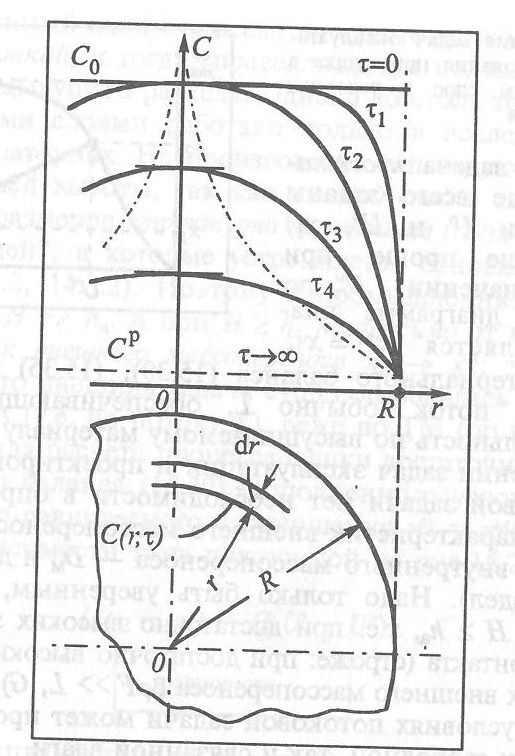
Рис. 11.46. К анализу симметричной сушки сферического зерна в условиях внутренней задачи
Задача анализа применительно к единичному зерну состоит в определении влажности в произвольной точке внутри зерна (на радиальной координате  ) в произвольный момент времени ) в произвольный момент времени  . .
Задача анализа применительно к псевдоожиженному слою заключается в учете поведения единичного зерна в массе зерен. Для ПС анализ облегчается тем, что зерна (частицы) в нем практически находятся в режиме идеального перемешивания, для которого распределение их по времени пребывания выражается относительно просто.
Представленная качественная картина должна быть интерпретирована количественно. В основе анализа лежит уравнение Фика. Для единичного сферического зерна радиусом  при симметричной сушке в случае постоянного коэффициента диффузии влаги в материале ( при симметричной сушке в случае постоянного коэффициента диффузии влаги в материале ( ) в отсутствие химических превращений (Источников и Стоков) оно записывается в сферических координатах: ) в отсутствие химических превращений (Источников и Стоков) оно записывается в сферических координатах:
  (11.36) (11.36)
Применительно к теплопереносу, для анализа и решения это уравнение более удобно в форме:
 (11.36а) (11.36а)
Коэффициент диффузии влаги в материале  нередко существенно зависит от ее концентрации в нем: при изменении нередко существенно зависит от ее концентрации в нем: при изменении  могут изменяться физическое состояние влаги в материале и характеристики ее диффузии. В этом случае могут изменяться физическое состояние влаги в материале и характеристики ее диффузии. В этом случае  нельзя считать постоянным в ходе процесса сушки (по объему зерна — тоже). Тогда усложняется написание уравнения Фика даже при достаточно простых зависимостях нельзя считать постоянным в ходе процесса сушки (по объему зерна — тоже). Тогда усложняется написание уравнения Фика даже при достаточно простых зависимостях  решение такого нелинейного уравнения Фика возможно, как правило, только численными методами. Дополнительное затруднение — в установлении и математическом выражении зависимости решение такого нелинейного уравнения Фика возможно, как правило, только численными методами. Дополнительное затруднение — в установлении и математическом выражении зависимости  от от  . .
Уравнению (11.36а) должны сопутствовать три условия однозначности (поскольку в него входит первая производная по  и вторая — по и вторая — по  ): ):
— начальное условие (чтобы подчеркнуть, что речь идет о ситуации до начала процесса, иногда вместо  пишут пишут  ): исходная концентрация влаги в объеме зерна (на любой радиальной координате ): исходная концентрация влаги в объеме зерна (на любой радиальной координате  ) равна ) равна  , так что , так что
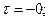   (11.37) (11.37)
— граничное условие I рода (оно отвечает внутренней задаче): в любой момент времени концентрация влаги на поверхности зерна есть равновесная концентрация, тогда
 (11.38) (11.38)
— условие симметрии сушки и ограниченности изменения концентрации влаги (по существу это тоже граничное условие):
 (11.39) (11.39)
Справедливость последнего условия ясна из рис. 11.46: касательная к любой кривой изменения концентраций  , проведенная в центре сферического зерна, горизонтальна, т.е. параллельна оси , проведенная в центре сферического зерна, горизонтальна, т.е. параллельна оси  иначе: тангенс угла наклона касательной к оси абсцисс (производная) равен нулю. Это условие характерно для симметричной сушки, в противном случае экстремум пришелся бы на какую-нибудь точку с иначе: тангенс угла наклона касательной к оси абсцисс (производная) равен нулю. Это условие характерно для симметричной сушки, в противном случае экстремум пришелся бы на какую-нибудь точку с  . Одновременно это условие запрещает безграничное (в том числе симметричное) возрастание концентрации в ходе процесса, например при асимптотическом приближении линий . Одновременно это условие запрещает безграничное (в том числе симметричное) возрастание концентрации в ходе процесса, например при асимптотическом приближении линий 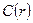 к вертикали к вертикали  (штриховые линии на рис. 11.46). (штриховые линии на рис. 11.46).
Зависимость  целесообразно для большей общности представить в критериальной форме. Критерии подобия формируются методом масштабных преобразований; проведем их в упрощенном варианте, сопоставив величины в левой и правой частях уравнения Фика: целесообразно для большей общности представить в критериальной форме. Критерии подобия формируются методом масштабных преобразований; проведем их в упрощенном варианте, сопоставив величины в левой и правой частях уравнения Фика:
 (д) (д)
После сокращения на С и переноса всех оставшихся величин в одну часть равенства-сопоставления (д) получим безразмерный комплекс  . Этот комплекс неудобен: он содержит сразу две независимые переменны - . Этот комплекс неудобен: он содержит сразу две независимые переменны -  и и  . Поэтому его преобразуют: . Поэтому его преобразуют:
 (е) (е)
Каждая из полученных безразмерных величин  и и  содержит по одной переменной. Комплекс содержит по одной переменной. Комплекс  выражает соотношение количеств вещества (влаги), переносимого диффузией и аккумулированного зерном; его называют диффузионным критерием Фурье или критерием Фика; иногда его трактуют как безразмерное время. Симплекс выражает соотношение количеств вещества (влаги), переносимого диффузией и аккумулированного зерном; его называют диффузионным критерием Фурье или критерием Фика; иногда его трактуют как безразмерное время. Симплекс  представляет собой безразмерную координату; он может изменяться от 0 до 1. Таким образом, в результате решения уравнения Фика концентрация получается в виде функции от представляет собой безразмерную координату; он может изменяться от 0 до 1. Таким образом, в результате решения уравнения Фика концентрация получается в виде функции от  и и  . Очевидно, концентрацию также резонно представить в безразмерной форме. Анализ приводит к обобщенному концентрационному комплексу . Очевидно, концентрацию также резонно представить в безразмерной форме. Анализ приводит к обобщенному концентрационному комплексу  , изменяющемуся от 1 в начале процесса сушки зерна (когда , изменяющемуся от 1 в начале процесса сушки зерна (когда 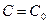 ) до 0, если сушка ведется бесконечно долго (тогда ) до 0, если сушка ведется бесконечно долго (тогда  ). Итак, решение уравнения Фика для симметричной сушки сферического зерна должно привести к зависимости в обобщенной форме: ). Итак, решение уравнения Фика для симметричной сушки сферического зерна должно привести к зависимости в обобщенной форме:
 (11.40) (11.40)
Подчеркнем, что (11.40) подлежит конкретизации.
Решение задачи
Единичное зерно. Для переноса вещества (влаги) при сушке такая зависимость имеет вид бесконечного ряда:
 (11.41) (11.41)
где  — индекс суммирования. — индекс суммирования.
Для наглядности выпишем первые члены рассматриваемого разложения:
 (е) (е)
Ряд (11.41) быстро сходится (при не очень малых значениях  ), так как от слагаемого к слагаемому быстро нарастает величина ), так как от слагаемого к слагаемому быстро нарастает величина  , стоящая в экспоненте. , стоящая в экспоненте.
Технологов интересует не столько распределение концентрации влаги по радиусу  (объему зерна), сколько средняя влажность зерна: именно она входит в материальные балансы, определяет необходимые затраты теплоты на процесс сушки и вообще устанавливается с течением времени в высушенном зерне при его хранении с целью последующего использования. (объему зерна), сколько средняя влажность зерна: именно она входит в материальные балансы, определяет необходимые затраты теплоты на процесс сушки и вообще устанавливается с течением времени в высушенном зерне при его хранении с целью последующего использования.
Усреднение концентраций ведется по канве. В сферическом зерне на текущей радиальной координате  выделяется (см. рис. 11.46) сферический слой бесконечно малой толщины выделяется (см. рис. 11.46) сферический слой бесконечно малой толщины  . Количество влаги в этом шаровом слое объемом . Количество влаги в этом шаровом слое объемом  равно равно  , а в зерне в целом — интегралу от этой величины по объему зерна. С другой стороны, полное количество влаги в зерне выражается как произведение средней ее концентрации , а в зерне в целом — интегралу от этой величины по объему зерна. С другой стороны, полное количество влаги в зерне выражается как произведение средней ее концентрации  на объем зерна на объем зерна  . Приравнивая количества влаги в зерне, записанные различным образом, получаем: . Приравнивая количества влаги в зерне, записанные различным образом, получаем:
 и и  (11.42) (11.42)
При этом средняя концентрация  получается как функция времени; зависимость от получается как функция времени; зависимость от  утрачивается при интегрировании по параметру утрачивается при интегрировании по параметру  и подстановке пределов. и подстановке пределов.
Усреднение концентрации влаги в зерне удобно проводить в безразмерных переменных, отыскивая не  , а комплекс , а комплекс  Это правомерно, поскольку Это правомерно, поскольку  и и  однозначно и линейно связаны между собой. Таким образом, в манере (11.42) имеем: однозначно и линейно связаны между собой. Таким образом, в манере (11.42) имеем:
 (11.42а) (11.42а)
Для выполнения операции интегрирования надо под интеграл в (11.42а) подставить значение  по (11.41): по (11.41):
 (ж) (ж)
Входящий в (ж) интеграл берется по частям. Обозначим  где где  тогдп тогдп  В целом: В целом:
 (з) (з)
поскольку  при при  - целом - целом  а последнее слагаемое в фигурных скобках содержит множитель нуль. а последнее слагаемое в фигурных скобках содержит множитель нуль.
Подставим значение интеграла (з) в выражение (ж), внеся знак «минус» в  получим в нём множитель получим в нём множитель  В целом: В целом:
 (и) (и)
При  чётном чётном  и и  так что фрагмент так что фрагмент  При При  нечётном нечётном  и и  так что указанный фрагмент тоже равен 1. Поэтому окончательно так что указанный фрагмент тоже равен 1. Поэтому окончательно
 (11.43) (11.43)
Для наглядности выпишем несколько первых членов разложения (11.43):
 (к) (к)
Этот ряд при не очень малых значениях  быстро сходится, так как при увеличении номера члена ряда показатель степени быстро растет. Например, при быстро сходится, так как при увеличении номера члена ряда показатель степени быстро растет. Например, при  второе слагаемое составляет от первого лишь 1,3 %, а сумма всех последующих не превышает 0,005 %. Поэтому при второе слагаемое составляет от первого лишь 1,3 %, а сумма всех последующих не превышает 0,005 %. Поэтому при  для технических расчетов вполне можно ограничиться первым членом разложения, т.е. вместо (11.43) записать: для технических расчетов вполне можно ограничиться первым членом разложения, т.е. вместо (11.43) записать:
 (11.43а) (11.43а)
При меньших значениях  второй и последующие члены ряда (11.43), (к) становятся соизмеримыми с первым, и для расчета приходится брать больше слагаемых: их число при определенном значении второй и последующие члены ряда (11.43), (к) становятся соизмеримыми с первым, и для расчета приходится брать больше слагаемых: их число при определенном значении  зависит от требуемой точности расчета. Значения зависит от требуемой точности расчета. Значения  в зависимости от в зависимости от  (или от (или от  )табулированы в специальной литературе. )табулированы в специальной литературе.
Псевдоожиженным слой. Разные зерна в непрерывно работающем ПС (т.е. с постоянным вводом и выводом твердого материала) имеют различное время пребывания в зоне сушки; поэтому и значения средней влажности  для них будут разными. Чтобы определить получающуюся усредненную влажность зерен на выходе из псевдоожиженного слоя для них будут разными. Чтобы определить получающуюся усредненную влажность зерен на выходе из псевдоожиженного слоя  , необходимо учесть их распределение по времени пребывания — соответственно выражению: , необходимо учесть их распределение по времени пребывания — соответственно выражению:

и  (л) (л)
Поскольку перемешивание зерен (частиц) в ПС чрезвычайно интенсивное, то в качестве плотности распределения используется формула для систем идеального перемешивания:  здесь среднее время пребывания зёрен в зоне сушки здесь среднее время пребывания зёрен в зоне сушки  (смысл (смысл  и и 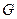 ясен из рис. 11.41). Подставив во второе из выражений (л) значение ясен из рис. 11.41). Подставив во второе из выражений (л) значение  по (11.43), имеем: по (11.43), имеем:
 (м) (м)
Возьмем интеграл  , содержащийся в (м), раскрыв запись , содержащийся в (м), раскрыв запись  и изменив знак (и пределы интегрирования) в ходе преобразований: и изменив знак (и пределы интегрирования) в ходе преобразований:
 (н) (н)
Подставив теперь значение  в (м) и внеся множитель в (м) и внеся множитель 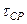 в знаменатель, получим: в знаменатель, получим:
 (о) (о)
Обозначим  и будем трактовать этот комплекс как усредненный диффузионный критерий Фурье (Фика), базирующийся на среднем времени пребывания зерен в рабочей зоне ( и будем трактовать этот комплекс как усредненный диффузионный критерий Фурье (Фика), базирующийся на среднем времени пребывания зерен в рабочей зоне (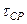 ). Тогда окончательно: ). Тогда окончательно:
 (11.44) (11.44)
Это решение представляет собой медленно сходящийся ряд (даже при высоких значениях  ): в самых благоприятных условиях второе слагаемое составляет более 6% от первого, а третье — более 1,2 %. Здесь даже для техническихрасчетов приходится брать несколько членов ряда (их число определяется необходимой точностью расчетов). ): в самых благоприятных условиях второе слагаемое составляет более 6% от первого, а третье — более 1,2 %. Здесь даже для техническихрасчетов приходится брать несколько членов ряда (их число определяется необходимой точностью расчетов).
Формула (11.44) позволяет решать задачи эксплуатации и проектирования.
В задаче эксплуатации известны массовая производительность по высушиваемому материалу 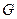 и масса материала в слое и масса материала в слое  . Это позволяет рассчитать . Это позволяет рассчитать  и найти величину и найти величину  . Далее по (11.44) определяют значение концентрационного комплекса . Далее по (11.44) определяют значение концентрационного комплекса  и для известных и для известных  и и 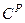 — искомую концентрацию — искомую концентрацию  . Затем по материальному балансу (11.30) при известных . Затем по материальному балансу (11.30) при известных 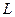 и и  рассчитывают выходное влагосодержание рассчитывают выходное влагосодержание  . Трудный момент здесь — в неопределенности величины . Трудный момент здесь — в неопределенности величины 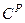 , поскольку в начале расчета неизвестно , поскольку в начале расчета неизвестно  (концентрацию (концентрацию 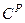 обычно без существенной погрешности можно считать равновесной с обычно без существенной погрешности можно считать равновесной с  ). Это затруднение разрешается путем применения итерационной процедуры — до приемлемой сходимости равновесных величин ). Это затруднение разрешается путем применения итерационной процедуры — до приемлемой сходимости равновесных величин 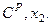
В задачах проектирования заданы значения 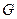 , ,  (или (или 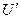 ) и ) и  (или (или 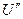 ); неизвестна масса твердого материала ); неизвестна масса твердого материала  в ПС, обеспечивающая получение заданного значения в ПС, обеспечивающая получение заданного значения  . Сначала определяют концентрационный комплекс . Сначала определяют концентрационный комплекс  , причем сложностей с концентрацией , причем сложностей с концентрацией 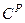 нет, так как нет, так как  (при известном потоке (при известном потоке 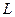 ) отыскивается из материального баланса (11.30). Далее по (11.44) находят ) отыскивается из материального баланса (11.30). Далее по (11.44) находят  . Здесь возможны чисто технические затруднения, так как . Здесь возможны чисто технические затруднения, так как  входит в несколько слагаемых в правой части. Эти затруднения разрешаются использованием ЭВМ или предварительным табулированием функции (11.44): входит в несколько слагаемых в правой части. Эти затруднения разрешаются использованием ЭВМ или предварительным табулированием функции (11.44):  . По найденному . По найденному  рассчитывают рассчитывают  и при известной производительности и при известной производительности 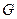 вычисляют искомое вычисляют искомое  . При меньших значениях . При меньших значениях  не удастся получить высушенный материал с обусловленной выходной влажностью не удастся получить высушенный материал с обусловленной выходной влажностью  (или (или 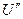 ) — влажность будет выше. ) — влажность будет выше.
На практике удобно оперировать не массой  , а необходимой высотой псевдоожиженного слоя , а необходимой высотой псевдоожиженного слоя 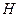 . Ее определяют на основе очевидного соотношения: . Ее определяют на основе очевидного соотношения:
 (п) (п)
в качестве конечного результата принимают высоту ПС не менее рассчитанной по (п): при меньших 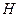 глубина сушки будет недостаточной. глубина сушки будет недостаточной.
Подход к определению сечения аппарата  изложен в разд. 11.8.2. изложен в разд. 11.8.2.
Контрольные вопросы
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




