|
|
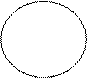
Анализ простых категорических силлогизмов с помощью круговых схемПравильность силлогизма можно легко проверить без знания фигур, модусов и даже общих правил простого категорического силлогизма, опираясь только на иллюстрацию отношения понятий кругами Эйлера. Это называется методом круговых схем для отбора правильных силлогизмов. Логическим основанием данного метода является следующая закономерность: если силлогизм построен правильно, то на схеме отношений понятий-терминов (Р, М, S) данного силлогизма их взаимное расположение, заданное суждениями-посылками, будет абсолютно однозначно определять отношение объёмов понятий субъекта и предиката заключения. Все 19 модусов простого категорического силлогизма в конечном счёте сводимы к четырём правильным модусам первой фигуры, дающим четыре возможных вида выводов: общеутвердительный (А), общеотрицательный (Е), частноутвердительный (I) и частноотрицательный (О). Значит, и схем расположения терминов в правильном силлогизме возможно только четыре. Они представлены на следующих рисунках: Вывод А
Все М есть Р
Все S есть Р
Все люди смертны Сократ - человек
 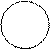 2. Вывод Е 2. Вывод Е
Ни одно S не есть Р
Ни одно дерево не летает Все берёзы - деревья
 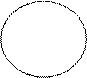 3. Вывод I 3. Вывод I
Все М есть Р
Некоторые S есть Р
Все зебры - полосатые Некоторые лошади - зебры
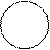
4.
Некоторые S не есть Р
Ни одно растение не говорит Некоторые формы жизни -растения
Примеры ошибок: а) Все студенты сдают экзамены, а некоторые водители не сдают экзаменов. Значит, некоторые водители - не студенты. Все Р есть М
б) Некоторые студенты занимаются музыкой, а ни один попугай музыкой не занимается, следовательно некоторые попугаи не являются студентами.
Некоторые Р есть М Ни одно S не есть М
В обоих примерах вывод с необходимостью не следует из посылок, поскольку отношение субъекта и предиката в заключении не однозначно.
§ 5. Умозаключения, содержащие сложные суждения (Выводы логики высказываний) В этих умозаключениях суждения не расчленяются на субъект и предикат, а рассматриваются как простые суждения, из которых с помощью логических союзов образуются сложные суждения. Выводы, таким образом, делаются не на основе отношения понятий (терминов), а на основе правил отношений суждений. Условные умозаключения Чисто условный силлогизм - умозаключение, в котором обе посылки являются условными суждениями.
Пример: Если сложить 2 нечётных числа, то их сумма будет чётным числом; если их сумма - чётное число, то она будет делиться пополам без остатка. Значит, если сложить 2 нечётных числа, то их сумма будет делиться пополам без остатка. Это отношение суждений выражается формулой: следствие следствия есть следствие основания. Условно-категорический силлогизм - умозаключение, в котором одна посылка - условное суждение, а другая посылка и вывод - категорические суждения. Этот силлогизм имеет два правильных модуса: утверждающий и отрицающий. 1. Утверждающий модус (modus ponens) выражается формулой:
Если во второй посылке утверждается следствие первой посылки, то вывод может быть только вероятным.
2. Отрицательный модус (modus tollens):
Если отрицается основание условной посылки, то вывод может быть только вероятным.
Разделительный силлогизм Чисто разделительный силлогизм состоит только из разделительных посылок, и вывод - тоже разделительное суждение.
По сути, такое умозаключение даёт увеличение количества альтернатив, углубляет дизъюнкцию. В рассуждениях гораздо большее значение имеет разделительно-категорический силлогизм, в котором одна посылка - разделительное суждение, а другая - простое категорическое суждение. Разделительно-категорический силлогизм имеет два правильных модуса. 1. Утверждающе-отрицающий модус (modus ponendo tollens): Разделительная посылка - дизъюнкция альтернатив. Категорическая посылка - утверждение одной из альтернатив. Заключение - категорическое суждение, отрицающее другую (другие) альтернативу.
Необходимым условием правильности вывода по этому модусу является строгость дизъюнкции альтернатив (соединение их союзом "либо"). В случае нестрогой дизъюнкции ("или") вывод с необходимостью не следует.
2. Отрицающе-утверждающий модус (modus tollendo ponens):
В этом модусе правильный вывод возможен при строгой и при нестрогой дизъюнкции разделительной посылки. Необходимым условием правильности вывода по этому модусу является перечисление в разделительной посылке всех возможных альтернатив.
В данном примере не учтена возможность, например, несчастного случая.
  Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам...  Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...  Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор...  Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|