|
|
ПРИНЦИП ИДЕНТИЧНОСТИ И ДЕКОМПОЗИЦИИСтр 1 из 2Следующая ⇒ Глава 3 МЕТОД АНАЛИЗА ИЕРАРХИЙ ВВЕДЕНИЕ
Метод анализа иерархий является систематической процедурой для иерархического представления элементов, определяющих суть любой проблемы. Метод состоит в декомпозиции проблемы на все более простые составляющие части и дальнейшей обработке последовательности суждений лица, принимающего решение (ЛПР), по парным сравнениям. В результате может быть выражена относительная степень (интенсивность) взаимодействия элементов в иерархии. Эти суждения затем выражаются численно. Метод анализа иерархии включает процедуры синтеза множественных суждений, получения приоритетности критериев и нахождения альтернативных решений. Полезно отметить что полученные таким образом значения являются оценками в шкале отношений и соответствуют так называемым жестким оценкам. Решение проблемы есть процесс поэтапного установления приоритетов. На первом этапе выявляются наиболее важные элементы проблемы, на втором — наилучший способ проверки наблюдений испытания и оценка элементов; следующим этапом может быть выработка способа применения решения и оценка его качества. Весь процесс подвергается проверке и переосмысливанию до тех пор, пока не будет уверенности, что процесс охватил все важные характеристики, необходимые для представления и решения проблемы. Процесс может быть проведен над последовательностью иерархий: в этом случае результаты, полученные в одной из них, используются в качестве входных данных при изучении следующей. Предложенный метод систематизирует процесс решения такой многоступенчатой задачи. Наконец, если допустить, что интуиция и субъективные оценки являются основным исходным материалом, на основании которого индивидуум получает ясное представление о своих творческих возможностях, то суждение о превосходстве одного элемента над другим и интенсивность этих суждений можно использовать для выражения внутренних чувств и склонностей. Суждения расширяют рамки общения, укрупняя кластеры и элементы, имеющиеся в иерархии по определенной проблеме. Такой подход к решению проблемы выбора исходит из естественной способности людей думать логически и творчески, определять события и устанавливать отношения между ними. Отметим, что человеку присущи два характерных признака аналитического мышления: один — умение наблюдать и анализировать наблюдения; другой — способность устанавливать отношения между наблюдениями, оценивая уровень взаимосвязей между отношениями, а затем синтезировать эти отношения в общее восприятие наблюдаемого. Вышеперечисленное дает представление о принципе идентичности и декомпозиции, принципах дискриминации, сравнительного суждения и синтезирования. В этой главе кратко изложен МАИ и на примерах проиллюстрировано его использование. Кроме того, рассмотрены вопросы согласованности иерархий и зависимости между ее элементами. Детально метод анализа иерархий описан в [12], а его приложения в различных реальных системах проиллюстрированы в [13].
ПРИНЦИП ДИСКРИМИНАЦИИ И СРАВНИТЕЛЬНЫХ СУЖДЕНИЙ После иерархического или сетевого воспроизведения проблемы, возникает вопрос: как установить приоритеты критериев и оценить каждую из альтернатив по критериям, выявив самую важную из них?
А. ПАРНЫЕ СРАВНЕНИЯ В МАИ элементы задачи сравниваются попарно по отношению к их воздействию («весу», или «интенсивности») на общую для них характеристику. Проведем парные сравнения, приводящие к матричной форме — квадратной таблице, в которой числа могут быть расположены следующим образом:
Скобки, в которые заключена матрица размерностью 4×4 используются для обозначения стандартной формы матрицы. Сравнивая набор составляющих проблемы друг с другом, получаем следующую квадратную матрицу:
Очевидно, что эта матрица имеет свойства обратной симметричности, т. е.
где индексы i и j относятся к строке и столбцу соответственно. Позже будет объяснена важность появления обратных чисел. Квадратная матрица имеет равное число строк и столбцов, а также другие полезные характеристики, такие, как собственные векторы и собственные значения. Об этих понятиях мы будем говорить в дальнейшем, когда попытаемся «решить» квадратную обратносимметричную матрицу. Смысл таких вычислений заключается в том, что они определяют способ количественного определения сравнительной важности факторов или результатов в проблемной ситуации. На факторах с наибольшими величинами важности будет сконцентрировано внимание при решении проблемы или разработке плана действия. Важно понять, что парные сравнения элементов производится с использованием субъективных суждений, численно оцениваемых по шкале (которая будет описана позже), а затем решается проблема нахождения компонент w. Когда проблемы представлены иерархически, матрица составляется для сравнения относительной важности критериев на втором уровне по отношению к обшей цели на первом уровне. Подобные матрицы должны быть построены для парных сравнений каждой альтернативы на третьем уровне по отношению к критериям второго уровня. Матрица составляется, если записать сравниваемую цель (или критерий) вверху и перечислить сравниваемые элементы слева и сверху. В примере, связанном с покупкой нового дома, потребуется 5 таких матриц, одна для второго уровня иерархии и четыре для третьего уровня. Эти матрицы представлены в табл. 3.1 и 3.2.
Таблица 3.1 - Покупка дома: матрица попарных сравнений для уровня 2
Отметим, что клетки этих матриц не заполнены; они оставлены для оценок или суждений об относительной важности сравниваемых отдельных предметов по отношению к цели, или критерию, обозначенному вверху. Если существует шкала сравнений, т. е. имеется некоторый способ измерения, то данные могут использоваться для проведения сравнений; иначе клетки заполняются оценками, полученными в результате субъективных, но продуманных суждений индивидуума или группы, решающей проблему. Шкала для измерения таких суждении будет приведена далее.
Таблица 3.2 - Покупка дома: матрицы попарных сравнений дли уровня 3
Г. КАКИЕ ЗАДАВАТЬ ВОПРОСЫ ПРИ ПРОВЕДЕНИИ СРАВНЕНИЙ? Наш опыт показал, что при проведении попарных сравнений в основном ставятся следующие вопросы. При сравнении элементов А и Б: - какой из них важнее или имеет большее воздействие? - какой из них более вероятен? - какой из них предпочтительнее? Для большинства различных приложений, которые мы провели, все задаваемые вопросы попадали в одну из этих трех категорий. При сравнении критериев обычно спрашивают, какой из критериев более важен; при сравнении альтернатив по отношению к критерию — какая из альтернатив более желательна; при сравнении сценариев, получаемых из критерия,— какой из сценариев более вероятен.
СИНТЕЗ ПРИОРИТЕТОВ На этом этапе в нашем примере семья построила иерархию, составила матрицы и выразила субъективные парные суждения. Однако что все эти цифры означают и как они помогут определить тот дом, который следует купить? В этом разделе описывается, каким образом сочетаются иерархическая декомпозиция и шкалам относительной важности для получения осмысленных подходов км многокритериальным проблемам планирования.
В. ПРИНЦИП СИНТЕЗА Теперь обратимся к принципу синтеза. Приоритеты синтезируются, начиная со второго уровня вниз. Локальные приоритеты перемножаются на приоритет соответствующего критерия на вышестоящем уровне исуммируются по каждому элементу в соответствии критериями на которые воздействует этот элемент. (Каждый элемент второго уровня умножается на единицу, т. е. на вес единственной цели самого верхнего уровня.) Это дает составной, или глобальный, приоритет того элемента, который затем используется для взвешивания локальных приоритетов элементов, сравниваемых поотношению к нему как к критерию и расположенных уровнем ниже. Процедура продолжается до самого нижнего уровня.
Глава 3 МЕТОД АНАЛИЗА ИЕРАРХИЙ ВВЕДЕНИЕ
Метод анализа иерархий является систематической процедурой для иерархического представления элементов, определяющих суть любой проблемы. Метод состоит в декомпозиции проблемы на все более простые составляющие части и дальнейшей обработке последовательности суждений лица, принимающего решение (ЛПР), по парным сравнениям. В результате может быть выражена относительная степень (интенсивность) взаимодействия элементов в иерархии. Эти суждения затем выражаются численно. Метод анализа иерархии включает процедуры синтеза множественных суждений, получения приоритетности критериев и нахождения альтернативных решений. Полезно отметить что полученные таким образом значения являются оценками в шкале отношений и соответствуют так называемым жестким оценкам. Решение проблемы есть процесс поэтапного установления приоритетов. На первом этапе выявляются наиболее важные элементы проблемы, на втором — наилучший способ проверки наблюдений испытания и оценка элементов; следующим этапом может быть выработка способа применения решения и оценка его качества. Весь процесс подвергается проверке и переосмысливанию до тех пор, пока не будет уверенности, что процесс охватил все важные характеристики, необходимые для представления и решения проблемы. Процесс может быть проведен над последовательностью иерархий: в этом случае результаты, полученные в одной из них, используются в качестве входных данных при изучении следующей. Предложенный метод систематизирует процесс решения такой многоступенчатой задачи. Наконец, если допустить, что интуиция и субъективные оценки являются основным исходным материалом, на основании которого индивидуум получает ясное представление о своих творческих возможностях, то суждение о превосходстве одного элемента над другим и интенсивность этих суждений можно использовать для выражения внутренних чувств и склонностей. Суждения расширяют рамки общения, укрупняя кластеры и элементы, имеющиеся в иерархии по определенной проблеме. Такой подход к решению проблемы выбора исходит из естественной способности людей думать логически и творчески, определять события и устанавливать отношения между ними. Отметим, что человеку присущи два характерных признака аналитического мышления: один — умение наблюдать и анализировать наблюдения; другой — способность устанавливать отношения между наблюдениями, оценивая уровень взаимосвязей между отношениями, а затем синтезировать эти отношения в общее восприятие наблюдаемого. Вышеперечисленное дает представление о принципе идентичности и декомпозиции, принципах дискриминации, сравнительного суждения и синтезирования. В этой главе кратко изложен МАИ и на примерах проиллюстрировано его использование. Кроме того, рассмотрены вопросы согласованности иерархий и зависимости между ее элементами. Детально метод анализа иерархий описан в [12], а его приложения в различных реальных системах проиллюстрированы в [13].
ПРИНЦИП ИДЕНТИЧНОСТИ И ДЕКОМПОЗИЦИИ
Принцип идентичности и декомпозиции предусматривает структурирование проблем в виде иерархии или сети, что является первым этапом применения МАИ. В наиболее элементарном виде иерархия строится с вершины (целей — с точки зрения управления) через промежуточные уровни (критерии, от которых зависят последующие уровни) к самому низкому уровню (который обычно является перечнем альтернатив). Существует несколько видов иерархий. Самые простые — доминантные иерархии, которые похожи на перевернутое дерево с основой в вершине. Холлархии — это по существу доминантные иерархии с обратной связью. Китайский ящик (или модулярные иерархии) растет в размерах от простейших элементов или компонент (внутренние ящики) ко все более крупным совокупностям (внешние ящики). В биологии интерес представляют неогенетические иерархии, в которых новые верхние уровни возникают последовательно в течение эволюции. Мы сконцентрируем внимание на доминантных иерархиях, хотя теория, описанная ниже, распространяется и на другие иерархические формы. Иерархия считается полной, если каждый элемент заданного уровня функционирует как критерий для всех элементов нижестоящего уровня (см. рис. 3.1). В противном случае иерархия — неполная. Нетрудно понять процесс определения весов в случае неполной иерархии, так как используются приоритеты соответствующего элемента, по отношению к которому производится оценка, т. е. иерархия может быть разделена на подиерархии, имеющие общий самый верхний элемент. Простой пример, который используется в большей части этой главы для объяснения МАИ, наилучшим образом иллюстрирует иерархическое представление задачи. Далее рассматриваются более сложные примеры, иллюстрирующие спектр приложений, в которых может быть применен МАИ. Семья среднего достатка решила купить дом. В результате обсуждения удалось определить восемь критериев, которым, как казалось, должен удовлетворять дом. Эти критерии можно разбить на три кластера: экономический, географический и физический. Хотя можно было начать с исследования сравнительной важности кластеров, члены семьи чувствовали, что им хочется определять сравнительную важность всех факторов, не имея дела с кластерами. Задача заключалась в выборе одного из трех домов-кандидатов. Первый шаг состоит в декомпозиции и представлении задачи в иерархической форме. На первом (высшем) уровне находится общая печь — «Дом». На втором уровне находятся четарефактора или критериев, уточняющих цель, и на третьем (нижнем) уровне находятся три дома-кандидата, которые должны быть оценены по отношению к критериям второго уровня. Далее следует определение критериев и графическое представление иерархии. У членов семьи были следующие критерии:
    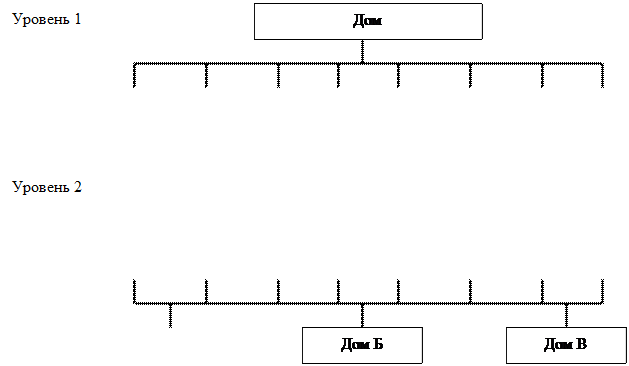
Рис. 3.1. Декомпозиция задачи в иерархию 1. Размеры дома: емкость хранилищ; размеры комнат; число комнат; общая площадь дома. 2. Окрестности: интенсивность движения транспорта; безопасность; хороший вид; низкие налоги; ухоженные окрестности. 3. Когда построен дом: не нуждается в объяснении. 4. Финансовые условия: допускаемая закладная, условия продажи и банковский кредит. Такая форма нисходящей декомпозиции может быть легко использована для задач широкого класса. К тому же несложная модификация с включением петель обратной связи охватит еще более широкий класс задач. Закон иерархической непрерывности требует, чтобы элементы нижнего уровня иерархии были сравнимы попарно по отношению к элементам следующего уровня и т. д. вплоть до вершины иерархии. Например, надо получить имеющие смысл ответы на вопросы такого типа: «Насколько дом А лучше дома Б или В по критерию окрестности?» или «Насколько по отношению к основной цели размеры дома важнее расположения к автобусным маршрутам?» и т. д. Когда есть сомнения относительно того, какие уровни ввести в иерархию, закон иерархической непрерывности обеспечивает связь. Целью построений является получение приоритетов элементов на последнем уровне, наилучшим образом отражающих относительное воздействие на вершину иерархии. Важно отметить, что МАИ требует структурирования проблемы участниками в процессе решения; в этом простом примере члены семьи составляют иерархию в соответствии с их потребностями, пониманием ограничений (например, денежных средств) и существующими вариантами выбора. Этот этап требует обсуждения, чтобы быть уверенными, что критерии и альтернативы отражают весь диапазон предпочтений и восприятия участников. Необязательно, чтобы все участники в процессе планирования пришли к согласию по всем компонентам проблемы. Участники процесса позже смогут выразить свои предпочтения относительно критериев и альтернатив. Поэтому аргументы, которые они приводят для обоснования своих предпочтений, могут «утонуть или всплыть». Иначе говоря, не нужно чувствовать стесненности при начальном иерархическом описании задачи. Тем не менее решающим является согласие участников процесса планирования по высшему уровню иерархии — цели, или вершине проблемы, поскольку это предопределит характер их последующих суждений. Определение цели может потребовать длительных предварительных рассуждений и переговоров. Например, члены семьи первоначально пришли к заключению, что их система нуждается в фундаментальном изменении (покупка другого дома вместо модификации старого), что включает оценку потребностей семьи, прогноз о росте семьи, прогноз изменения характеристик окружающей среды и конъюнктуры, например увеличивающейся коммерциализации, которая может снизить цену их дома.   Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор...  Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...  Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем...  Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|