|
|
Лазерный однокомпонентный измеритель вибрацииСтр 1 из 3Следующая ⇒ Введение Уникальные физические особенности лазерных методов определяют многие их достоинства. Это возможность дистанционного бесконтактного измерения вибрации и отсутствие влияния на резонансные свойства объектов, в том числе микроскопических размеров; возможность измерений без предварительной подготовки поверхности объекта и оперативное измерение вибраций в различных точках объекта в опасной для персонала зоне (химически агрессивной, с высокой температурой, радиацией и т.д.). Лазерный однокомпонентный измеритель вибрации относится к измерительной технике и может быть использован для измерения параметров вибрации диффузно рассеивающих объектов. Цель изобретения – повышение точности измерений за счет повышения отношения сигнал/шум. В данной работе будет рассмотрено назначение, состав и работа лазерного однокомпонентного измерителя вибрации, а также формула его изобретения. Следующий этап курсовой работы - расчет по методу Мюллера прохождения неполяризованного лазерного пучка через преобразователь поляризации и расчет по методу Джонса прохождения полностью поляризованного лазерного пучка через оптическое устройство; сравнив оба метода расчета, сформулировать выводы. Метод Мюллера используется, как правило, для описания оптических схем некогерентной оптики. Этот метод позволяет описывать прохождение лазерных пучков, либо световых пучков не когерентных для случаев, когда эти пучки полностью поляризованы, частично поляризованы или неполяризованы. Метод Джонса – описывает прохождение лазерного пучка через когерентный оптический преобразователь, для случая, когда лазерные пучки полностью когерентны и полностью поляризованы (степень поляризации 100%). Этот метод учитывает фазовые соотношения и соответствующие преобразования в фазы.
Лазерный однокомпонентный измеритель вибрации Формула изобретения 1. Лазерный однокомпонентный измеритель вибрации, содержащий оптически связанные первый оптический квантовый генератор, оптический преобразователь, диафрагму и фокусирующий объектив, первый и второй светоделители, делящие лучи на два пучка, первое, второе и третье зеркала, первый и второй собирающие объективы, первый интеренференционный светофильтр на длину волны λ1, первый интеренференционный светофильтр на длину волны λ2, фотоприемник и блок обработки, вход которого связан с выходом фотоприемника, отличающийся тем, что, с целью повышения точности измерений, он снабжен вторым оптическим квантовым генератором, вращателем плоскости поляризации, расположенным между вторым оптическим квантовым генератором и оптическим преобразователем, третьим светоделителем, делящим луч на два пучка, первым и вторым фазорегуляторами, первым интерференционным светофильтром на длину волны λ3, вторым интерференционным светофильтром на длину волны λ1, вторым интерференционным светофильтром на длину волны λ2, вторым интерференционным светофильтром на длину волны λ3 и световодом, первый и второй оптические квантовые генераторы выполнены с возможностью излучения на трех длинах волн
2. Пространственное моделирование рассеянного когерентного излучения на сферических микрочастицах.
Формирование зон измерения:
Рис. 2.1 Ход лучей в дифференциальной схеме: ОКГ – оптический квантовый резонатор; 1 – пучок излучения; 2, 3 – пучки на выходе расщепителя; 4 – расщепитель пучка; α – угол, под которым пересекаются два пучка; 6 – объектив; f – фокусное расстояние объектива, центр зона измерения.
При формировании зоны измерения при помощи двух когерентных пучков 2 и 3 (рис.2.1.) в зоне пересечения этих пучков образуется интерференционная область, в которой интерференционные максимумы перпендикулярны плоскости пучков и параллельны оптической оси схемы. Пусть
а) 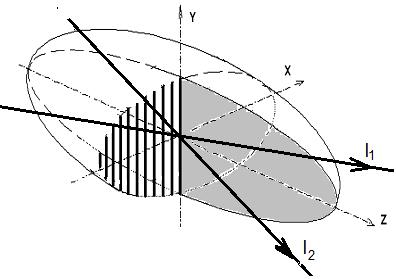
б) в)
г) д) Рисунок 2.2 а) Формування зони вимірювання; б) фотографія гармонічної зміни освітленості у площині OXfYf, коли ступень просторової когерентності
Период интерференционной картины:
Интенсивность перераспределения:
где
где
При равенстве интенсивностей двух формирующих пучков I2 = I3, распределение интенсивностей в интерференционной картине:
Сигнал в максимуме получается в 4-е раза больше интенсивности излучения пучка:
Амплитуда распределения интенсивности излучения носит волновой характер. Наибольшее значение интенсивности в интерференционной картине происходит при:
Максимум имеет место в случае, когда n=1,2,3… - в этом случае отмечаются максимумы интерференционной картины:
Минимальное значение интенсивности в интерференционной картине получается, когда:
в этом случае отмечаются минимумы интерференционной картины:
При пересечении двух пучков в зоне измерения образуется интерференционная картина (интерференционное поле) рис.2.3.
Рис. 2.3 Формирование зоны измерения.
Распределение интенсивности в лазерном пучке представляет собой распределение Гаусса – в центре пучка максимум. Размеры эллипсоида определяются из соотношений:
где
Рис. 2.4.Размеры эллипсоида (зоны измерения)
Рис. 2.6. Условие получения градуировочной характеристики. α - угол между лазерными пучками; S – расстояние между пучками в плоскости приёма (расчета).
Дифракция Фраунгофера .
Выделяемая площадь расчета
Рис. 3.9
Рис. 2.7. Выделяемая площадь расчета Дифракция рассматривает процессы отклонения направления распространения света от прямолинейного при встрече с некоторыми препятствиями или при отражении от них. В случае дифракции Фраунгофера рассматривается падение на препятствие плоской волны (бесконечно удаленный источник света) и подразумевается, что зона наблюдения удалена от препятствия на достаточно большое расстояние (находится на бесконечности). Коротко говоря, это “дифракция в параллельных лучах”. Расчитываем интенсивность распределения в области ограниченной прямоугольником (пространственным фильтром) (рис. 2.8.).
Рис. 2.8. Пространственное дифракционное распределение
Пусть в начале системы координат Ox1y1z1 находится сферическая непрозрачная частица с диаметром D на много большим длины волны облучающих пучков. Если представить электрическое поле облучающих пучков в зоне измерения в единой системе координат и предположить, что угол между пучками α мал, то результирующее дифрагированное поле, наблюдаемое вблизи оптической оси схемы в плоскости Ох0y0 , расположенное от зоны измерения на расстоянии R>>D, то можно определить на основе дифракционной теории в приближении Фраунгофера: I(x) = где Функции Бесселя, обозначаемые символом Jv(x), представляют собой решения линейного дифференциального уравнения второго порядка, в которое входит один произвольный параметр v:
Параметр v называется индексом или порядком функции Бесселя Jv (x) и он может принимать как вещественные, так и комплексные значения. Функции Бесселя обычно возникают как решения для волнового уравнения, подчиненного цилиндрическим граничным условиям. Координаты зоны измерения - Диапазон значений координаты х частицы в зоне измерения:
- Интенсивность в зоне измерения:
Построим синфазные сигналы на выходе фотоприемников (рис.2.13 – 2.15.):
Рис. 2.13. Амплитуда сигнала на выходе 1-го фотоприемника
Рис. 2.14. Амплитуда сигнала на выходе 2-го фотоприемника
Рис. 2.15. Разность интенсивностей 1-го и 2-го пучков Метод Мюллера и Джонса Расчетные методы Мюллера и Джонса чрезвычайно полезны для определения влияния различных поляризаторов и фазовых пластинок на проходящий через них пучок света. Метод Мюллера применим также к рассеянию света. Метод Мюллера представляет собой матричное описание светового пучка и оптического устройства, через которое проходит свет, и позволяет вычислить результат взаимодействия света с этим устройством. Преимущества метода Мюллера состоят в том, что он дает возможность: а) сконцентрировать все необходимые для описания пучка света параметры в едином выражении, б) записать в едином выражении все параметры поляризатора или фазовой пластинки и в) получить результат взаимодействия света с системой различных оптических элементов (поляризаторы, фазовые пластинки, рассеивающие устройства) рассеивающие устройства) путем простого перемножения соответствующих выражений по определенным правилам. Пучок света описывается вектором Стокса, определяемым четырьмя параметрами I, М, С, S, которые связаны с интенсивностью, преимущественной горизонтальной поляризацией, преимущественной поляризацией под углом +45° и преимущественной правой круговой поляризацией. Этот вектор записывается обычно в виде вертикального столбца или (менее формально) в виде горизонтальной строки:
Спектральная ширина пучка предполагается, с одной стороны, достаточно большой для того, чтобы свет мог быть неполяризованным, а с другой стороны — достаточно малой, чтобы применяемые оптические устройства можно было считать ахроматическими. Выражение, описывающее любое оптическое устройство (поляризатор, фазовую пластинку и т. д.), называется матрицей Мюллера. Она состоит из четырех строк и четырех столбцов 4 Матрица описывает оптическое устройство по отношению только к одному выходящему пучку света. Так, с помощью матрицы Мюллера можно исследовать только один из двух пучков, выходящих из призмы Волластона. Если же оба они представляют интерес, то необходимо пользоваться двумя матрицами и провести два отдельных расчета. Умножение матриц Мюллера производится по обычным правилам матричной алгебры. Необходимо соблюдать следующее условие: вектор, представляющий падающий свет, записывается справа, а матрицы, соответствующие различным устройствам, располагаются последовательно друг за другом, так что матрица устройства, проходимого светом последним, записывается слева. Метод расчета, предложенный в 1940 и 1941 гг. Джонсом, представляет собой другой способ, в котором входящий пучок описывается с помощью вектора, оптическое устройство — с помощью матрицы, а результат взаимодействия также получается умножением вектора на матрицу. Преимущества метода Джонса по сравнению с методом Мюллера состоят в том, что, во-первых, в нем используются матрицы меньшего размера BX2 вместо 4X4) и, вовторых, метод применим для решения таких задач, в ко- торых необходимо учитывать фазовые соотношения. В методе Джонса многие элементы матриц являются комплексными. Однако метод Джонса совершенно неприменим к деполяризующим устройствам. Таким образом, каждый метод имеет свои недостатки и преимущества. При использовании метода Джонса необходимо записать вектор Джонса для входящего света, затем выписать соответствующие матрицы Джонса для поляризаторов и фазовых пластинок, через которые проходит свет, и, перемножая эти выражения, получить вектор Джонса для выходящего света. Вектор Джонса, введенный Джонсом в 1941 г., описывает поляризованный луч с максимальной алгебраической краткостью и чрезвычайно удобен при решении тех задач, в которых важно учитывать фазовые соотношения между пучками. Вектор Джонса представляет собой столбец из двух элементов, который описывает форму поляризации пучка и амплитуду компонент в некоторой точке луча. Если свет распространяется вдоль оси Z, то вектор имеет общую форму:
где Ех и Еу — скалярные компоненты электрического вектора в определенный момент вдоль осей X и У, Ах — максимальная величина Еx а Ау — максимальная величина Е; параметр Вообще говоря, каждый элемент столбца является комплексной величиной. Мы можем привести вектор к следующей эквивалентной форме:
Так как абсолютная величина любого члена вида
Каждая матрица описывает данное устройство при заданной ориентации и для фиксированной входной поверхности. Чтобы определить матрицу Джонса, исходят из обычного математического выражения, описывающего монохроматический (поляризованный) цуг волн и математическим путем определяют те изменения, которые возникают при введении на пути света данного поляризатора или фазовой пластинки. Чтобы найти результат действия последовательности оптических устройств на полностью поляризованный пучок, справа следует записать вектор Джонса входящего пучка, затем справа налево — матрицы проходимых светом устройств, так что матрица самого последнего устройства оказывается расположенной слева. Результат умножения зависит от того, в какой последовательности записаны матрицы.
Рис. 3.2. Оптическое устройство (ОУ) Решение: 1. Определим матрицы Джонса для каждого оптического элемента. Матрица Джонса линейного поляризатора П1: θ1=90
2. Матрица Джонса для четвертьволновой фазовой пластины λ/4: θ2=85 j =
3. Матрица Джонса для линейного поляризатора П2: θ3=55
4. Матрица Джонса для правоциркулярной фазовой 90
5. Матричное уравнение Джонса для прохождения левоциркулярного луча всех элементов ОУ:
В – единичная интенсивность лазерного луча на входе ОУ
6. Вектор Джонса лазерного пучка на выходе ОУ:
7. Матрица Джонса для ОУ:
8. Вектор Джонса лазерного пучка на выходе ОУ:
Литература
1. А. Джерард, Д.М. Бери. Введение в матричную оптику. М. – “Мир”, 1965. – 341с. 2. Ванюрихин А.Н., Герчановская В.П. «Оптико-электронные поляризационные устройства». Издательство "Техника", К., 1989.- 160с. 3. Ватсон Г.Н. Теория бесселевых функций. – М.: ИЛ, 1949. – Т. I. –798с. 4. Землянский В. М. Лазерный однокомпонентный измеритель вибрации. А. с. СССР № 1341498, приоритет от 31.10.1983 5. Интернет: · http://pda.coolreferat.com/ Лазерные измерители вибрации, виброметры · http://en.wikipedia.org/wiki/Spatial_filter · www.physics.org.ua/lectures/3/difr-1.doc 6. Ландсберг Г.С. Оптика. Учебн. пособие: Для вузов. – 6-е узд., стерео. – М.: ФИЗМАТЛИТ, 2003. – 848с. 7. Макаров Е. Г. Mathcad: учебный курс. - Издат.: Питер, 2009. – 384c. 8. Р. Кольер, К. Беркхарт, Л. Лин "Оптическая голография", "Мир", Москва, 1973. – 686c. 9. Сивухин Д. В. Общий курс физики. Том 4. Оптика, 1980. - 768c. 10. У. Шерклифф. «Поляризованный свет»: М. – “Мир”, 1965. – 185с.
Введение Уникальные физические особенности лазерных методов определяют многие их достоинства. Это возможность дистанционного бесконтактного измерения вибрации и отсутствие влияния на резонансные свойства объектов, в том числе микроскопических размеров; возможность измерений без предварительной подготовки поверхности объекта и оперативное измерение вибраций в различных точках объекта в опасной для персонала зоне (химически агрессивной, с высокой температурой, радиацией и т.д.). Лазерный однокомпонентный измеритель вибрации относится к измерительной технике и может быть использован для измерения параметров вибрации диффузно рассеивающих объектов. Цель изобретения – повышение точности измерений за счет повышения отношения сигнал/шум. В данной работе будет рассмотрено назначение, состав и работа лазерного однокомпонентного измерителя вибрации, а также формула его изобретения. Следующий этап курсовой работы - расчет по методу Мюллера прохождения неполяризованного лазерного пучка через преобразователь поляризации и расчет по методу Джонса прохождения полностью поляризованного лазерного пучка через оптическое устройство; сравнив оба метода расчета, сформулировать выводы. Метод Мюллера используется, как правило, для описания оптических схем некогерентной оптики. Этот метод позволяет описывать прохождение лазерных пучков, либо световых пучков не когерентных для случаев, когда эти пучки полностью поляризованы, частично поляризованы или неполяризованы. Метод Джонса – описывает прохождение лазерного пучка через когерентный оптический преобразователь, для случая, когда лазерные пучки полностью когерентны и полностью поляризованы (степень поляризации 100%). Этот метод учитывает фазовые соотношения и соответствующие преобразования в фазы.
Лазерный однокомпонентный измеритель вибрации   Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор...  ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры...  Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? - задался я вопросом...  Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|