Трение по наклонной плоскости
 Рассмотрим различные случаи движения тела по наклонной плоскости с углом наклона Рассмотрим различные случаи движения тела по наклонной плоскости с углом наклона  . .
Случай 1. Тело движется вверх по наклонной плоскости под действием горизонтальной силы 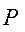 , являющейся движущей силой, и вертикальной силы , являющейся движущей силой, и вертикальной силы  , являющейся силой сопротивления (рис.6.4, а). , являющейся силой сопротивления (рис.6.4, а).
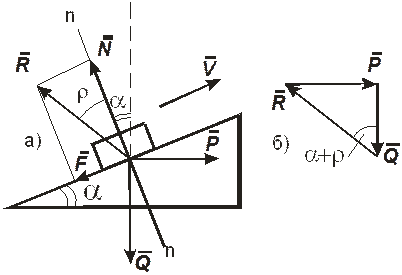
Рис.6.4
Кроме этих сил, на тело будет действовать реакция со стороны наклонной плоскости 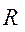 , которая отклонена от нормали , которая отклонена от нормали 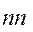 в сторону, противоположную движению на угол трения в сторону, противоположную движению на угол трения 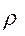 . При равномерном движении сумма сил, действующих на тело, равна нулю: . При равномерном движении сумма сил, действующих на тело, равна нулю:
 . .
На рис 3,б по этому уравнению построен план сил, из которого следует что сила 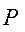 равна равна
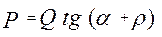 (6.4) (6.4)
Случай 2. Тело движется вниз по наклонной плоскости под действием вертикальной движущей силы  и горизонтальной силы сопротивления и горизонтальной силы сопротивления 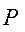 (рис.6.4,а). (рис.6.4,а).

Рис.6.5
При равномерном движении
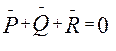
На рис 4,б по этому уравнению построен план сил, из которого следует, что сила 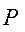 равна равна
. 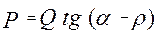 . (6.5) . (6.5)
Из уравнения (5) видно, что если угол  меньше угла трения меньше угла трения 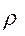 , то сила , то сила
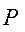 оказывается отрицательной. Это значит, что для возможности движения тела сила оказывается отрицательной. Это значит, что для возможности движения тела сила 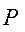 должна быть направлена в противоположную сторону, т. е. должна стать так же, как и сила должна быть направлена в противоположную сторону, т. е. должна стать так же, как и сила  , движущей силой. Такая наклонная плоскость, у которой угол наклона , движущей силой. Такая наклонная плоскость, у которой угол наклона  меньше угла трения меньше угла трения 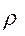 , называется самотормозящей. , называется самотормозящей.
№9
9. Трение скольжения во вращательной кинематической паре
Пусть опорная часть вала – цапфа, вращающаяся в подшипнике скольжения, прижимается к подшипнику силой  (рис. 6.8). Со стороны подшипника на вал в некоторой точке (рис. 6.8). Со стороны подшипника на вал в некоторой точке  при этом будет действовать нормальная реакция при этом будет действовать нормальная реакция  , являющейся равнодействующей всех элементарных сил давлений, распределенных на поверхности соприкосновения цапфы и подшипника. В этой же точке , являющейся равнодействующей всех элементарных сил давлений, распределенных на поверхности соприкосновения цапфы и подшипника. В этой же точке  будет действовать сила трения будет действовать сила трения 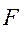 , направленная по касательной к окружности цапфы против вращения. , направленная по касательной к окружности цапфы против вращения.
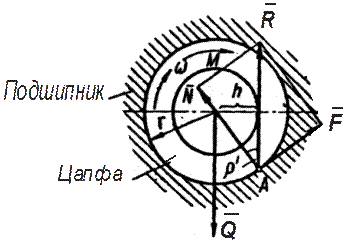
Рис.6.8
Складывая нормальную реакцию  и силу трения и силу трения 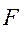 , получим полную реакцию , получим полную реакцию 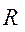 , которая равна по величине, но направлена противоположно силе , которая равна по величине, но направлена противоположно силе  . Реакция . Реакция 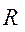 отклонена от нормали на угол трения отклонена от нормали на угол трения 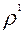 . Этот фиктивный (приведенный) угол трения отличается от действительного . Этот фиктивный (приведенный) угол трения отличается от действительного 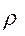 для материалов вала и подшипника и зависит от закона распределения давления. для материалов вала и подшипника и зависит от закона распределения давления.
Фиктивные коэффициенты трения будут равны:
Для не приработавшихся цапф  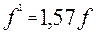 ; ;
Для приработавшихся цапф 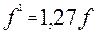 . .
Фиктивный угол трения 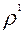 равен равен
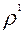 = =  . .
Реакция 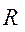 (рис.6.8) создает относительно оси момент сопротивления (момент трения) (рис.6.8) создает относительно оси момент сопротивления (момент трения)
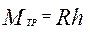 , ,
направленной противоположно движущему моменту 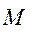 . Величина плеча . Величина плеча  , как видно из рисунка, равна , как видно из рисунка, равна
 = = 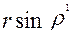 , ,
где 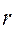 -радиус опорной части вала. -радиус опорной части вала.
Так как угол трения очень мал, то
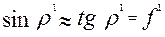 . .
Следовательно
 = =  . (6.9) . (6.9)
Тогда момент сил трения равен
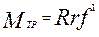 (6.10) (6.10)
Итак, полная реакция 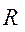 проходит при учете сил трения не через ось вращения вала, а отстоит от нее на расстоянии проходит при учете сил трения не через ось вращения вала, а отстоит от нее на расстоянии  , т.е. является касательной к окружности радиусом , т.е. является касательной к окружности радиусом  . Эта окружность называется кругом трения. . Эта окружность называется кругом трения.
№11
Трение качения
Пусть цилиндр (или шар), на который действует вертикальная нагрузка  , проходящая через ось цилиндра, перекатывается по горизонтальной плоскости (рис.6.9,а). Представим, что цилиндр и плоскость являются абсолютно жесткими. Тогда касание цилиндра и плоскости происходит в точке , проходящая через ось цилиндра, перекатывается по горизонтальной плоскости (рис.6.9,а). Представим, что цилиндр и плоскость являются абсолютно жесткими. Тогда касание цилиндра и плоскости происходит в точке  , и нормальная реакция , и нормальная реакция  проходит также через ось цилиндра. В этом случае нет никакого сопротивления качению. проходит также через ось цилиндра. В этом случае нет никакого сопротивления качению.
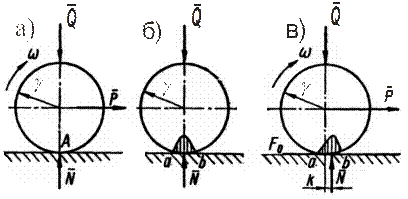
Рис 6.9
В действительности реальные тела всегда подвергаются упругим и пластическим деформациям.
Если цилиндр, на который действует сила  , неподвижно лежит на плоскости, то на некотором участке контакта , неподвижно лежит на плоскости, то на некотором участке контакта  (рис.6.9,б) возникают деформации и напряжения, которые распределяются по некоторому закону. При неподвижном цилиндре кривая распределения напряжений симметрична относительно диаметра. (рис.6.9,б) возникают деформации и напряжения, которые распределяются по некоторому закону. При неподвижном цилиндре кривая распределения напряжений симметрична относительно диаметра.
Если теперь к цилиндру приложить силу 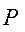 и начать его катить (рис.6.10,в), то впереди цилиндра деформация и напряжения будут возрастать, а сзади - убывать. Вследствие внутреннего трения материалов цилиндра и плоскости кривые нагрузки и разгрузки не совпадают. Поэтому напряжение впереди цилиндра будет больше, чем сзади. В результате этого нормальная реакция и начать его катить (рис.6.10,в), то впереди цилиндра деформация и напряжения будут возрастать, а сзади - убывать. Вследствие внутреннего трения материалов цилиндра и плоскости кривые нагрузки и разгрузки не совпадают. Поэтому напряжение впереди цилиндра будет больше, чем сзади. В результате этого нормальная реакция  будет смещена вперед относительно вертикального диаметра на величину будет смещена вперед относительно вертикального диаметра на величину  .Таким образом, возникает пара сил .Таким образом, возникает пара сил  и и  , создающая моме6т сопротивления качению , создающая моме6т сопротивления качению 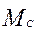 , равный , равный
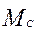 = = 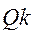 . (6.11) . (6.11)
Движущий момент 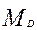 , создаваемый парой сил , создаваемый парой сил 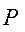 и и 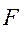
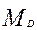 = =  . (6.12) . (6.12)
Для равномерного качения необходимо, чтобы движущий момент был равен моменту сопротивления качению
 = = 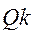 , ,
откуда необходимая движущая сила 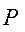 равна равна
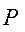 = = 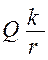 . (6.13) . (6.13)
Величина  называется коэффициентом трения качения. Она измеряется в миллиметрах. На практике считают, что коэффициент трения качения зависит только от материалов касающихся тел. называется коэффициентом трения качения. Она измеряется в миллиметрах. На практике считают, что коэффициент трения качения зависит только от материалов касающихся тел.
Обычно сопротивление качению значительно меньше, чем сопротивление трения скольжения.
№12
12. Механическим коэффициентом полезного действия (КПД) называется отношение работы сил полезного сопротивления к работе движущих сил:
 , (6.15) , (6.15)
где  - коэффициент потерь, который показывает, какая часть работы движущих сил расходуется на преодоление внепроизводственных сопротивлений. - коэффициент потерь, который показывает, какая часть работы движущих сил расходуется на преодоление внепроизводственных сопротивлений.
№13
13 Синтез плоских механизмов с низшими кинематическими парами
Проектирование схемы механизма по заданным его свойствам называется синтезом механизма.
Вначале рассмотрим свойства шарнирного четырехзвенника, являющегося основой многих механизмов.
На рис.5.1,а изображена схема четырехзвенного механизма ABCD, где 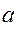 , ,  , , 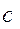 и и  являются длинами соответствующих звеньев. являются длинами соответствующих звеньев.
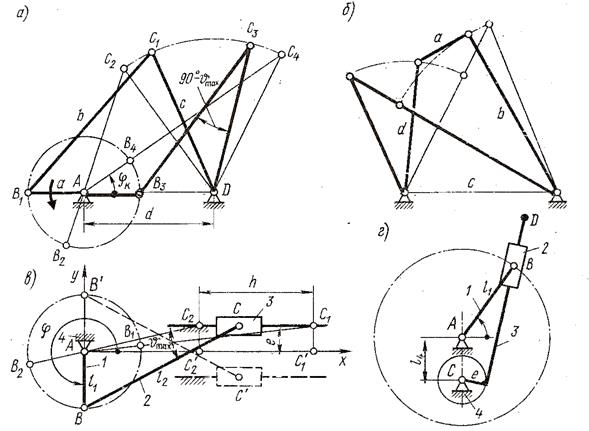
Рис.5.1
Для того, чтобы звено  могло стать кривошипом, оно должно при вращении последовательно пройти через крайние левое ( могло стать кривошипом, оно должно при вращении последовательно пройти через крайние левое (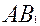 ) и правое ) и правое  положения. положения.
Предполагая, что 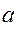 - длина короткого звена, - длина короткого звена,  - самого длинного, и используя соотношение между длинами сторон треугольника (длина стороны треугольника меньше суммы длин двух других его сторон), имеем: - самого длинного, и используя соотношение между длинами сторон треугольника (длина стороны треугольника меньше суммы длин двух других его сторон), имеем:
Из 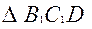
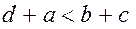 
из 
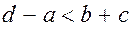 
Независимо от соотношения длин  и и 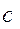 неравенство неравенство  всегда обеспечит выполнение неравенства всегда обеспечит выполнение неравенства  . .
Неравенство  есть условие существования кривошипа. Другими словами, кривошипом может быть наименьшее звено при условии, что сумма длин наименьшего и наибольшего звеньев меньше (или равна) суммы длин двух других звеньев. Это положение носит название правило Грасгофа. есть условие существования кривошипа. Другими словами, кривошипом может быть наименьшее звено при условии, что сумма длин наименьшего и наибольшего звеньев меньше (или равна) суммы длин двух других звеньев. Это положение носит название правило Грасгофа.
Применяя это правило, шарнирные четырехзвенники разбивают на три группы:
а) кривошипно- коромысловый механизм (рис. 5,а);
б) двухкривошипный механизм (стойка звено 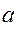 ); );
в) двухкоромысловый механизм (стойка звено 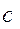 ). ).
Во внеосном кривошипно-ползунном механизме 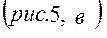 звено звено 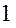 будет кривошипом, если при вращении пройдет положения будет кривошипом, если при вращении пройдет положения 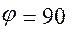 и и  , что возможно при выполнении условия , что возможно при выполнении условия
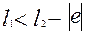 , ,
где  - внеосность (или дезаксиал). Штриховой линией изображена схема, когда - внеосность (или дезаксиал). Штриховой линией изображена схема, когда  . .
В кулисном механизме рис.5.1,г звено 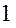 всегда может быть кривошипом: звено всегда может быть кривошипом: звено  (кулиса) будет кривошипом, если при вращении пройдет положение (кулиса) будет кривошипом, если при вращении пройдет положение 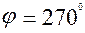 , что возможно при выполнении условия , что возможно при выполнении условия
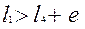 . .
Это будет механизм с вращающейся кулисой. Если   , то кулиса , то кулиса  будет коромыслом (механизм с качающейся кулисой). Обычно в кулисных механизмах будет коромыслом (механизм с качающейся кулисой). Обычно в кулисных механизмах  . .
№14
14 Для того, чтобы звено  могло стать кривошипом, оно должно при вращении последовательно пройти через крайние левое ( могло стать кривошипом, оно должно при вращении последовательно пройти через крайние левое (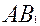 ) и правое ) и правое  положения. положения.
Предполагая, что 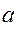 - длина короткого звена, - длина короткого звена,  - самого длинного, и используя соотношение между длинами сторон треугольника (длина стороны треугольника меньше суммы длин двух других его сторон), имеем: - самого длинного, и используя соотношение между длинами сторон треугольника (длина стороны треугольника меньше суммы длин двух других его сторон), имеем:
Из 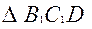
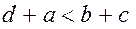 
из 
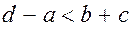 
Независимо от соотношения длин  и и 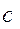 неравенство неравенство  всегда обеспечит выполнение неравенства всегда обеспечит выполнение неравенства  . .
Неравенство  есть условие существования кривошипа. Другими словами, кривошипом может быть наименьшее звено при условии, что сумма длин наименьшего и наибольшего звеньев меньше (или равна) суммы длин двух других звеньев. Это положение носит название правило Грасгофа. есть условие существования кривошипа. Другими словами, кривошипом может быть наименьшее звено при условии, что сумма длин наименьшего и наибольшего звеньев меньше (или равна) суммы длин двух других звеньев. Это положение носит название правило Грасгофа.
№15
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




