|
|
ЛЕКЦИИ 5-6. МОДЕЛИ МОЛЕКУЛЯРНЫХ МАШИНСтр 1 из 6Следующая ⇒ ЛЕКЦИИ 5-6. МОДЕЛИ МОЛЕКУЛЯРНЫХ МАШИН МОЛЕКУЛЯРНЫЕ НОЖНИЦЫ Расщепление пептидной и сложноэфирной связи Без участия фермента в водной среде. Как сказано в эпиграфе любое химическое превращение определяется прежде всего разрывом определенных химических связей. Молекулярные ножницы разрезают химические связи весьма эффективно и при том «в нужном месте и в нужное время». Реакция разрыва химической связи в молекуле А — В (не обязательно двухатомной) на части А и В может происходить в жидкой среде, когда молекула сталкивается с молекулами растворителя. Но этот процесс является маловероятным. Сначала поясним это на примерах разрыва пептидной связи (ПС) в белковой молекуле и сложноэфирной связи в молекуле нейромедиатора ацетилхолина (АХ), находящихся в воде при комнатной температуре. Затем рассмотрим, как эффективно “режут” эти связи молекулы-ножницы (гидролитические ферменты). В процессе пищеварения ПС должны быть разорваны и белковые цепочки расщеплены до аминокислот, которые и попадают в кровь и доставляются с кровотоком ко всем клеткам организма. “Разрезание” сложноэфирной связи в молекуле ацетилхолина с образованием холина и ацетата непрерывно должно происходить в межклеточном пространстве нейронов для поддержания нормального функционирования нервной системы. Мы выбрали эти типичные и вместе с тем замечательные ферменты потому, что их строение (геометрия) в кристаллическом состоянии хорошо известны. Достаточно хорошо изучены также и химические превращения в фермент-субстратном комплексе (ФСК) внутри активного центра (АЦ) этих ферментов. Реакция разрыва пептидной связи может происходить в водном растворе белка. Однако, это очень медленный процесс. Он осуществляется по следующей схеме:

Здесь R1, R2 — остатки двух соседних аминокислот фрагмента пептидной цепи, ПС между которыми (показана волнистой чертой) подлежит разрыву. Более подробно эта реакция записывается следующим образом:
Здесь ПК означает промежуточный комплекс. Такой ПК образуется с участием ионов гидроксила Реакция гидролиза АХ с образованием холина (ХОН) и ацетата
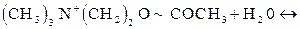
или
Заметим, что АХ и продукты его гидролиза Х Пользуясь выражением для скорости разрыва связи (или образования продукта Р), напишем общую формулу:
Здесь Е — энергия разрываемой связи, [Р] и [OH-] — концентрации продукта и гидроксила. Фактор 1/n, называемый “энтропийным”, является вероятностью того, что атака и сорбция [OH-] произошла “в нужном месте”. Фактор kбT/h определяет среднее число тепловых флуктуаций на разрываемой связи, а m0 зависит от времени сорбции [OH-]. Положим
где DS=-kб ln n. Тогда “абсолютная скорость” запишется в виде:
Здесь F=E-TDS — свободная энергия разрыва связи. Сделаем некоторые оценки. Пусть T=300 K, kT=0,6 ккал = 0,025 эВ = =4 10-13 эрг. Тогда kб T/h=4 1013 Гц. Если положить m0 ~1, то из (1.19) и (1.20) видно, что основной вклад в скорости процессов вносят экспоненциальные множители. Напомним, что для химической связи Е ~100 kб T! Рассмотрим следующую таблицу, показывающую, как зависит Kабс от величины F:
Что бывает, если вместо [OH-] в качестве катализатора выступает фермент? Его роль сводится прежде всего: 1) к изменению энтропийного фактора 1 /n=exp (T D S/kбT); 2) понижению энергетического барьера D Е. При этом для разрыва связи кроме энергии тепловых флуктуаций и энергии сорбции не требуется какого-либо другого источника энергии. Иногда говорят, что большая и сложная молекула фермента представляет собой “структурированный растворитель” для субстрата, который может образовать с молекулой субстрата фермент-субстратный комплекс. Вспоминая слова эпиграфа, можно сказать, что молекула А — В попадает в специально организованное силовое поле и фиксируется в нем. При этом параметры потенциального рельефа все время флуктуируют. Отдельные заряженные колеблющиеся атомы или группы атомов АЦ фермента играют роль гидроксильной группы, которая работает в водном растворе. Потенциальный рельеф в кармане АЦ организован специальным образом: в образовавшемся ФСК величины Е (и D F) снижаются. Атаки разрываемой связи заряженными группами происходят не беспорядочно, как в воде со стороны ОН-, а по фиксированным направлениям. Ниже приводиться разбор физических основ последовательных этапов работы молекулярных ножниц на примере АХТ.
Рис. 1.2. а): «Ленточная» схема молекулы a-химотрипсина (светлые и темные ленты соответствуют b-структурам различных субглобул); АЦ АХТ
Введение
Для иллюстрации возможных приложений рассмотренных выше задач мы выбрали проблему взаимодействия гидролитического фермента ацетилхолинэстеразы (АХЭ) с ее субстратами по ряду причин. Во-первых, АХЭ играет первостепенную роль в процессе синаптической передачи нервных импульсов. Во-вторых, на ее примере видно, какие сложные и разнообразные задачи броуновского движения здесь приходится ставить и решать для понимания ее функционирования как молекулярной машины. Фермент АХЭ, также как a-ХТ, является сериновой гидролазой. Он катализирует быстрый разрыв сложно-эфирной связи в молекуле нейромедиатора ацетилхолина (АХ). Если без a-ХТ невозможны процессы пищеварения, то без АХЭ невозможна синаптическая (химическая) передача электрического возбуждения от одного нейрона к другому или от нервных окончаний к мышечным волокнам. Рассмотрим кратко процесс синаптической передачи. Синапс есть функциональный межмембранный контакт двух возбудимых клеток. В соответствии с механизмом передачи импульса от нейрона к нейрону синапсы делятся на химические, электрические и смешанные. Химические синапсы составляют большую часть синаптического аппарата центральной нервной системы высших животных и человека. Нервно-мышечная передача осуществляется посредством только химических синапсов. Синапсы состоят из трех основных элементов: пресинаптической мембраны, постсинаптической мембраны и синаптической щели (рис. 6.1). Пресинаптической называется мембрана, покрывающая нервное окончание, которое представляет собой своеобразный нейросекреторный аппарат. Здесь содержится и выделяется медиатор, оказывающий возбуждающее или тормозящее воздействие на раздражаемую клетку. В межнейронных синапсах медиатором может служить ацетилхолин (АХ), адреналин, норадреналин, дофамин и некоторые другие вещества. В скелетных мышцах человека, как и всех позвоночных, роль медиатора играет АХ. В пресинаптических окончаниях медиатор АХ содержится в "пузырьках" диаметром около 50 нм. При достижении распространяющегося потенциала действия области пресинаптического окончания АХ освобождается из "пузырьков" и выходит в синаптическую щель. При этом осуществляется принцип: один нервный импульс обеспечивает выход ограниченной порции молекул АХ. Напомним, что импульсы следуют с периодом порядка 1мс. Ширина щели составляет примерно 50 нм. Медиатор быстро диффундирует через щель, воздействуя на мембрану раздражаемой клетки. Та часть мембраны этой клетки, которая непосредственно граничит с нервным окончанием, называется постсинаптической. На постсинаптической мембране расположены ацетилхолиновые рецепторы, отвечающие на действие АХ изменением проницаемости для ионов
Рис. 6.1. Схема передачи нервного импульса в химическом синапсе. 1 - окончание пресинаптического нейрона; 2 - постсинаптический нейрон; 3 - пресинаптическая мембрана; 4 - постсинаптическая мембрана; 5 - синаптическая щель; 6 - пузырьки, содержащие нейромедиатор; 7 - высвобождаемый нейромедиатор; 8 - ацетилхолиновые рецепторы; 9 - фермент ацетилхолинэстераза.
Установлено, что на постсинаптической мембране в больших концентрациях присутствует фермент АХЭ, способный расщеплять АХ на ацетат (А) и холин (Х). Он является одной из разновидностей молекулярных ножниц, о которых мы говорили ранее. Значение этого процесса становится ясным, если учесть, что в естественных условиях к постсинаптической клетке поступают быстро следующие друг за другом нервные импульсы, и постсинаптическая мембрана, деполяризованная предшествующей порцией АХ, становится малочувствительной к действию следующей порции. Чтобы идущие друг за другом нервные импульсы могли осуществлять нормальное возбуждающее действие, необходимо к моменту прихода каждого из них "убрать" предшествующую порцию медиатора. Эту функцию и выполняет АХЭ. Существует ряд фармакологических агентов, обладающих способностью резко угнетать активность АХЭ. Их называют ингибиторами. Они используются для устранения мышечного расслабления при наркозе, а также при заболеваниях типа миастении. С другой стороны, известны отравления людей инсектицидами на основе этих ингибиторов. При этих отравлениях возникают судороги ¾ результат пролонгированной активации ацетилхолинергетических синапсов, особенно в вегетативной нервной системе. Большинство отравляющих веществ направляют свое действие на АХЭ. Таким образом, изучение механизма работы данной молекулярной машины представляет собой важную задачу с точки зрения медицины и полезно для понимания общих принципов ферментативного катализа. На сегодняшний день в Интернете содержится около 20000 статей, посвященных АХЭ.
Математическая модель. Используя результаты рентгеноструктурного анализа, представим фермент набором жестко связанных неподвижных точек, относительное расположение которых соответствует расположению атомов в молекуле AChE. Для сравнения скорости выхода “осколков” из ущелья в случае закрытого и открытого “back door” используем две модели фермента. Первая модель соответствует молекуле AChE с закрытой “back door” и содержит все атомы, определенные рентгеноструктурным анализом. Вторая модель, соответствующая ферменту с открытой “back door”, должна иметь канал, через который продукты реакции могли бы покинуть ущелье активного центра. Поэтому из второй модели необходимо исключить некоторое количество атомов, определенных рентгеноструктурным анализом. Сделаем это следующим образом. Будем считать, что канал имеет цилиндрическую форму, радиус канала примем равным 5 Субстрат и его “осколки” также представим набором жестко связанных точек. Однако, в данном случае для уменьшения времени счета не будем считать подвижные объекты состоящими из большого числа атомов, а отобразим молекулы ацетилхолина и холина в виде гантелей и молекулу ацетата в виде шара. Размеры гантелей и шара определим из результатов рентгеноструктурного анализа для соответствующих молекул. Наделим каждую точку соответствующими массой и зарядом. Ван-дер-ваальсово взаимодействие двух точек, принадлежащих различным объектам (например, ферменту и продукту реакции), представим потенциалом Леннарда-Джонса:
где r - расстояние между точками; константы A и B для различных пар атомов приведены в [1]. Учет ударов молекул растворителя произведем по методу Ланжевена, т. е. введем в уравнения движения случайную силу [17]. Полагая фермент жестко закрепленным, будем описывать трансляционное движение подвижных объектов координатами и скоростями их центров масс. Для описания вращательного движения с центром масс каждого объекта свяжем подвижную систему координат. Ориентируем ее оси таким образом, чтобы тензор инерции принял диагональный вид. Это можно сделать следующим способом. В системе координат, связанной с центром масс, рассчитывается тензор инерции, определяются его собственные вектора и оси новой системы направляются вдоль собственных векторов. Тогда уравнения движения l-го тела запишутся наиболее просто [18]:
Здесь ml - масса тела; xl, yl, zl - координаты центра масс в декартовой системе; Jl1, Jl2, Jl3 - компоненты тензора инерции; Wl1, Wl2, Wl3 - частоты вращений вокруг осей собственной системы координат;
xlx, xly, xlz - проекции случайной силы на оси лабораторной системы координат; zl1, zl2, zl3 - проекции случайного момента сил на оси подвижной системы координат; gl - коэффициент, учитывающий силу вязкого трения; gl1, gl2, gl3 - коэффициенты, учитывающие силу вязкого трения при вращательном движении;
Сила
Здесь В процессе численного счета трансляционное брауново движение моделировалось следующим образом. Через равные интервалы времени Аналогичным образом моделировалось вращательное брауново движение. Через равные интервалы времени В качестве примера рассмотрим определение скорости связывания субстрата с ферментом или константы k1.
§3.4. Определение константы скорости k1.
Константа k1 определяет скорость образования комплекса E^S из независимых молекул фермента и субстрата: w1=k1[E][S]. Воспользуемся следующей схемой определения этой константы. Ограничим область вблизи основного входа в ущелье активного центра непроницаемыми для молекулы субстрата стенками в форме цилиндра (рис. 3.5). Поместим случайным образом в эту область молекулу ACh и промоделируем ее диффузию в поле, порождаемом ферментом. Если z-компонента координат субстрата становится меньше z1, то считаем комплекс E^S образовавшимся. Многократно повторяя данный этап, определим частоту n образования комплекса E^S при условии, что молекула субстрата все время находится в данной области.
Рис. 3.5. Объем, ограничивающий область около входа в активный центр. Субстрат расположен на оси Oz в точке z1.
Пусть средняя по объему концентрация субстрата в выделенной области равняется [S]1. Тогда среднее отношения времени t, когда субстрат находится в выделенной области, ко времени наблюдения T равняется
где V1 - объем выделенной области. Записанное соотношение справедливо при условии [S]1V1<<1; иначе необходимо принимать во внимание те моменты времени, когда в объеме V1 находятся две и более молекул субстрата. Очевидно, при наличии только одной свободной молекулы фермента частота образования комплекса E^S равняется k1[S]; следовательно,
где q - заряд субстрата (+1e). Введем обозначение
тогда
В процессе численного счета объем V1 ограничивался плоскостью z2=35
Рис. 3.6. Зависимость количества образовавшихся E^S-комплексов N от времени моделирования при нулевой ионной силе.
Рис. 3.7. Зависимость константы скорости k1 от ионной силы I. Указанные погрешности соответствуют 66%-му доверительному интервалу.
РЕЗУЛЬТАТ МОДЕЛИРОВАНИЯ С «BACK DOOR»
Рассматривалась возможность объяснения эффекта субстратного торможения увеличением времени выхода продуктов реакции из ущелья. Это рассмотрение могло бы дать ответ на вопрос о том, имеется ли “back door” в молекуле AChE. Действительно, если бы рассчитанное значение [S]опт для молекулы фермента без “back door” оказалось значительно меньше экспериментального, мы имели бы аргумент в пользу наличия дополнительного канала в ущелье активного центра. Однако даже при концентрации субстрата, на порядок превосходящей экспериментальное значение [S]опт, среднее время выхода оставалось на четыре порядка меньше времени, определяющего химические стадии реакции. Таким образом, на основании имеющихся экспериментальных данных мы не можем утверждать, что в молекуле AChE происходит открытие дополнительного канала в ущелье активного центра.
ЗАКЛЮЧЕНИЕ
Таким образом мы рассмотрели математическую модель связывания субстрата. С моделями других этапов работы молекулярных ножниц можно ознакомиться по монографиям [1,2].
ЛЕКЦИИ 5-6. МОДЕЛИ МОЛЕКУЛЯРНЫХ МАШИН МОЛЕКУЛЯРНЫЕ НОЖНИЦЫ   Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам...  Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот...  Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем...  Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|