|
Аналітична геометрія і алгебра
| №
з.п.
| Питання та варіанти відповідей
| Бланк відповідей
| Правильна відповідь
| |
|
|
|
|
|
|
| | 1.
| Знайти суму элементів третього стовпця матриці В.  . .
| a
| b
| с
| d
|
| | a) 34
| b) -18
| с) -26
| d) 28
| | 2.
| Розв’язати систему рівнянь 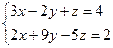 , взявши за базові змінні у і х. , взявши за базові змінні у і х.
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
| | 3.
| Задані вектори 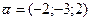 , ,  . Знайти . Знайти  . .
| a
| b
| с
| d
|
| a) 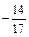
| b) 
| с) 
| d) 0
| | 4.
| Крива другого порядку задана рівнянням  . Визначити тип цієї кривої. . Визначити тип цієї кривої.
| a
| b
| с
| d
|
| | a) еліпс
| b) пара прямих
| с) гіпербола
| d) парабола
| | 5.
| На площині задані дві прямі:  . Встановити їх взаємне розташування. . Встановити їх взаємне розташування.
| a
| b
| с
| d
|
| | a) паралельні
| b) перпендикулярні
| с) утворюють гострий кут
| d) співпадають
| | 6.
|  Яке з наведених значень може бути значенням скалярного добутку векторів Яке з наведених значень може бути значенням скалярного добутку векторів  і і  , зображених на малюнку? , зображених на малюнку?
| a
| b
| с
| d
|
| | a) 0
| b) 3
| с) –2
| d) 
| | 7.
| Векторний добуток  . Що можна сказати про вектори . Що можна сказати про вектори  ? ?
| a
| b
| с
| d
|
| | a) перпендикулярні
| b) паралельні
| с) утворюють гострий кут
| d) компланарні
| | 8.
| Якої розмірності буде матриця, яка є результатом добутку  ? ?
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
| | 9.
| Рівняння прямої, яка проходить через точку  перпендикулярно площині перпендикулярно площині  , має вид: , має вид:
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
| | 10.
| Визначити тип кривої другого порядку  . .
| a
| b
| с
| d
|
| | a) гіпербола
| b) парабола
| с) еліпс
| d) коло
| | 11.
| Що визначає рівняння  у просторі? у просторі?
| a
| b
| с
| d
|
| | a) пряму
| b) точку
| с) площину
| d) дві площини
| | 12.
| Визначити, при яких  і і  прямі прямі  і і  паралельні? паралельні?
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
| | 13.
| Задана пряма у просторі  . Вказати точку, яка належить цій прямій. . Вказати точку, яка належить цій прямій.
| a
| b
| с
| d
|
| | a) (4; 5; 3)
| b) (3; 7; 3)
| с) (3; 5; 6)
| d) (3; 5; 3)
| | 14.
| Знайти рівняння прямої, що проходить через  і і  . .
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
| | 15.
| Відомо, що  , ,  , а кут між , а кут між  і і  дорівнює дорівнює  . Знайти . Знайти  . .
| a
| b
| с
| d
|
| | a) 0
| b) 
| с) 
| d) 0,5
|
Диференціальне числення та диференціальні рівняння
| №
з.п.
| Питання та варіанти відповідей
| Бланк відповідей
| Правильна відповідь
| |
|
|
|
|
|
|
| | 1.
| Сформулюйте геометричний зміст диференціалу функції однієї змінної.
| a
| b
| с
| d
|
| | a) приріст ординати дотичної
| b) тангенс кута нахилу дотичної до осі ОХ
| с) приріст ординати функції
| d) приріст аргументу
| | 2.
| Під яким кутом до осі ОХ направлена дотична до графіка функції  у точці у точці 
| a
| b
| с
| d
|
| a) 
| b) 
| с) 0
| d) 
| | 3.
| Знайти інтервали спадання функції  . .
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
| | 4.
| Матеріальна точка рухається за законом  , де шлях s вимірюється у метрах, а час t – у секундах. Знайдіть швидкість матеріальної точки через 3 секунди після початку руху. , де шлях s вимірюється у метрах, а час t – у секундах. Знайдіть швидкість матеріальної точки через 3 секунди після початку руху.
| a
| b
| с
| d
|
| | a) 11 м/с
| b) 8 м/с
| с) 12 м/с
| d) 6 м/с
| | 5.
| Задане диференціальне рівняння  з початковими умовами з початковими умовами  . Яка з функцій задовольняє цій задачі? . Яка з функцій задовольняє цій задачі?
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
| | 6.
| Встановити тип диференціального рівняння  . .
| a
| b
| с
| d
|
| | a) лінійне;
| b) однорідне
| с) в повних диференціалах
| d) з подільними змінними
| | 7.
| Серед наведених функцій вкажіть неперервну.
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
| | 8.
| Похідна функції має вид  . Яке висловлювання про . Яке висловлювання про  є вірним? є вірним?
| a
| b
| с
| d
|
| | a) функція спадає на всій числовій осі
| b) функція зростає на всій числовій осі
| с) функція має два максимуми
| d) функція має два мінімуми
| | 9.
| Знайти  , якщо , якщо  . .
| a
| b
| с
| d
|
| | a) 4
| b) 1
| с) 0
| d) –1
| | 10.
| Знайти асимптоти кривої  . .
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
| | 11.
| Знайти інтервали опуклості функції  . .
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
| | 12.
| Знайти  , якщо , якщо  , ,  . .
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 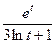
| | 13.
| Функцію  дослідити на екстремум в точках дослідити на екстремум в точках  і і  . .
| a
| b
| с
| d
|
| | a) А – точка максимуму,
В – точка максимуму
| b) А – точка мінімуму,
В не є точкою экстремуму
| с) А – точка мінімуму,
В – точка максимуму
| d) А – точка мінімуму,
В – точка мінімуму
| | 14.
| Задана функція  . Обчислити . Обчислити  . .
| a
| b
| с
| d
|
| a) 
| b) 24
| с) 
| d) 20
| | 15.
| Знайти похідну функції  в точці в точці  в напрямку вектора в напрямку вектора  . .
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
|
Інтегральне числення
| №
з.п.
| Питання та варіанти відповідей
| Бланк відповідей
| Правильна відповідь
| |
|
|
|
|
|
|
| | 1.
| Обчисліть площу поверхні тіла, утвореного обертанням круга навколо осі, що проходить через його центр, якщо діаметр круга дорівнює d.
| a
| b
| с
| d
|
| a) 
| b) 
| с) 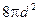
| d) 
| | 2.
| Яким способом можна знайти первісну для функції  ? ?
| a
| b
| с
| d
|
| | a) заміна змінних
| b) частинами
| с) внесення під знак диференціала
| d) за допомогою таблиці
| | 3.
| Відомо, що  . Яка з наведених функцій може бути функцією . Яка з наведених функцій може бути функцією  ? ?
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 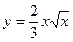
| | 4.
| Знайти  . .
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
| | 5.
| Знайти  . .
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
| | 6.
| Знайти  . .
| a
| b
| с
| d
|
| | a) –2 cos(8x+4)+C
| b) 16 cos(8x+4)+C
| с) sіn(8x+4)+C
| d) cos(8x+4)
| | 7.
| Обчислити площу, обмежену лініями  . .
| a
| b
| с
| d
|
| | a) 8
| b) 8/3
| с) 16/3
| d) 16
| | 8.
|  Знайдіть площу заштрихованої фігури, зображеної на рисунку. Знайдіть площу заштрихованої фігури, зображеної на рисунку.
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
| | 9.
| Знайти об’єм тіла обертання кривої  навколо ОХ. навколо ОХ.
| a
| b
| с
| d
|
| a) 
| b) 4
| с) 
| d) 8
| | 10.
| Знайти  , якщо , якщо  і і  . .
| a
| b
| с
| d
|
| | a) 5
| b) 8
| с) 2
| d) 12
| | 11.
| Функція  , де С– довільна стала, є загальним видом для первісної функції , де С– довільна стала, є загальним видом для первісної функції  При якому значенні С графік первісної проходить через точку При якому значенні С графік первісної проходить через точку  якщо якщо  ? ?
| a
| b
| с
| d
|
| | a) 25
| b) 15
| с) –25
| d) 20
| | 12.
| Відомо, що  При якому найменшому значенні а При якому найменшому значенні а  . .
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
| | 13.
| Упорядкуйте за зростанням величини  . .
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
| | 14.
| Автомобіль рухається прямолінійною ділянкою шосе, причому швидкість його змінюється за законом  де t – час від початку руху в секундах. Яку відстань (у метрах) подолав автомобіль за перші 5 секунд руху? де t – час від початку руху в секундах. Яку відстань (у метрах) подолав автомобіль за перші 5 секунд руху?
| a
| b
| с
| d
|
| | a) 5
| b) 25
| с) 30
| d) 20
| | 15.
| Укажіть формулу для обчислення площі фігури, обмеженої графіком функції  і віссю ОХ. і віссю ОХ.
| a
| b
| с
| d
|
| a) 
| b) 
| с) 
| d) 
|
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




