Площадь криволинейной трапеции

Пусть функция неотрицательна и непрерывна на отрезке . Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью , слева и справа – прямыми и (см. рис. 2) вычисляется по формуле

. (5)

Пример 9. Найти площадь фигуры, ограниченной линией и осью .

Решение. Графиком функции является парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью (прямой ). Для этого решаем систему уравнений

Получаем: , откуда , ; следовательно, , .

Рис. 3

Площадь фигуры находим по формуле (5):

(кв. ед.).

Если функция неположительна и непрерывна на отрезке , то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью , слева и справа – прямыми и , вычисляется по формуле

. (6)

В случае, если функция непрерывна на отрезке и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (рис. 4) равна алгебраической сумме соответствующих определенных интегралов:

. (7)

Рис. 4

Пример 10. Вычислить площадь фигуры, ограниченной осью и графиком функции при .

Рис. 5

Решение. Сделаем чертеж (рис. 5). Искомая площадь представляет собой сумму площадей и . Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему Получим , . Следовательно:

;

.

Таким образом, площадь заштрихованной фигуры равна

(кв. ед.).

Рис. 6

Пусть, наконец, криволинейная трапеция ограничена сверху и снизу графиками непрерывных на отрезке функций и ,
а слева и справа – прямыми и (рис. 6). Тогда ее площадь вычисляется по формуле

. (8)

Пример 11. Найти площадь фигуры, ограниченной линиями и .

Решение. Данная фигура изображена на рис. 7. Площадь ее вычислим по формуле (8). Решая систему уравнений находим , ; следовательно, , . На отрезке имеем: . Значит, в формуле (8) в качестве возьмем x, а в качестве – . Получим:

(кв. ед.).

Более сложные задачи на вычисление площадей решают путем разбиения фигуры на непересекающиеся части и вычисления площади всей фигуры как суммы площадей этих частей.

Рис. 7

Пример 12. Найти площадь фигуры, ограниченной линиями , , .

Решение. Сделаем чертеж (рис. 8). Данную фигуру можно рассматривать как криволинейную трапецию, ограниченную снизу осью , слева и справа – прямыми и , сверху – графиками функций и . Так как фигура ограничена сверху графиками двух функций, то для вычисления ее площади разобьем данную фигуру прямой на две части (1 – это абсцисса точки пересечения линий и ). Площадь каждой из этих частей находим по формуле (4):

(кв. ед.); (кв. ед.). Следовательно:

(кв. ед.).

Рис. 8

Рис. 9

В заключение отметим, что если криволинейная трапеция ограничена прямыми и , осью и непрерывной на кривой (рис. 9), то ее площадь находится по формуле

.

Объем тела вращения

Пусть криволинейная трапеция, ограниченная графиком непрерывной на отрезке функции , осью , прямыми и , вращается вокруг оси (рис. 10). Тогда объем полученного тела вращения вычисляется по формуле

. (9)

Пример 13. Вычислить объем тела, полученного вращением вокруг оси криволинейной трапеции, ограниченной гиперболой , прямыми , и осью .

Решение. Сделаем чертеж (рис. 11).

Из условия задачи следует, что , . По формуле (9) получаем

.

Рис. 10

Рис. 11

Объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной прямыми у = с и у = d, осью Оу и графиком непрерывной на отрезке функции (рис. 12), определяется по формуле

. (10)

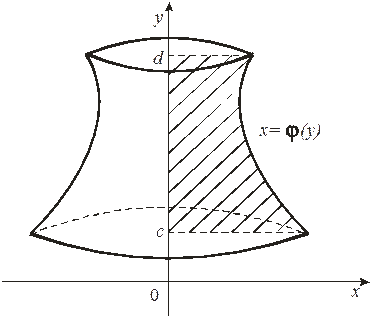
Рис. 12

Пример 14. Вычислить объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной линиями х ² = 4 у, у = 4, х = 0 (рис. 13).

Решение. В соответствии с условием задачи находим пределы интегрирования: , . По формуле (10) получаем:

.

Рис. 13

Длина дуги плоской кривой

Пусть кривая , заданная уравнением , где , лежит в плоскости (рис. 14).

Рис. 14

Определение. Под длиной дуги понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю.

Если функция и ее производная непрерывны на отрезке , то длина дуги кривой вычисляется по формуле

. (11)

Пример 15. Вычислить длину дуги кривой , заключенной между точками, для которых .

Решение. Из условия задачи имеем . По формуле (11) получаем:

.

4. Несобственные интегралы
с бесконечными пределами интегрирования

При введении понятия определённого интеграла предполага-лось, что выполняются следующие два условия:

а) пределы интегрирования а и являются конечными;

б) подынтегральная функция ограничена на отрезке .

Если хотя бы одно из этих условий не выполняется, то интеграл называется несобственным.

Рассмотрим вначале несобственные интегралы с бесконечными пределами интегрирования.

Определение. Пусть функция определена и непрерывна на промежутке , тогда

(12)

называется несобственным интегралом с бесконечным верхним пределом интегрирования (несобственным интегралом I рода).

Если существует и конечен, то несобственный интеграл называется сходящимся; если данный предел не существует или равен , то несобственный интеграл называется расходящимся.

Геометрически несобственный интеграл от неотрицательной функции выражает площадь бесконечной криволинейной трапеции, ограниченной сверху графиком функции , снизу – осью , слева – отрезком прямой и неограниченной справа (рис. 15).

Если несобственный интеграл сходится, то эта площадь является конечной; если несобственный интеграл расходится, то эта площадь бесконечна.

Рис. 15

Аналогично определяется несобственный интеграл с бесконечным нижним пределом интегрирования:

. (13)

Этот интеграл сходится, если предел в правой части равенства (13) существует и конечен; в противном случае интеграл называется расходящимся.

Несобственный интеграл с двумя бесконечными пределами интегрирования определяется следующим образом:

, (14)

где с – любая точка интервала . Интеграл сходится только в том случае, когда сходятся оба интеграла в правой части равенства (14).

Пример 16. Исследовать на сходимость несобственные интегралы:

а) ; б) ; в) ; г) .

Решение. а) , следовательно, данный интеграл расходится;

б)

. Так как при предел не существует, то интеграл расходится;

в)

Значит, несобственный интеграл сходится и его значение равно ;

г) = [выделим в знаменателе полный квадрат: ] = [замена:

] =

Значит, несобственный интеграл сходится и его значение равно .

Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? - задался я вопросом...

ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между...

ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования...

Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем...

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: