Частный институт управления и предпринимательства

Частный институт управления и предпринимательства

В. М. Метельский

ВЫСШАЯ
МАТЕМАТИКА

Определенный интеграл

Минск 2007

Частный институт управления и предпринимательства

В. М. Метельский

ВЫСШАЯ
МАТЕМАТИКА

Определенный интеграл

Учебно-методическое пособие

Минск 2007

УДК 51(075.8):33

ББК 22.1я73

М 54

Рекомендовано к изданию редакционно-издательским советом
Частного института управления и предпринимательства

А в т о р

доцент кафедры высшей математики и статистики

Частного института управления и предпринимательства

кандидат физико-математических наук В. М. Метельский

Метельский, В. М.

М 54 Высшая математика. Определенный интеграл: учеб.-метод. посо-бие / В. М. Метельский. – Минск: Частн. ин-т упр. и предпр., 2007. –
29 с.

Пособие подготовлено в соответствии с учебной программой ЧИУиП по дисциплине «Высшая математика», стандартом и типовой программой Министерства образования Республики Беларусь. Оно включает лекции, задачи, упражнения и индивидуальные задания по теме «Определенный интеграл».

Для студентов дневной и заочной форм обучения Частного института управления и предпринимательства.

УДК 51(075.8):33

ББК 22.1я73

Ó Метельский В. М., 2007

Ó Частный институт управления и предпринимательства, 2007

Лекция 1. оПРЕДЕЛЕННЫЙ иНТЕГРАЛ

План

1. Понятие определенного интеграла.

2. Геометрический смысл определенного интеграла.

3. Основные свойства определенного интеграла.

4. Формула Ньютона–Лейбница.

5. Замена переменной в определенном интеграле.

6. Интегрирование по частям.

Ключевые понятия

Интегральная сумма. Определенный интеграл. Пределы интегрирования. Интегрируемая функция. Криволинейная трапеция. Формула Ньютона–Лейбница. Теорема о среднем.

Понятие определенного интеграла

Пусть функция определена на отрезке , . Выполним следующие операции:

1) разобьем отрезок точками на n частичных отрезков ;

2) в каждом из частичных отрезков , выберем произвольную точку и вычислим значение функции в этой точке: ;

3) найдем произведения , где – длина частичного отрезка , ;

4) составим сумму

, (1)

которая называется интегральной суммой функции y = f(x) на отрезке[а, b]. С геометрической точки зрения интегральная сумма представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки , а высоты равны соответственно (рис. 1). Обозначим через длину наибольшего частичного отрезка ;

5) найдем предел интегральной суммы, когда .

Рис. 1

Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка на частичные отрезки, ни от выбора точек в них, то этот предел называется определенным интегралом от функции на отрезке и обозначается .

Таким образом, .

В этом случае функция называется интегрируемой на . Числа а и b называются соответственно нижним и верхним пределами интегрирования, – подынтегральной функцией, – подынтег-ральным выражением, – переменной интегрирования; отрезок называется промежутком интегрирования.

Теорема 1. Если функция непрерывна на отрезке , то она интегрируема на этом отрезке.

Формула Ньютона–Лейбница

Вычисление определенных интегралов через предел интегральных сумм связано с большими трудностями. Поэтому существует другой метод, основанный на тесной связи, существующей между понятиями определенного и неопределенного интегралов.

Теорема 2. Если функция непрерывна на отрезке и – какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:

, (2)

которая называется формулой Ньютона–Лейбница. Разность принято записывать следующим образом:

,

где символ называется знаком двойной подстановки.

Таким образом, формулу (2) можно записать в виде:

.

Нахождение определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два этапа: на первом этапе находят некоторую первообразную для подынтегральной функции ; на втором –находится разность значений этой первообразной на концах отрезка .

Пример 1. Вычислить интеграл .

Решение. Для подынтегральной функции произвольная первообразная имеет вид . Так как в формуле Ньютона-Лейбни-ца можно использовать любую первообразную, то для вычисления ин-
теграла возьмем первообразную, имеющую наиболее простой вид: . Тогда .

Пример 2. Вычислить интеграл .

Решение. По формуле Ньютона-Лейбница имеем:

.

5. Замена переменной в определенном интеграле

Теорема 3. Пусть функция непрерывна на отрезке . Тогда, если: 1) функция и ее производная непрерывны при ; 2) множеством значений функции при является отрезок ;3) , , то справедлива формула

, (3)

которая называется формулой замены переменной в определенном интеграле.

Пример 3. Вычислить интеграл

Решение. Введем новую переменную по формуле . Определим и . Возведя в квадрат обе части равенства , получим , откуда . Находим новые пределы интегрирования. Для этого в формулу подставим старые пределы и . Получим: , откуда и, следовательно, ; , откуда и, следовательно, . Таким образом:

.

Пример 4. Вычислить интеграл .

Решение. Воспользуемся универсальной тригонометрической подстановкой. Положим , откуда , . Найдем новые пределы интегрирования: если , то ; если , то . Значит, . Следовательно:

.

Пример 5. Вычислить интеграл .

Решение. Положим , тогда , откуда . Находим новые пределы интегрирования: ; . Имеем: . Следовательно:

.

Интегрирование по частям

Теорема 4. Пусть функции и имеют непрерывные производные на отрезке . Тогда имеет место следующая формула интегрирования по частям:

. (4)

Доказательство

Так как , то функция является первообразной для функции . Тогда по формуле Ньютона–Лейбница получаем

,

откуда

.

Пример 6. Вычислить .

Решение. Положим , отсюда . По формуле (4) находим

.

Пример 7. Вычислить .

Решение. Пусть , тогда . Применяя формулу интегрирования по частям, получаем

.

Пример 8. Вычислить .

Решение. Полагая , определяем . Следовательно:

[к полученному интегра-лу снова применяем формулу интегрирования по частям: ; следовательно: ] = =

.

ЗАДАЧИ И УПРАЖНЕНИЯ

Определенный интеграл

1. Вычислить определенные интегралы:

a) ; б) ; в) ; г) ;

д) ; е) ; ж) ; з) ;

и) ; к) ; л) .

2. Применяя метод замены переменной, вычислить следующие интегралы:

а) ; б) ; в) ; г) ;

д) ; е) ; ж) .

3. Применяя метод интегрирования по частям, вычислить следующие интегралы:

а) ; б) ; в) ;

г) ; д) ; е) .

Лекция 2. ПРИМЕНЕНИЕ оПРЕДЕЛЕННЫХ иНТЕГРАЛОВ.

НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

План

1. Площадь криволинейной трапеции.

2. Объем тела вращения.

3. Длина дуги плоской кривой.

4. Несобственные интегралы с бесконечными пределами интегрирования.

5. Несобственные интегралы от неограниченных функций.

Ключевые понятия

Тело вращения. Плоская кривая. Несобственные интегралы. Бесконечные пределы интегрирования. Неограниченная функция. Сходящиеся несобственные интегралы. Расходящиеся несобственные интегралы.

Объем тела вращения

Пусть криволинейная трапеция, ограниченная графиком непрерывной на отрезке функции , осью , прямыми и , вращается вокруг оси (рис. 10). Тогда объем полученного тела вращения вычисляется по формуле

. (9)

Пример 13. Вычислить объем тела, полученного вращением вокруг оси криволинейной трапеции, ограниченной гиперболой , прямыми , и осью .

Решение. Сделаем чертеж (рис. 11).

Из условия задачи следует, что , . По формуле (9) получаем

.

Рис. 10

Рис. 11

Объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной прямыми у = с и у = d, осью Оу и графиком непрерывной на отрезке функции (рис. 12), определяется по формуле

. (10)

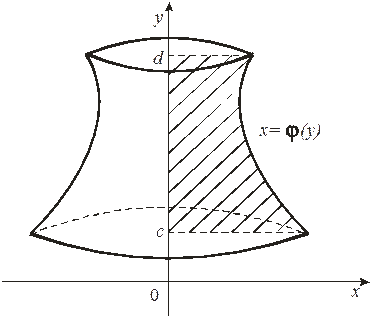
Рис. 12

Пример 14. Вычислить объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной линиями х ² = 4 у, у = 4, х = 0 (рис. 13).

Решение. В соответствии с условием задачи находим пределы интегрирования: , . По формуле (10) получаем:

.

Рис. 13

Длина дуги плоской кривой

Пусть кривая , заданная уравнением , где , лежит в плоскости (рис. 14).

Рис. 14

Определение. Под длиной дуги понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю.

Если функция и ее производная непрерывны на отрезке , то длина дуги кривой вычисляется по формуле

. (11)

Пример 15. Вычислить длину дуги кривой , заключенной между точками, для которых .

Решение. Из условия задачи имеем . По формуле (11) получаем:

.

4. Несобственные интегралы
с бесконечными пределами интегрирования

При введении понятия определённого интеграла предполага-лось, что выполняются следующие два условия:

а) пределы интегрирования а и являются конечными;

б) подынтегральная функция ограничена на отрезке .

Если хотя бы одно из этих условий не выполняется, то интеграл называется несобственным.

Рассмотрим вначале несобственные интегралы с бесконечными пределами интегрирования.

Определение. Пусть функция определена и непрерывна на промежутке , тогда

(12)

называется несобственным интегралом с бесконечным верхним пределом интегрирования (несобственным интегралом I рода).

Если существует и конечен, то несобственный интеграл называется сходящимся; если данный предел не существует или равен , то несобственный интеграл называется расходящимся.

Геометрически несобственный интеграл от неотрицательной функции выражает площадь бесконечной криволинейной трапеции, ограниченной сверху графиком функции , снизу – осью , слева – отрезком прямой и неограниченной справа (рис. 15).

Если несобственный интеграл сходится, то эта площадь является конечной; если несобственный интеграл расходится, то эта площадь бесконечна.

Рис. 15

Аналогично определяется несобственный интеграл с бесконечным нижним пределом интегрирования:

. (13)

Этот интеграл сходится, если предел в правой части равенства (13) существует и конечен; в противном случае интеграл называется расходящимся.

Несобственный интеграл с двумя бесконечными пределами интегрирования определяется следующим образом:

, (14)

где с – любая точка интервала . Интеграл сходится только в том случае, когда сходятся оба интеграла в правой части равенства (14).

Пример 16. Исследовать на сходимость несобственные интегралы:

а) ; б) ; в) ; г) .

Решение. а) , следовательно, данный интеграл расходится;

б)

. Так как при предел не существует, то интеграл расходится;

в)

Значит, несобственный интеграл сходится и его значение равно ;

г) = [выделим в знаменателе полный квадрат: ] = [замена:

] =

Значит, несобственный интеграл сходится и его значение равно .

ЗАДАЧИ И УПРАЖНЕНИЯ

Применение определенных интегралов.
Несобственные интегралы

1. Найти площадь фигуры, ограниченной линиями:

a) и осью Ox; б) ;

в) и ; г) и ;

д) и ; е) и ;

ж) и ; з) и ;

и) ; к) и ;

л) и ; м) .

2. Вычислить объем тела, полученного вращением вокруг оси Ох криволинейной трапеции, ограниченной линиями:

а) где ; б) ;

в) ; г) ;

д) ; е) .

3. Вычислить объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной линиями:

а) ; б) ;

в) ; г) ;

д) ; е) .

4. а) вычислить длину дуги кривой , заключенной между точками, для которых .

б) вычислить длину дуги кривой , заключенной между точками, для которых .

5. Исследовать на сходимость несобственные интегралы:

а) ; б) ; в) ; г) ;

д) ; е) ; ж) ; з) ;

и) ; к) ; л) ; м) .

Литература

1. Ильин В. А., Позняк Э. Г. Основы математического анализа. Ч. I. – М.: Наука, 1982. – 616 с.

2. Гусак А. А. Математический анализ и дифференциальные уравне-ния.– Мн.: ТетраСистемс, 1998. – 416 с.

3. Гусак А. А. Высшая математика: Учеб. пособие для студентов вузов: В 2 т. – Мн., 1998. – 544 с. (1 т.), 448 с. (2 т.).

4. Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Высшая математика для экономистов: Учебник для вузов / Под ред. проф. Н. Ш. Кремера.– М.: ЮНИТИ, 2002. – 471 с.

5. Яблонский А. И., Кузнецов А. В., Шилкина Е. И. и др. Высшая математика. Общий курс: Учебник / Под общ. ред. С. А. Самаля.– Мн.: Выш. шк., 2000. – 351 с.

ОТВЕТЫ К ЗАДАЧАМ И УПРАЖНЕНИЯМ

Определенный интеграл

1. а) ; б) 1; в) 6; г) 1; д) ; е) ; ж) ; з) 40; и) ; к) ; л) .

2. а) ; б) ; в) ; г) ; д) ; е) ; ж) 2.

3. a) ; б) ; в) ; г) ; д) ; е) .

Применение определенных интегралов.
Несобственные интегралы

1. а) ; б) ; в) ; г) ; д) ; е) ; ж) 27; з) ; и) ; к) 36; л) 4,5; м) .

2. а) ; б) ; в) ; г) ; д) ; е) .

3. а) ; б) ; в) ; г) ; д) ; е) .

4. а) ; б) .

5. а) 1; б) расходится; в) ; г) расходится; д) ; е) 0,5; ж) 2; з) ; и) расходится; к) расходится; л) -1; м) расходится.

СОДЕРЖАНИЕ

Лекция 1. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ................................................................. 3

1. Понятие определенного интеграла............................................... 3

2. Геометрический смысл определенного интеграла....................... 4

3. Основные свойства определенного интеграла............................ 5

4. Формула Ньютона–Лейбница...................................................... 6

5. Замена переменной в определенном интеграле.......................... 7

6. Интегрирование по частям........................................................... 9

Задачи и упражнения. Определенный интеграл.............................. 10

Лекция 2. ПРИМЕНЕНИЕ оПРЕДЕЛЕННЫХ иНТЕГРАЛОВ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ ................................................................................................ 11

1. Площадь криволинейной трапеции.............................................. 11

2. Объем тела вращения.................................................................... 17

3. Длина дуги плоской кривой......................................................... 20

4. Несобственные интегралы с бесконечными пределами интегрирования 21

5. Несобственные интегралы от неограниченных функций............ 23

Задачи и упражнения. Применение определенных интегралов. Несобственные интегралы.................................................................................................. 25

Литература...................................................................................... 26

Ответы к задачам и упражнениям................................................. 27

Учебное издание

ВЫСШАЯ МАТЕМАТИКА

Определенный интеграл

Учебно-методическое пособие

Ответственный за выпуск И. В. Лаврик

Компьютерный набор В. М. Метельский

Компьютерная верстка С. Л. Дудко

Корректор Н. А. Бебель

Подписано в печать 17.08.2007 г. Формат 60х84¹/₁₆.

Бумага газетная. Гарнитура «Times New Roman».

Отпечатано способом ризографии в авторской редакции.

Усл. печ. л. 1,68. Уч.-изд. л. 1,45. Тираж 250 экз. Заказ 91.

Издатель и полиграфическое исполнение:

Учреждение образования

«Частный институт управления и предпринимательства».

220086, г. Минск, ул. Славинского 1, корп. 3.

Лицензия ЛИ № 02330/0133342 от 29.06.2004 г.

Частный институт управления и предпринимательства

В. М. Метельский

ВЫСШАЯ
МАТЕМАТИКА

Определенный интеграл

Минск 2007

Частный институт управления и предпринимательства

В. М. Метельский

ВЫСШАЯ
МАТЕМАТИКА

Определенный интеграл

Учебно-методическое пособие

Минск 2007

УДК 51(075.8):33

ББК 22.1я73

М 54

Рекомендовано к изданию редакционно-издательским советом
Частного института управления и предпринимательства

А в т о р

доцент кафедры высшей математики и статистики

Частного института управления и предпринимательства

кандидат физико-математических наук В. М. Метельский

 

 

Р е ц е н з е н т ы:

 

профессор кафедры высшей математики
Белорусского государственного экономического университета
доктор физико-математических наук, профессор Н. С. Коваленко;

 

доцент кафедры высшей математики
Белорусского национального технического университета
кандидат физико-математических наук, доцент Т. И. Чепелева

 

 

Р

1234Следующая ⇒

Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...

ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования...

Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычис­лить, когда этот...

ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между...

---

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: