|
|
ВВЕДЕНИЕ В ИНФОРМАТИКУ И ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИСтр 1 из 6Следующая ⇒ ВВЕДЕНИЕ В ИНФОРМАТИКУ И ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
Часть 1
Методические указания к выполнению лабораторных работ по дисциплинам «Информатика», «Информационные технологии» для студентов очной и заочной формы обучения направлений 040400.62, 030900.62, 040100.62, 190700.62, 140400.62, 190600.62, 190109.65, 190110.65, 151900.62, 150700.62, 220700.62, 220400.62, 280700.62, 221700.62
Курган 2014
Кафедра: «Информатика» Дисциплина: «Информатика», «Информационные технологии» (направления 040400.62, 030900.62, 040100.62, 190700.62, 140400.62, 190600.62, 190109.65, 190110.65, 151900.62, 150700.62, 220700.62, 220400.62, 280700.62, 221700.62)
Составили: ст. преподаватель Л.Г. Сысолятина, ст. преподаватель В.Я. Котликова, ст. преподаватель М.Б. Бекишева Утверждены на заседании кафедры «19» ноября 2013 г. Рекомендованы методическим советом университета «__» марта 2014 г.
Содержание
1 Методы и модели оценки количества информации. 4 1.1 Объемный способ измерения информации. 4 1.2 Энтропийный способ измерения информации. 4 1.3 Энтропия и информация. 6 1.4 Информация и алфавит. 8 2 Системы счисления. 10 2.1 Понятие о системах счисления. 10 2.2 Представление чисел в позиционных системах счисления. 11 2.3 Перевод целых чисел из одной системы счисления в другую.. 13 2.4 Перевод дробных чисел из одной системы счисления в другую.. 14 2.5 Перевод смешанных чисел. 16 2.6 Перевод чисел между системами счисления 2«8«16. 17 2.7 Арифметические операции. 18 3 Основы алгоритмизации. 23 3.1 Алгоритм и его свойства. 23 3.2 Правила выполнения схем. 24 3.3 Фрагменты ГОСТ 19.003-80 Перечень, наименование, обозначение символов и отображаемые ими функции. 25 3.4 Основные типы алгоритмических структур. 27 3.4.1 Линейный алгоритм. 27 3.4.2 Алгоритмическая структура «Ветвление». 28 3.4.3 Алгоритмическая структура «Выбор». 29 3.4.4 Алгоритмическая структура «Цикл». 29 3.5 Примеры.. 31
Методы и модели оценки количества информации Информация является одной из исходных категорий мироздания. Информацию наряду с веществом и энергией рассматривают в качестве важнейшей сущности мира, в котором мы живем. Определение информации невозможно свести к каким-то более простым, более исходным терминам. Аналогичными неопределяемыми понятиями, например, в математике являются точка или прямая. Можно сделать некоторые утверждения, связанные с этими математическими понятиями, но определить их с помощью более элементарных понятий нельзя. На бытовом уровне и во многих научных дисциплинах термин «информация» ассоциируется с понятиями сведения, данные, знание, сообщения и др. Объемный способ измерения информации Объем информации в сообщении – это количество символов в сообщении. Поскольку одно и то же число может быть записано разными способами (с использованием различных алфавитов): тридцать два, 32, XXXII, 1000002, то этот способ чувствителен к форме представления сообщения. В вычислительной технике вся обрабатываемая и хранимая информация вне зависимости от ее природы (число, текст, звук и т.д.) представлена в двоичной форме. Такая стандартизация позволила ввести две стандартные единицы измерения: бит и байт. Энтропия и информация Итак, мы определили энтропию как меру неопределенности состояния некоторой физической системы. Очевидно, что в результате получения сведений неопределенность системы может быть уменьшена. Чем больше объем полученных сведений, чем более содержательны сведения, тем больше информации о системе, тем менее неопределенным будет состояние системы. Естественно поэтому количество информации измерять уменьшением энтропии той системы, для уточнения состояния которой предназначены сведения. Рассмотрим некоторую системы Х, над которой производится наблюдение, и оценим информацию, получаемую в результате того, что состояние системы Х становится полностью известным. До получения информации энтропия системы была H(X). После получения сведений состояние системы полностью определилось, т.е. энтропия стала равной нулю. Обозначим Ix информацию, получаемую в результате выяснения состояния системы Х. Она равна уменьшению энтропии: Ix=H(x) – 0 или Ix = H(X), (1.4) Информация и алфавит Алфавитный подход к измерению информации позволяет определить количество информации, заключенной в тексте. Алфавитный подход является объективным, т. е. он не зависит от субъекта (человека), воспринимающего текст. Множество символов, используемых при записи текста, называется алфавитом. Полное количество символов в алфавите называется мощностью (размером) алфавита. Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ, вычисляется по формуле: x = log2N, (т. к. N = 2х), где N – мощность алфавита. Следовательно, в 2-символьном алфавите каждый символ «весит» 1 бит (log22 = 1); в 4-символьном алфавите каждый символ несет 2 бита информации (log24 = 2); в 8-символьном – 3 бита (log28 = 3) и т. д. один символ из алфавита мощностью 256 (28) несет в тексте 8 бит информации. Такое количество информации называется байт. Алфавит из 256 символов используется для представления текстов в компьютере. 1 байт = 8 бит. Если весь текст состоит из К символов, то при алфавитном подходе размер содержащейся в нем информации равен: V = K x, где x – информационный вес одного символа в используемом алфавите. Для измерения информации используются и более крупные единицы: 1 Кбайт (килобайт) = 210 байт = 1024 байта 1 Мбайт (мегабайт) = 220 байт = 1024 Кбайта 1 Гбайт (гигабайт) = 230 байт = 1024 Мбайта 1 Тбайт (терабайт) = 240 байт = 1024 Гбайта
пример 4 книга, набранная с помощью компьютера, содержит 150 страниц; на каждой странице – 40 строк, в каждой строке – 60 символов. Каков объем информации в книге? Решение. Мощность компьютерного алфавита равна 256. один символ несет 1 байт информации. Значит, страница содержит 40 х 60 = 2400 байт информации. Объем информации в книге (в разных единицах): 2400 х 150 = 3600 байт. 360000/1024 = 351,5625 Кбайт. 351,5625/1024 = 0,34332275 Мбайт. Системы счисления Понятие о системах счисления Любое число имеет значение (содержание) и форму представления. Значение числа задает его отношение к значениям других чисел («больше», «меньше», «равно») и, следовательно, порядок расположения чисел на числовой оси. Форма представления определяет порядок записи числа с помощью предназначенных для этого знаков. При этом значение числа не зависит от способа его представления. Число с одним и тем же значением может быть записано по-разному, т.е. отсутствует взаимно однозначное соответствие между представлением числа и его значением. В связи с этим возникают вопросы о формах представления чисел и о способах перехода от одной формы к другой. Способ представления числа определяется системой счисления. Система счисления — это совокупность приемов и правил для обозначения и наименования чисел. • Алфавит системы счисления — это множество всех символов (знаков), используемых для записи чисел в данной системе счисления. • Цифра — это любой символ (знак), входящий в алфавит данной системы счисления. Системы счисления делятся на следующие виды: 1) унарные системы; 2) кодовые (непозиционные) системы; 3) позиционные системы. Простейшая и самая древняя — так называемая унарная система счисления. В ней для записи любых чисел используется всего один символ. Длина записи числа при таком кодировании прямо связана с его величиной. Представление чисел в позиционных системах счисления Перевод смешанных чисел Перевод смешанных чисел, содержащих целую и дробную части, осуществляется в два этапа. Отдельно переводится целая часть, отдельно – дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой (точкой). Пример 8. Перевести число 17,2510 в двоичную систему счисления. Решение. Переводим целую часть: Переводим дробную часть:
 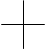 17 2 17 2
0 4 2
0 1
Ответ: 17,2510=10001,012. Общее правило перевода целых чисел из системы счисления с основанием 10 в систему счисления с основанием q: 1) основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления; 2) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, меньшее делителя; 3) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствии с алфавитом новой системы счисления; 4) составить число в новой системе счисления, записывая его начиная с последнего остатка. Здесь и далее под исходной подразумевается система счисления с основанием 10, под новой – с основанием q. Общее правило перевода правильной дроби: из системы счисления с основанием 10 в систему счисления с основанием q: 1) основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления; 2) последовательно умножать данное число и получаемые дробные части произведений на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равной нулю или пока не будет достигнута требуемая точность представления числа; 3) полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствии с алфавитом новой системы счисления; 4) составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения. Арифметические операции Сложение Таблицы сложения для двоичной, восьмеричной и шестнадцатеричной систем счисления представлены на рисунке 2.1. При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево. Сложение Сложение Вычитание Пример 13. Вычесть единицу из чисел 102, 108 и 1016. Решение. Двоичная: 102 – 12 Восьмеричная: 108 – 18 Шестнадцатеричная 1016–116 102 108 1016
Пример 14. Вычесть число 59,75 из числа 201,25 в двоичной, восьмеричной и шестнадцатеричной системах счисления. Решение. Двоичная: 11001001,012–111011,112 Восьмеричная: 311,28–73,68 11001001,01 311,2 – 00111011,11 – 73,6
Шестнадцатеричная C9,416+3B,C16 C9,4 – 3B,C 8D,8 Ответ: 201,2510–59,7510=141,510=10001101,12=215,48=8D,816. Проверка. Преобразуем полученные суммы к десятичному виду: 10001101,12=27+23+22+20+2-1=141,510; 215,48=2*82+1*81+5*80+4*8-1=141,510; 8D,816=8*161+D*160+8*16-1=141,510. умножение Выполняется умножение многозначных чисел в различных позиционных систем счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо брать из соответствующих рассматриваемой системе таблиц умножения и сложения. Таблицы умножения для двоичной, восьмеричной и шестнадцатеричной систем счисления представлены на рисунке 2. Умножение умножение Деление Деление в любой позиционной системе счисления производится по тем же правилам, как и деление в десятичной позиционной системе. В двоичной системе деление выполняется особенно просто, так как очередная цифра частного может быть только нолем или единицей. Пример 16.Разделим число 586510 на число 11510, представив исходные данные в двоичной, восьмеричной и шестнадцатеричной системах счисления. Решение. Двоичная: 10110111010012:11100112 Восьмеричная: 133518:1638
_ 1011011101001 |1110011 _ 13351 | 163 1110011 110011 1262 63 _ 10001000 _ 531 1110011531 _ 10101100 0 1110011 _ 1110011 1111011 Шестнадцатеричная 16Е916: 7316 _ 16Е9 | 73 159 33 _ 159 159 Ответ: 586510:11510=5110=1100112=638=3316. Проверка. Преобразуем полученные суммы к десятичному виду: 1100112=25+24+21+21=5110; 638=6*81+3*80=5110; 3316=3*161+3*160=5110. Основы алгоритмизации Алгоритм и его свойства Прежде чем обратиться к рассмотрению конкретных алгоритмов, необходимо определиться с тем, что же такое алгоритм. Традиционно считается, что самый первый алгоритм был придуман древнегреческим математиком Евклидом. В современной математике понятие алгоритма является ключевым понятием, которое восходит к работам выдающегося узбекского математика IX века Аль-Хорезми. Примеры алгоритмов в широком смысле этого слова можно встретить и в повседневной жизни. Так, поваренная книга является сборником алгоритмов, описывающих процессы приготовления пищи. Компьютерные программы представляют собой алгоритмы, записанные средствами языков программирования. Исчерпывающее определение алгоритма дано выдающимся соотечественником А. А Марковым. алгоритм – это точное общепринятое предписание, определяющее процесс преобразования исходных данных в искомый результат. Исполнитель алгоритма –это тот объект или субъект, для управления которым составлен алгоритм. Система команд исполнителя (СКИ) – это вся совокупность команд, которые исполнитель умеет выполнять. Алгоритм должен обладать следующими свойствами: понятностью, точностью, конечностью. Понятность: алгоритм составляется только из команд, входящих в СКИ исполнителя. Точность: каждая команда алгоритма управления определяет однозначное действие исполнителя. Конечность (или результативность): выполнениеалгоритма должно приводить к результату за конечное число шагов. Среда исполнителя: обстановка, в которой функционирует исполнитель. Определенная последовательность действий исполнителя всегда применяется к некоторым исходным данным. Например: для приготовления блюда по кулинарному рецепту нужны соответствующие продукты (данные). Полный набор данных: необходимый и достаточный набор данных для решения поставленной задачи (получения искомого результата). для того чтобы сделать алгоритм более наглядным, часто используют блок-схемы. Блок-схема алгоритма представляет собой систему блоков, соединенных между собой линиями, которые указывают последовательность выполнения блоков. Направление на линии связи между блоками указывается стрелкой в конце линии. Если линия связи направлена сверху вниз и слева направо, то стрелка на этой линии не ставится. Блоки изображаются геометрическими фигурами, внутри которых дается текстоформульная информация. Блок, организующий ввод или вывод данных, изображается параллелограммом. Для изображения разветвления используется ромб, внутри которого условие разветвления. для обозначения начала и конца алгоритма используются прямоугольники с закругленными углами. Допускается нумерация блоков путем разрыва верхней стороны их контура и записи на месте разрыва номера блока. При составлении блок-схемы алгоритма рекомендуется располагать ее на одной странице и придерживаться правил, установленных ГОСТ 19.002-80 «Схемы алгоритмов и программ. Правила выполнения», ГОСТ 19.003-80 «Схемы алгоритмов и программ. Обозначения условные графические» и ГОСТ 19.701-90 «Единая система программной документации. СХЕМЫ АЛГОРИТМОВ, ПРОГРАММ, ДАННЫХ И СИСТЕМ. Обозначения условные и правила выполнения», дата введения которого 01.01.92. ГОСТ 19.701-90 имеет статус действующего в настоящее время, разработан на основе ГОСТ 19.002-80 и ГОСТ 19.003-80. ОБЩИЕ ТРЕБОВАНИЯ: – Схемы алгоритмов, программ данных и систем состоят из имеющих заданное значение символов, краткого пояснительного текста и соединяющих линий. – Схемы могут использоваться на различных уровнях детализации, причем число уровней зависит от размеров и сложности задачи обработки данных. Уровень детализации должен быть таким, чтобы различные части и взаимосвязь между ними были понятны в целом. – Схема – графическое представление определения, анализа или метода решения задачи, в котором используются символы для отображения операций, данных, потока, оборудования т.д. Правила выполнения схем 1.1 Для облегчения вычерчивания и нахождения на схеме зон устанавливают с учетом минимальных размеров символов, изображенных на данном листе. Допускается один символ размещать в двух и более зонах, если размер символа превышает размер зоны. 1.2 Координаты зоны представляют: по горизонтали – арабскими цифрами слева направо в верхней части листа; по вертикали – прописными буквами латинского алфавита сверху вниз в левой части листа. 1.3 Координаты зон в виде сочетания букв и цифр присваиванию символам, вписанным в поля этих зон, например, А1, А2, А3, В1, В2, В3 и т.д. При выполнении схем от руки, если поле листа не разбито на зоны, символам присваивают порядковые номера. 1.4 В пределах одной схемы, при выполнении ее от руки, допускается применять не более двух смежных размеров ряда чисел, кратных 5. 1.5 Линии потока должны быть параллельны линиям внешней рамки схемы. 1.6 Расстояние между параллельными линиями потока должны быть не менее 3 мм, между остальными символами схемы – не менее 5 мм. 1.7 Записи внутри символа или рядом с ним должны быть краткими. Сокращения слов и аббревиатуры, за исключением установленных государственными стандартами, должны быть расшифрованы в нижней части поля схемы или в документе, к которому эта схема относится. 1.8 Для удобства детализации программы должны быть использованы символы «Процесс», «Решение», «Модификация», «Ввод-вывод» и «Пуск-останов», при этом внутри символов на расстоянии не менее 0,25 а проводят тонкую линию (размер а по ГОСТ 19.003-80) 1.9 Записи внутри символов должны быть представлены так, чтобы их можно было читать слева направо и сверху вниз, независимо от направления потока. Вид а должен быть прочитан как вид б.
а б 3.3 Фрагменты ГОСТ 19.003-80 1 Перечень, наименование, обозначение и размеры обязательных символов и отображаемые ими функции в алгоритме и программе обработки данных должны соответствовать параметрам, указанным в таблице 3.1. Таблица 3.1 – Фрагменты ГОСТ 19.003-80
Размер а должен выбираться из ряда 10, 15, 20 мм. Допускается увеличивать размер а на число, кратное 5. Размер b равен 1,5 а. Линейный алгоритм Алгоритм, в котором команды выполняются последовательно одна за другой, называется линейным алгоритмом. Линейный алгоритм может быть построен из команд присваивания, ввода и вывода.
Пример: x:=5 Переменной X присваивается значение, равное 5.
Пример: ввод А–ввод значения переменной А с клавиатуры компьютера.
Пример: вывод Х–значение переменной Х выводится на экран. На блок-схеме изображена структура линейного алгоритма.
Примеры Пример 1. Даны две простые дроби. Составить алгоритм получения дроби, являющейся результатом их деления. Решение В алгебраической форме решение задачи выглядит следующим образом:
Исходными данными являются четыре целые величины: а, b, с, d. Результат – два целых числа m и n.
Тест: a = 3, b=4, c=5, d=6. Результат: m = 18, n = 20. Пример 2 Даны три вещественных числа А, В, С. Найти наибольшее среди них. Сначала определяется большее среди двух значений А и В, затем большее между найденным значением и величиной С. Алгоритм имеет структуру двух последовательных ветвлений.
Тест: a = 3, b = 6, c = 2. Результат: D = 6. Пример 3 Дано целое положительное число N. Вычислить факториал этого числа: N! = 1 * 2 * 3 *... * N Решение Задача решается c помощью циклического алгоритма: цикла с параметром.
Тест: N = 5. Результат: факториал F = 120. Пример 4 вычислить значение функции Y = A = BX + CX2 для
Пример 5 Использование вложенных циклов на примере вычисления двойной суммы
А= В = (b1, b2, b3, …, bk) – одномерный массив (вектор) данных одного и того же типа.
Замечание. В соответствии с ГОСТ 19.701-90 границы цикла можно изображать следующим образом:
Начало цикла и конец цикла – оба символа имеют один и тот же идентификатор. Условия инициализации, приращения, завершения и т.д. помещаются внутри графического символа в начале или в конце в зависимости от расположения операции, проверяющей условие.
Котликова Вера Яковлевна Сысолятина Лидия Геннадьевна Бекишева Марина Борисовна
ВВЕДЕНИЕ В ИНФОРМАТИКУ И ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
Часть 1
Методические указания к выполнению лабораторных работ по дисциплинам «Информатика», «Информационные технологии» для студентов очной и заочной формы обучения направлений 040400.62, 030900.62, 040100.62, 190700.62, 140400.62, 190600.62, 190109.65, 190110.65, 151900.62, 150700.62, 220700.62, 220400.62, 280700.62, 221700.62
Курган 2014
Кафедра: «Информатика» Дисциплина: «Информатика», «Информационные технологии» (направления 040400.62, 030900.62, 040100.62, 190700.62, 140400.62, 190600.62, 190109.65, 190110.65, 151900.62, 150700.62, 220700.62, 220400.62, 280700.62, 221700.62)
Составили: ст. преподаватель Л.Г. Сысолятина, ст. преподаватель В.Я. Котликова, ст. преподаватель М.Б. Бекишева Утверждены на заседании кафедры «19» ноября 2013 г. Рекомендованы методическим советом университета «__» марта 2014 г.
Содержание
1 Методы и модели оценки количества информации. 4 1.1 Объемный способ измерения информации. 4 1.2 Энтропийный способ измерения информации. 4 1.3 Энтропия и информация. 6 1.4 Информация и алфавит. 8 2 Системы счисления. 10 2.1 Понятие о системах счисления. 10 2.2 Представление чисел в позиционных системах счисления. 11 2.3 Перевод целых чисел из одной системы счисления в другую.. 13 2.4 Перевод дробных чисел из одной системы счисления в другую.. 14 2.5 Перевод смешанных чисел. 16 2.6 Перевод чисел между системами счисления 2«8«16. 17 2.7 Арифметические операции. 18 3 Основы алгоритмизации. 23 3.1 Алгоритм и его свойства. 23 3.2 Правила выполнения схем. 24 3.3 Фрагменты ГОСТ 19.003-80 Перечень, наименование, обозначение символов и отображаемые ими функции. 25 3.4 Основные типы алгоритмических структур. 27 3.4.1 Линейный алгоритм. 27 3.4.2 Алгоритмическая структура «Ветвление». 28 3.4.3 Алгоритмическая структура «Выбор». 29 3.4.4 Алгоритмическая структура «Цикл». 29 3.5 Примеры.. 31
  Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...  Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот...  ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры...  Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|