|
Смешанного умножения векторов
Г10.    , , 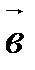 , , 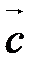 компланарны. компланарны.
Пусть  . Тогда . Тогда    . .
По определению векторного произведения  и и  . .
Следовательно, векторы  , , 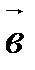 , , 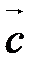 параллельны плоскости, перпендикулярной вектору параллельны плоскости, перпендикулярной вектору  (рис. 24),т.е. векторы (рис. 24),т.е. векторы  , , 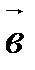 , , 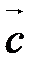 компланарны. компланарны.
Обратно, пусть векторы  , , 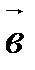 и и 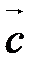 компланарны. Тогда существует плоскость компланарны. Тогда существует плоскость  , которой они параллельны. , которой они параллельны.
 , ,  Þ Þ 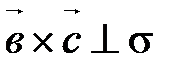 , а так как , а так как  || ||  , то , то  Þ Þ  , ,
т.е.  . .
Г20 (геометрический смысл модуля смешанного произведения). Если векторы  , , 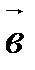 , , 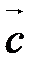 некомпланарны, то абсолютная величина их смешанного произведения равна объему V параллелепипеда с ребрами некомпланарны, то абсолютная величина их смешанного произведения равна объему V параллелепипеда с ребрами  , , 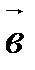 , , 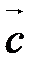 , отложенными от одной точки; , отложенными от одной точки;  , если тройка , если тройка  , , 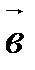 , , 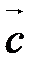 - правая, - правая,  , если тройка , если тройка  , , 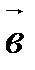 , , 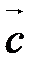 - левая. - левая.
Пусть векторы  , , 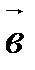 , , 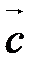 отложены от точки О (рис. 25). отложены от точки О (рис. 25).
 . Пусть . Пусть 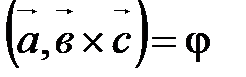 . .
Построим на векторах  , , 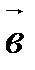 , , 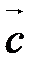 параллелепипед. За основание этого параллелепипеда примем параллелограмм со сторонами параллелепипед. За основание этого параллелепипеда примем параллелограмм со сторонами 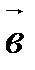 и и 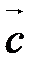 (рис. 26). (рис. 26).
Пусть n – луч, перпендикулярный основанию параллелепипеда и лежащий в том же полупространстве, что и вектор  . Пусть h – высота параллелепипеда. . Пусть h – высота параллелепипеда.
а) Если тройка  , , 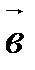 , , 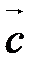 ориентирована так же, как базис ориентирована так же, как базис  , ,  , ,  , то , то 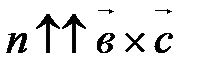 (рис. 26, а) Þ (рис. 26, а) Þ  < 900 Þ cos < 900 Þ cos  >0 Þ >0 Þ 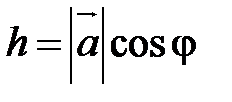 Þ Þ Þ Þ  . .
Итак,  . .
б) Если тройка  , , 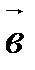 , , 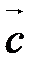 ориентирована противоположно базису ориентирована противоположно базису  , ,  , ,  , то , то  (рис. 26, б) Þ (рис. 26, б) Þ  > 900 Þ > 900 Þ  Þ Þ Þ Þ  . .
Итак,  . .
Из пунктов а) и б) следует, что 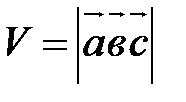 . .
Алгебраические свойства
Смешанного умножения векторов
А10. Циклическая перестановка сомножителей не меняет смешанного произведения, т.е.   V. V.
Перестановка двух соседних сомножителей меняет знак смешанного произведения на противоположный, т.е.
 , ,  V. V.
Для доказательства достаточно применить доказательство свойства Г20 к  и к и к 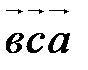 . Параллелепипед будет тот же, только за основание будет принята другая грань (в первом случае – построенная на векторах . Параллелепипед будет тот же, только за основание будет принята другая грань (в первом случае – построенная на векторах 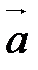 и и 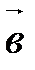 , во втором – на векторах , во втором – на векторах  и и 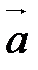 ). ).
Чтобы доказать вторую часть свойства, надо воспользоваться определением смешанного произведения и свойством А10 векторного умножения, а затем совершить циклическую перестановку:
 . .
А20.   V V  . .
Для доказательства этого свойства нужно доказать три равенства:
 ; ; 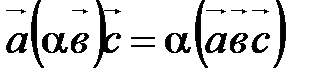 ; ;  . .
Докажите их самостоятельно, пользуясь определением смешанного произведения и алгебраическими свойствами скалярного и векторного умножения векторов.
А30.  ; ;
 ; ;
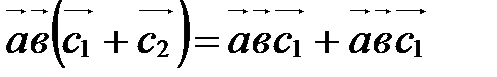 . .
Докажите эти равенства самостоятельно, пользуясь определением смешанного произведения и алгебраическими свойствами скалярного и векторного умножения векторов.
Замечание. Смешанное произведение 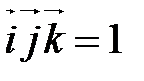 . .
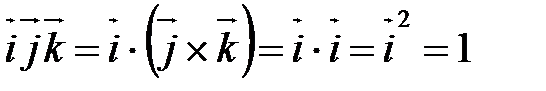 , т.к. , т.к. 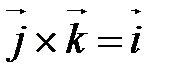 . .
Теорема 1(смешанное произведение в координатах). Если 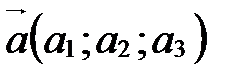 , ,  , , 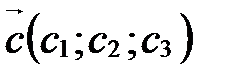 в базисе в базисе  , ,  , ,  , то , то  . .
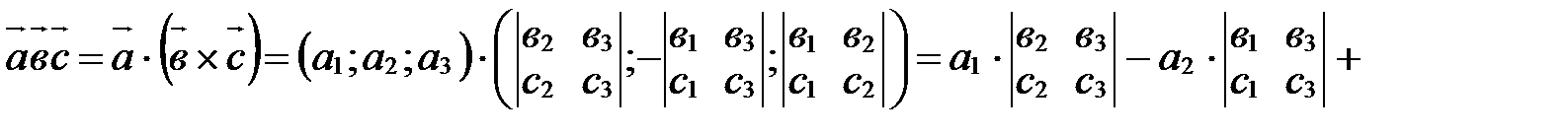 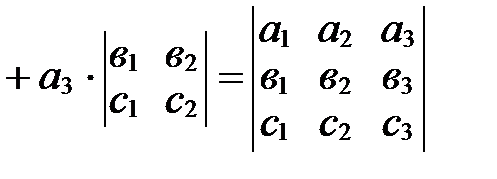 . .
Применение смешанного произведения
Трех векторов
Смешанное произведение векторов применяется:
1. Для выяснения компланарности трех векторов:
векторы  , , 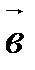 , , 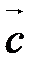 компланарны тогда и только тогда, когда компланарны тогда и только тогда, когда  . .
2. Для вычисления объема параллелепипеда:  (рис. 27). (рис. 27).
3. Для вычисления объема треугольной призмы:
 (рис. 28). (рис. 28).
4. Для вычисления объема тетраэдра (треугольной пирамиды):
 (рис. 29). (рис. 29).
Метод координат
На плоскости и в пространстве
Лекция 7
Аффинная и прямоугольная декартова
Системы координат
Понятие аффинной и прямоугольной декартовой
Систем координат
Четверка, состоящая из точки О и базиса  , ,  , ,  в пространстве, называется аффинной системой координат в пространстве и обозначается в пространстве, называется аффинной системой координат в пространстве и обозначается  или или  (рис. 30). (рис. 30).
Точка О называется началом координат, векторы 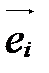 , ,  , - координатными векторами: , - координатными векторами:  - первый координатный вектор, - первый координатный вектор,  - второй, - второй,  - третий. - третий.
Направленные прямые, на которых положительное направление определяется базисными векторами и которые проходят через точку О, называются координатными осями:
 - ось абсцисс; - ось абсцисс;
 - ось ординат; - ось ординат;
 - ось аппликат (рис. 31). - ось аппликат (рис. 31).
Оси абсцисс, ординат и аппликат обозначаются и так: Ох, Оу, Оz.
Плоскости, определяемые осями Ох и Оу, Оу и Оz, Ох и Оz, называются координатными плоскостями и обозначаются Оху, Оуz, Oxz, а систему координат  иногда обозначают Oxyz. иногда обозначают Oxyz.
Пусть  - аффинная система координат, М – произвольная точка пространства. Вектор - аффинная система координат, М – произвольная точка пространства. Вектор  называется радиус-вектором точки М относительно точки О (рис. 32). называется радиус-вектором точки М относительно точки О (рис. 32).
Понятие координат точки вводится на основе понятия координат вектора.
Координатами точки М в системе координат  называются координаты ее радиус-вектора называются координаты ее радиус-вектора  в базисе в базисе  , ,  , ,  . .
Обозначение  или просто М(х;у;z): х – абсцисса точки М, у – ордината, z – аппликата. или просто М(х;у;z): х – абсцисса точки М, у – ордината, z – аппликата.
Если в пространстве задана аффинная система координат, то устанавливается взаимно однозначное соответствие между точками пространства и упорядоченными тройками (х;у;z) действительных чисел.
Рассмотрим особенности расположения точки относительно аффинной системы координат, если некоторые ее координаты являются нулевыми. Пусть М(х;у;z).
1) Если z =0, то М(х;у;0) Þ  Þ Þ  . Верно и обратное: . Верно и обратное:  Þ z =0. Þ z =0.
2) Докажите самостоятельно, что если у=0, то  , и наоборот, если , и наоборот, если  , то у=0. , то у=0.
3) Докажите самостоятельно, что если х=0, то  , и наоборот, если , и наоборот, если  , то х=0. , то х=0.
4) Если z =0 и у=0, то  и и  Þ Þ  Þ Þ  . Верно и обратное: . Верно и обратное:  Þ z =0 и у=0. Þ z =0 и у=0.
Докажите самостоятельно, что:
5) Если х =0 и у=0, то  и наоборот, если и наоборот, если  , то х =0 и у=0. , то х =0 и у=0.
6) Если х =0 и z =0, то  и наоборот, если и наоборот, если  , то х =0 и z =0. , то х =0 и z =0.
7) Так как  , то из пунктов 1) – 3) следует, что О (0;0;0) в системе координат , то из пунктов 1) – 3) следует, что О (0;0;0) в системе координат 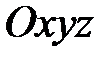 . .
Чтобы построить точку М(х;у;z) по ее координатам в системе координат  , надо сначала построить точку М1 (х;0;0), затем точку М2 (х;у;0), а затем точку М (х;у;z). Процесс построения этих точек показан на рис. 33. Ломаная ОМ1М2М называется координатной ломаной точки М. , надо сначала построить точку М1 (х;0;0), затем точку М2 (х;у;0), а затем точку М (х;у;z). Процесс построения этих точек показан на рис. 33. Ломаная ОМ1М2М называется координатной ломаной точки М.
Система координат называется прямоугольной декартовой, если ее базис является ортонормированным. Обозначение прямоугольной декартовой системы координат:  или или 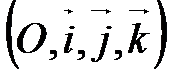 , где , где 
 , ,  , ,  и и  . .
Прямоугольная декартова система координат является частным случаем аффинной.
Замечание. На плоскости аффинная система координат состоит из точки О (начала координат) и двух базисных векторов  и и  (координатных векторов) (рис. 34). Поэтому в системе координат на плоскости любая точка имеет две координаты (координатных векторов) (рис. 34). Поэтому в системе координат на плоскости любая точка имеет две координаты 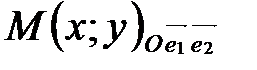 . Прямоугольная декартова система координат на плоскости изображена на рис. 35. . Прямоугольная декартова система координат на плоскости изображена на рис. 35.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|
 и
и  .
.
 ,
,  ,
,  в пространстве, называется аффинной системой координат в пространстве и обозначается
в пространстве, называется аффинной системой координат в пространстве и обозначается  или
или  (рис. 30).
(рис. 30).
 - аффинная система координат, М – произвольная точка пространства. Вектор
- аффинная система координат, М – произвольная точка пространства. Вектор  называется радиус-вектором точки М относительно точки О (рис. 32).
называется радиус-вектором точки М относительно точки О (рис. 32).
 или
или 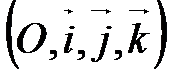 , где
, где 




